Plus Two Maths Chapter Wise Questions and Answers Chapter 2 Inverse Trigonometric Functions are part of Plus Two Maths Chapter Wise Questions and Answers. Here we have given Plus Two Maths Chapter Wise Questions and Answers Chapter 2 Inverse Trigonometric Functions.
| Board | SCERT, Kerala |
| Text Book | NCERT Based |
| Class | Plus Two |
| Subject | Maths Chapter Wise Questions |
| Chapter | Chapter 2 |
| Chapter Name | Inverse Trigonometric Functions |
| Number of Questions Solved | 47 |
| Category | Plus Two Kerala |
Kerala Plus Two Maths Chapter Wise Questions and Answers Chapter 2 Inverse Trigonometric Functions
Plus Two Maths Inverse Trigonometric Functions Three Mark Questions and Answers
Question 1.
Prove the following:

Answer:

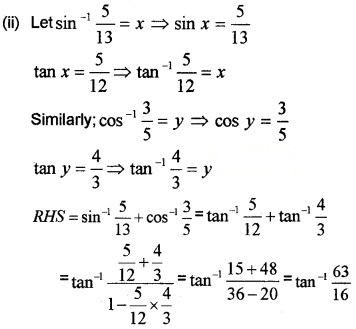
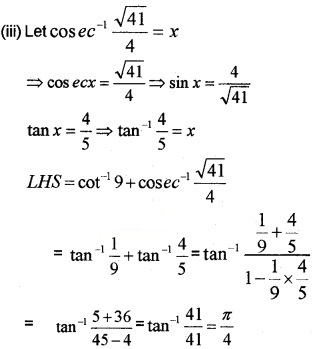
Question 2.
Find the value of
![]()
Answer:

Question 3.
If tan-1x + tan-1y + tan-1z = π, show that x + y + z = xyz
Answer:
Given;
tan-1x + tan-1y + tan-1z = π
⇒ tan-1x + tan-1y = π – tan-1z

⇒ x + y + z = xyz.
Question 4.
Match the following

Answer:

Question 5.
Solve 2 tan-1(cos x) = tan-1(2 cos x)
Answer:
2 tan-1(cosx) = tan-1(2cosx)
⇒ \(\frac{2 \cos x}{1-\cos ^{2} x}\) = 2cosx
⇒ 1 = 1 – cos2 x ⇒ 1 = sin2x
⇒ x = ±\(\frac{\pi}{2}\).
Question 6.
Solve the following
- 2tan-1(cosx) = tan-1(2cosecx)
- tan-12x + tan-13x = \(\frac{\pi}{4}\)
Answer:
1. 2tan-1(cosx) = tan-1(2cosecx)
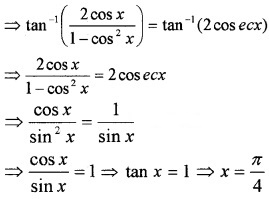
2. tan-12x + tan-13x = \(\frac{\pi}{4}\)
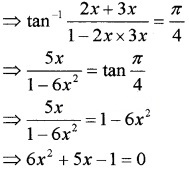
⇒ (6x – 1)(x + 1) = 0
⇒ x = \(\frac{1}{6}\), x = – 1
Since x = – 1 does not satisfy the equation, as the LHS becomes negative. So x = \(\frac{1}{6}\).
Question 7.
Solve 2 tan-1(cos x) = tan-1(2 cos x)
Answer:
2 tan-1(cos x) = tan-1(2 cos x)
⇒ \(\frac{2 \cos x}{1-\cos ^{2} x}\) = 2cosx
⇒ 1 = 1 – cos2 x
⇒ 1 = sin2 x
⇒ x = ±\(\frac{\pi}{2}\)
Plus Two Maths Inverse Trigonometric Functions Four Mark Questions and Answers
Question 1.
Prove that \(\sin ^{-1} \frac{12}{13}+\cos ^{-1} \frac{4}{5}+\tan ^{-1} \frac{63}{16}=\pi\)
Answer:
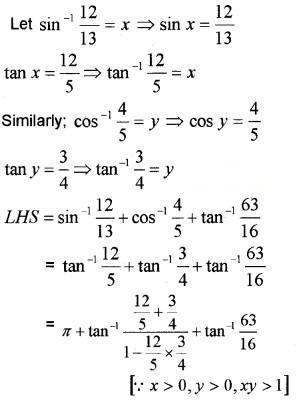
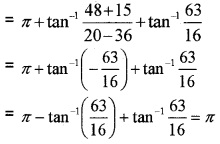
Question 2.
- Find the principal value of sec-1\(\left(-\frac{2}{\sqrt{3}}\right)\) (1)
- if sin\(\left(\sin ^{-1}\left(\frac{1}{5}\right)+\cos ^{-1}(x)\right)=1\), then find the value of x. (3)
Answer:
1. principal value of:
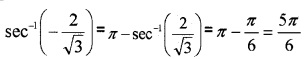
2. find the value of x:
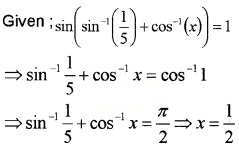
Question 3.
Solve the following
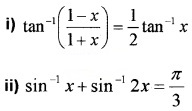
Answer:
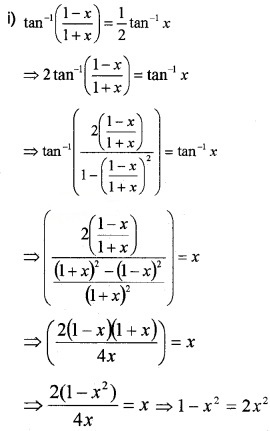
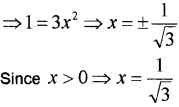
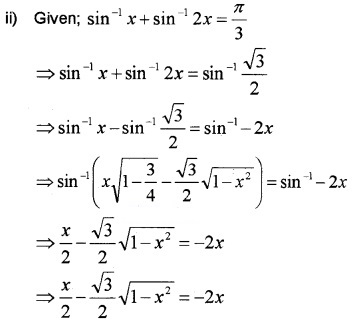
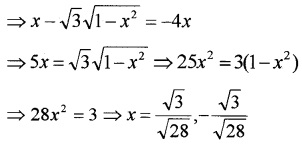
The value x = –\(\frac{\sqrt{3}}{\sqrt{28}}\) makes the LHS negative, so rejected.
Question 4.
(i) Choose the correct answer from the bracket. cos(tan-1 x), |x| < 1 is equal to (1)
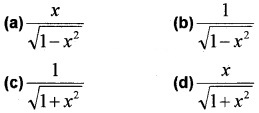
![]()
Answer:
![]()
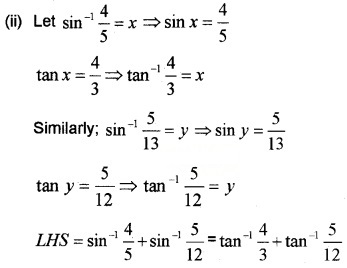
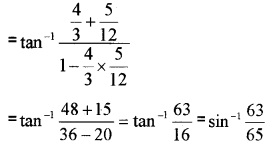
(draw a right triangle to convert ‘tan’ to ‘sin’).
Question 5.
(i) In which quadrants are the graph of cos-1 (x) lies, x ∈ [-1,1 ] (1)
(ii) If cos-1x + cos-1y = \(\frac{\pi}{3}\), then
sin-1x + sin-1y = ……… (3)
(a) \(\frac{2 \pi}{3}\)
(b) \(\frac{\pi}{3}\)
(c) \(\frac{\pi}{6}\)
(d) \(\frac{\pi}\)
(iii) If tan-1x + tan-1y = \(\frac{\pi}{4}\) then prove that x + y + xy = 1 (2)
Answer:
(i) First and Second quadrant

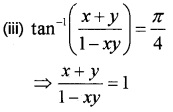
⇒ x + y = 1 – xy ⇒ x + y + xy = 1.
Question 6.
(i) sin(tan-1(1)) is equal to

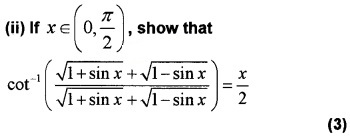
Answer:
![]()
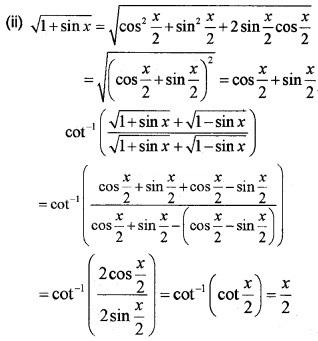
Plus Two Maths Inverse Trigonometric Functions Six Mark Questions and Answers
Question 1.
Show that sin-1\(\frac{3}{5}\) – sin-1\(\frac{8}{17}\) = cos-1\(\frac{84}{85}\).
Answer:
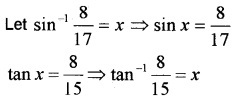
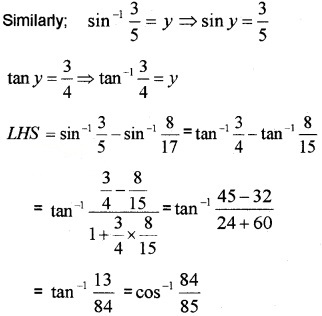
(draw a right triangle to convert ‘tan’ to ‘cos’).
Question 2.
(i) Choose the correct answer from the Bracket.
If cos-1x = y, then y is equal to (1)
(a) π ≤ y ≤ π
(b) 0 ≤ y ≤ π
(c) \(-\frac{\pi}{2}\) ≤ y ≤ \(\frac{\pi}{2}\)
(d) 0 ≤ y ≤ π
(ii) Find the value of cos-1 cos\(\left(\frac{7 \pi}{3}\right)\) (3)
(iii) Solve for x if, tan-1\(\left(\frac{1+x}{1-x}\right)\) = 2 tan-1x (2)
Answer:
(i) Range of cos-1x is [0, π] ⇒ 0 ≤ y ≤ π
(ii) Here \(\left(\frac{7 \pi}{3}\right)\) lie outside the interval [0, π].
To make it in the interval proceed as follows.
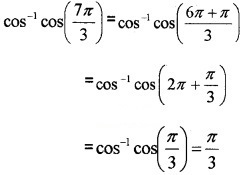
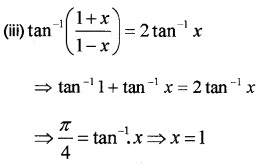
We hope the given Plus Two Maths Chapter Wise Questions and Answers Chapter 2 Inverse Trigonometric Functions will help you. If you have any query regarding Plus Two Maths Chapter Wise Questions and Answers Chapter 2 Inverse Trigonometric Functions, drop a comment below and we will get back to you at the earliest.