Plus Two Maths Chapter Wise Questions and Answers Chapter 1 Relations and Functions are part of Plus Two Maths Chapter Wise Questions and Answers. Here we have given Plus Two Maths Chapter Wise Questions and Answers Chapter 1 Relations and Functions.
| Board | SCERT, Kerala |
| Text Book | NCERT Based |
| Class | Plus Two |
| Subject | Maths Chapter Wise Questions |
| Chapter | Chapter 1 |
| Chapter Name | Relations and Functions |
| Number of Questions Solved | 47 |
| Category | Plus Two Kerala |
Kerala Plus Two Maths Chapter Wise Questions and Answers Chapter 1 Relations and Functions
Plus Two Maths Relations and Functions Three Mark Questions and Answers
Question 1.
Show that the relation R in the set is given by A = {x ∈ Z, 0 = x = 12}
R = {(a,b): a – b is a multiple of 4}
Answer:
Given; R = {(a,b): a – b is a multiple of 4}
Clearly a – a = 0 is a multiple of 4. So
(a, a) ∈ R, hence Reflexive
(a,b) ∈ R ⇒ a -b is a multiple of 4, imply that b – a is a multiple of 4 ⇒ (b, a) ∈ R So Symmetric.
(a, b), (b, c) ∈ R ⇒ a – b and b – c are multiple of 4.
a – b + b – c is a multiple of 4
a – c is a multiple of 4 ⇒ (a, c) ∈ R So Transitive.
Hence R is an equivalence Relation.
Question 2.
Let R be a Relation in the set A = {1, 2, 3, 4, 5, 6} defines as R = {(x,y): y = 2x – 1}
- Write R in roster form and find it’s domain and range
- Is R an equivalence relation ? Justify.
Answer:
1. R ={(1, 1), (2, 3), (3, 5)}
Domain = {1, 2, 3} ; Range ={1, 3, 5}
2. Since (2, 2) ∉ R, R is not reflexive
(2, 3) ∈ R but (3, 2) ∉ R
R is not symmetric.
(2, 3) ∈ R, (3, 5) ∉ R but, (2, 5) ∉ R
R is not transitive
∴ R is not an equivalence relation.
Question 3.

Answer:
Given;
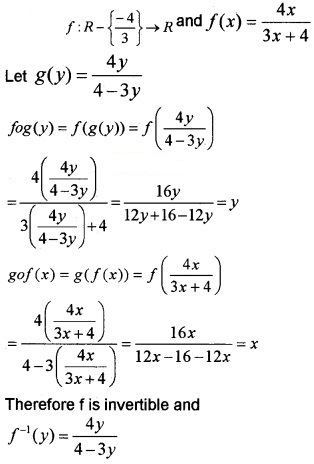
Question 4.
Let ‘ * ’ is a binary operation on the set Q of rational numbers as follows;
- a * b = a – b
- a * b = a + ab
- a * b = a2 + b2
- a * b = (a – b)2
Find which of the binary operation are commutative and associative. Also find the identity element if exists.
Answer:
1. Given; a * b = a – b
b * a = b – a ≠ a – b = a * b
Hence not commutative.
Now; a * (b * c) = a * (b – c)
= a – (b – c) – a – b + c
(a * b) * c = (a – b) * c = a – b – c
a * (b * c) ≠ (a * b) * c
Hence not associative.
Now; a * e = a ⇒ a – e = a ⇒ e = 0
e * a = a ⇒ e – a = a ⇒ e = 2a
a * e ≠ e * a.
So identity element does not exist.
2. Given; a * b = a + ab
b * a = b + ab ≠ a + ab = a * b
Hence not commutative.
Now; a * (b * c) = a * (b + bc)
= a + a(b + be) = a + ab + abc
(a * b) * c = (a + ab) * c
= a + ab + c(a + ab)
= a + ab + ac + abc
a * (b * c) * (a * b) * c
Hence not associative.
Now; a * e = a ⇒ a + ae = a ⇒ e = 0
e * a = a ⇒ e + ea = a ⇒ e = \(\frac{a}{1+a}\)
a * e ≠ e * a.
So identity element does not exist.
3. Given; a * b = a2 + b2
b * a = b2 + a2 = a2 + b2 = a * b
Hence commutative.
Now; a * (b * c) = a* (b2 + c2) = a2 + (b2 + c2)2
(a * b) * c = (a2 + b2) * c
= (a2 + b2)2 + c2
a * (b * c) ≠ (a * b) * c
Hence not associative.
Now; a * e – a ⇒ a2 + e2 = a
⇒ e = \(\sqrt{a-a^{2}}\) ∉ Q
So identity element does not exist.
4. Given; a * b = (a – b)2
b * a = (b – a)2 = (a – b)2 = a * b
Hence commutative.
Now; a * (b * c) = a * (b – c)2 (a – (b-c)2)2
(a * b) * c – (a – b)2 * c = ((a – b)2 – c)2
a * (b * c) ≠ (a * b) * c
Hence not associative.
Now; a * e = \(\sqrt{a}\) ⇒ e = a – \(\sqrt{a}\) ∉ Q
So identity element does not exist.
Question 5.
Show that the relation R on the set of natural numbers defined as R: { (x, y): y – x is a multiple of 2} is an equivalance relation
Answer:
Since x – x = 0 is multiple of 2, (x, x)∈ R
Therefore reflexive.
If y – x is a multiple of 2 then x – y is also a multiple of 2. Therefore (x, y) ∈ R ⇒ (y, x) ∈ R. Hence symmetric.
If y – x is a multiple of 2 and z-y is a multiple of 2, then their sum y – x + z – y = z – x is a multiple of 2. Therefore (x, y), (y, z) ∈ R ⇒ (x, z) ∈ R
Hence transitive.
Therefore R is an equivalance relation.
Question 6.
Consider f : [3, ∞) → [1, ∞) given by f(x) = x2 – 6x + 10. Find f-1
Answer:
f(x) = (x – 3)2 + 1
y = (x – 3)2 + 1
⇒ (x – 3)2 = y – 1
⇒ x = \(\sqrt{y-1}\) + 3
∴ f-1(x) = \(\sqrt{x-1}\) + 3
Question 7.
‘*’ be a binary operation on N × N defined as (a, b) * (c, d) – (ac, bd)
- Show that * is commutative.
- Find the identity element of * if any
- Write an element of N × N which has an inverse.
Answer:
1. (a, b) * (c, d) = (ac, bd) = (ca, db)
= (c, d) * (a, b)
Hence * is commutative.
2. (a, b) * (e, e) = (a, b)
⇒ (ae, be) = (a, b)
⇒ ae = a ⇒ e = 1
⇒ be = b ⇒ e = 1
Therefore (1,1) is the identity element.
3. Invertible element is (1,1).
Question 8.
Show that the relation R in the set R of Real numbers defined asR = {(a, b): a ≤ b2} is neither reflexive, nor symmetric nor transitive.
Answer:
a ≤ a2 is not true for all a. So (a, a) ∉ R hence not Reflexive.
(a, b) ∈ R ⇒ a ≤ b2 does not imply that b ≤ a2. So (b, a) ∉ R, hence not Symmetric. (a, b),(b, c) ∈ R ⇒ a ≤ b2 and b ≤ c2 does not imply that a ≤ c2. So (a, c) ∉ R, hence not Transitive.
Question 9.
Consider f :R+ → [-5, ∞) given by f(x) = 9x2 + 6x – 5. Show that fis invertible with f-1(y) = \(\frac{\sqrt{y+6}-1}{3}\)
Answer:

f is invertible and f-1(y) = \(\frac{\sqrt{y+6}-1}{3}\).
Question 10.
Let A = R – {3} and B = R – {1} consider the function f: A → B defined by f(x) = \(\frac{x-2}{x-3}\) is f one-one and onto? Justify your answer.
Answer:
Given; f: A → B, A = R – {3} and B = R – {1}
f(x1) = f(x2) ⇒ \(\frac{x_{1}-2}{x_{1}-3}=\frac{x_{2}-2}{x_{2}-3}\)
⇒ (x1 – 2)(x2 – 3) = (x2 – 2)(x1 – 3)
⇒ x1x2 – 2x2 – 3x1 + 6 = x2x1 – 2x1 – 3x2 + 6
⇒ -2x2 – 3x1 = – 2x1 – 3x2 ⇒ x1 = x2
Hence one-one
Let y ∈ B ⇒ f(x) = y ⇒ \(\frac{x-2}{x-3}\) = y
⇒ x – 2 = xy – 3y
⇒ x – xy = 2 – 3y
⇒ x(1 – y) = 2 – 3y ⇒ x = \(\frac{2-3 y}{1-y}\) ∈ A=
Hence onto. Therefore bijective.
Question 11.

Answer:
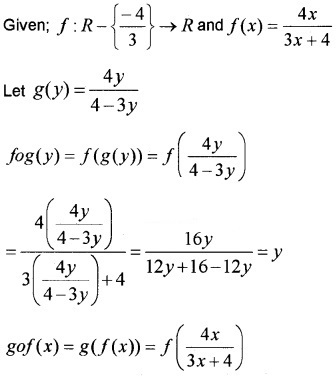

Plus Two Maths Relations and Functions Four Mark Questions and Answers
Question 1.
The relation R defined in the set A = {-1, 0, 1} as R = {(a,b):a = b2}
- Check whether R is reflexive, symmetric and transitive.
- Is R an equivalence relation
Answer:
1. (-1, -1) ∉ R, R is not reflexive
(-1,1) ∈ R but (1, -1) ∉ R, R is not symmetric
(-1,1) ∈ R, (1, 1) ∈ R and (-1, 1) ∈ R,
R is transitive.
2. R is not reflexive, not symmetric, and not transitive. So R is not an equivalence relation.
Question 2.
Let A = {1, 2, 3}. Give an example of relation on A which is
- Symmetric but neither reflexive nor transitive.
- Transitive but neither reflexive nor symmetric.
Answer:
1. R = {(1, 2),(2, 1)}
(1, 1) ∉ R ⇒ R is not reflexive
(1, 2) ∈ R ⇒ (2, 1) ∈ R, R is symmetric
(1, 2) ∈ R, (2, 1) ∈ R but (1,1) ∉ R,
R is not transitive
2. R = {(1, 2),(1, 3),(2, 3)}
(1, 1) ∉ R ⇒ R is not reflexive
(1, 2) ∈ R ⇒ but (2,1) ∉ R, R is not symmetric
(1, 2) ∈ R, (2, 3) ∈R ⇒ (1, 3) ∈ R,
R is transitive.
Question 3.
Find fog and gof if
- f(x) – |x| and g(x) – |3x + 4|
- f(x) = 16x4 and g(x) = x \(\frac{1}{4}\)
Answer:
1. Given; f(x) = |x| and g(x) = |3x + 4|
fog(x) = f(g(x))
= f(|3x + 4|) = ||3x + 4|| = |3x + 4|
gof(x) = g(f(x)) = g(|x|) = |3|x| + 4|
2. fog(x) = f(g(x)) = g(x\(\frac{1}{4}\)) = 16(x\(\frac{1}{4}\))4 = x
gof (x) = g(f(x)) = g(16x4) = (16x4)\(\frac{1}{4}\) = 4x.
Question 4.
Consider the binary operation* : Q → Q where Q is the set of rational numbers is defined as a * b = a + b – ab
- Find 2 * 3 (1)
- Is identity for * exist? If yes, find the identity element. (2)
- Are elements of Q invertible? Is yes, find the inverse of an element in Q (1)
Answer:
1. 2 * 3 = 2 + 3 – 6 = -1.
2. a * e = a ⇒ a + e – ae = a
⇒ e(1 – a) – 0 ⇒ e = 0
e * a = a ⇒ e + a – ea = a
⇒ e(1 – a) = 0 ⇒ e = 0 is the identity element.
3. a * b = 0 ⇒ a + b – ab = 0 ⇒ b = \(\frac{a}{a-1}\)
Question 5.
‘*’ is a binary operation on R defined as a * b = 2ab
- Determine whether * is commutative and associative
- Find the identity element if exists.
- Find the inverse element, if exists
Answer:
1. a * b = 2ab = 2ba = b * a
Therefore commutative
a * (b * c) = a * (2bc) = 4abc
(a * b) * c = (2ab) * c = 4 abc
Therefore is associative.
2. a * e = a ⇒ 2ae = a ⇒ e = \(\frac{1}{2}\)
e * a = a ⇒ 2ea = a ⇒ e = \(\frac{1}{2}\)
Therefore identity element is \(\frac{1}{2}\).
3. a * b = \(\frac{1}{2}\) ⇒ 2ab = \(\frac{1}{2}\) ⇒ b = \(\frac{1}{4a}\), a ≠ 0.
Question 6.
- If f: R – {2} → R – {2}, defined by f(x) = \(\frac{2 x-3}{x-2}\) then find fof
- Which of the following satisfies the condition f-1 ≠ f.
(a) f : R – {0} → R – {0}, f(x) = \(\frac{1}{x}\)
(b) f :R → R, f(x) = -x
(c) f : R – {-1} → R – {-1}, f(x) = \(\frac{x}{x+1}\)
(d) f: R – {2} → R – {2}, f(x) = \(\frac{2 x-3}{x-2}\)
Answer:
1. fof(x) = f(f(x)) = f\(\left(\frac{2 x-3}{x-2}\right)\)

2. Following satisfies the condition f-1 ≠ f:
(a) f : R – {0} → R – {0}, f(x) = \(\frac{1}{x}\)
(b) f :R → R, f(x) = -x
The graph of functions in (a) and (b) symmetric with respect to the line y = x.
The function in (d) we have already shown that fof (x) = x.
So the answer is (c)
f : R – {-1} → R – {-1}, f(x) = \(\frac{x}{x+1}\).
Question 7.
If f :R → R is a function defined by f(x) = 3x – 2
- Show that f is one-one.
- Find fof(x).
- Find the inverse of f if exists.
Answer:
1. f(x1) = f(x2)
⇒ 2x1 – 3 = 2x2 – 3 ⇒ x1 = x2
Therefore one-one.
2. fof(x) = f(f(x)) = f(3x – 2)
f (x) = 3(3x – 2) – 2 = 9x – 6 – 2 = 9x – 8.
3. Let g(x) = \(\frac{x+2}{3}\)
fog(x) = f(g(x))
= f\(\left(\frac{x+2}{3}\right)\) = 3\(\left(\frac{x+2}{3}\right)\) – 2 = x
Similarly we can show that
gof(x) = g(f(x)) = x
Therefore; f-1 = \(\frac{x+2}{3}\).
Question 8.
Let A = N × N and be the binary operation. On A defined by (a, b) * (c, d) = (a+c, b+d). Show that ‘ * ’ is commutative and associative. Find the identity for ‘ * ’ on A if any.
Answer:
Given; A = N × N and
(a, b) * (c, d) = (a + c, b + d)
(c, d) * (a, b) = (c + a, d + b)
= (a + c, b + d) = (a, b) * (c, d))
Hence commutative.
Now; (a, b) * [(c, d) * (e, f)] = (a, b) * [c + e, d+f]
= (a + c + e, b + d + f)
[(a, b) * (c, d)] * (e, f) = [a + c, b + d] * (e, f)
= (a + c + e, b + d + f)
Hence associative.
(a, b) * (e, e) = (a, b) ⇒ (a + e, b + e) = (a, b)
⇒ a + e = a, b + e = b ⇒ e=0, e = 0 ⇒ (0,0) ∉ A
So identity element does not exist.
Question 9.
If f(x) = \(\left(\frac{4x+3}{6x-4}\right)\), x ≠ \(\frac{2}{3}\)
- Show that fof{x)=x, for all x ≠ \(\frac{2}{3}\).
- What is the inverse of ‘f?
Answer:
1.
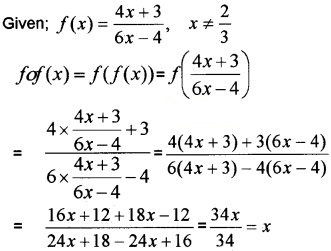
2. Since; fof(x) = x
f is the inverse of itself.
Question 10.
1. Let f be a function defined by f(x) = \(\sqrt{x}\) is a function if it defined from (1)
(a) f : N → N
(b) f : R → R
(c) f : R → R+
(d) f : R+ → R+
2. Check the injectivity and surjectivity of the following functions (3)
(a) f : N → N defined by f(x) = x3
(b) f : R → R given by f(x) = [x]
Answer:
1.
(d) f : R+ → R+
2.
(a) For x, y ∈ N,
f(x) = f(y) ⇒ x3 = y3 ⇒ x = y
Therefore, f is injective
For 2 ∈ N, there does not exist x in the domain N such that f(x) = x3 = 2.
∴ f is not surjective.
(b) f : R → R given by f(x) = [x]
It seen that f(1.1) = 1 and f(1.8) = 1;
But 1.1 ≠ 1.8;
∴ f is not injective
There does not exist any element x ∈ R
such that f(x) = 0.7
∴ f is not surjective.
Plus Two Maths Relations and Functions Six Mark Questions and Answers
Question 1.
Consider the function f(x) \(=\frac{x+1}{x-1}\); x ≠ 1
1. fof(2) = ____
(a) 1
(b) 2
(c) 3
(d) 4
2. What is the inverse of f?
3. f(3) + f-1(3)
Answer:
1. fof(2):
(b) 2

2. Let g : range of f → R- {1} inverse of f Let ‘y be any arbitrary element in the range of f
then y = f(x) = \(\frac{x+1}{x-1}\)
⇒ xy – y = x + 1 ⇒ x(y – 1) = y +1
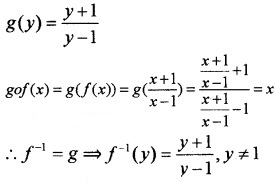
Let us defi ne g : range of f → R- {1} as
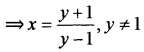
3. f(3) = 2, f-1(3) = 2
f(3) + f-1(3) = 2 + 2 = 4.
Question 2.
1. Show that the function f: R → R defined by f(x) = 2x – 3 is one-one and onto. Find f-1
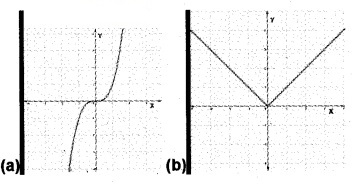
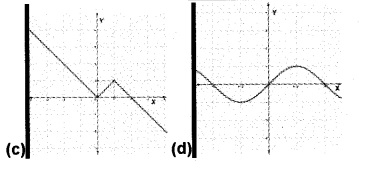
2. Which of the following figure represents the graph of a function on R which is onto but not one-one.
3. Write a function on R which is onto but not one-one
Answer:
1. f(x) = 2x – 3
f(x1) = f(x2)
⇒ 2x1 – 3 = 2x2 – 3 ⇒ x1 = x2
Therefore f is one-one.
Let f(x) = yeR, then
y = 2x – 3 ⇒ 2x = y + 3 ⇒ x = \(\frac{y+3}{2}\) ∈ R
Therefore f is onto. Then f-1(x) = \(\frac{x+3}{2}\).
2. Option (c)
[(b),(c),(d) are not one-one since for different values of x, we have the same value of y. ie; horizontal line meets at more than one point, (b) and (d) are not onto since range and codomain are different].
3. f(x) = x2, f : R → [0, ∞) (Any other function).
Question 3.
A = {1, 2, 3, 4, 6}, * is a binary operation on A is defined as a * b = HCF of a and b.
- Represent * with the help of an operating table.
- Find the identity element.
- Write a commutative binary operation on A with 3 as the identity element. (Hint: Operation table may be used.
Answer:
1.
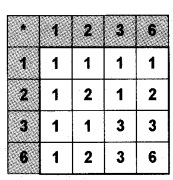
2. From the table it is clear that the identity element is 6.
3. We can write any operation table which is commutative with 3 as the identity element.
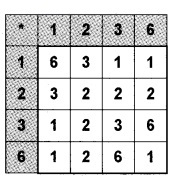
Question 4.
Let * be a binary operation on the set of all real numbers R defined by a * b = a + b + a2b for a, b R.
- Find 2 * 6 and 6 * 2. (2)
- Prove that * is neither commutative nor associative. (2)
- Find the identity elements in R if exists. (2)
Answer:
1. a * b = a + b + a2b
2 * 6 = 2 + 6 + 22 × 6 = 8 + 24 = 32
6 * 2 = 6 + 2 + 62 × 2 = 8 + 72 = 80.
2. a * b = a + b + a2b a * b ≠ b * a
b * a = b + a + b2a
∴ is not commutative.
(ab)c = (a + b + a2b) c
= a + b + a2b + c + (a + b + a2b)2c
a * (b * c) = a * (b + c + b2c)
= a + b + c + b2c + a2(b + c + b2c)
∴ is not associative.
3. Let e is the identity element.
∴ a * e = a ⇒ a + e + a2e = a ⇒ e(1 + a2) = 0
∴ e = 0
∴ e * a = a ⇒ e + a + e2a = a ⇒ e + e2a = 0
⇒ e(1 + ae) = 0
⇒ e = 0; (1 + ae) = 0
ea = -1 ⇒ e = – \(\frac{1}{a}\)
Identity element does not exists.
Question 5.
- Consider f: {3, 4, 5, 6} → {8, 10, 12, 13, 14} And f = { (3, 8), (4, 10), (5, 12), (6, 14)}. State whether f has inverse ? Give reason. (2)
- Consider f : R → R given by f(x) = 3x + 2 Show that f is invertible. Find the inverse of f
Answer:
1. Distinct elements in set {3, 4, 5, 6} has distinct images, under f.
∴ f is one- one
But 14 in the codomain has no pre-image.
∴ f is not onto.
∴ f has no inverse.
2. f(x) = 3x + 2; then
f(x1) = f(x2) = 3x2 + 2 ⇒ x1= x2
Hence F is one – one
For y ∈ R, let y = 3x + 2 ⇒ x = \(\frac{y-2}{3}\) ∈ R

We hope the given Plus Two Maths Chapter Wise Questions and Answers Chapter 1 Relations and Functions will help you. If you have any query regarding Plus Two Maths Chapter Wise Questions and Answers Chapter 1 Relations and Functions, drop a comment below and we will get back to you at the earliest.