Percents
Percents are used to describe parts of a whole base amount. When one of the parts of the relationship is unknown, we can solve an algebraic equation for the unknown quantity.
(The solution methods shown on this page are of an algebraic, sentence translation nature. Of course, other methods of solution are also possible.)
There are two main types of problems dealing with percents:
1. In the first type of problem, the percent is given.
In these problems, you will change the percent to a decimal.
To change a percent to a decimal, divide the number by 100.
This will move the decimal point two places to the left.
Example 1: Find 7% of 250.
(This can also be read “What number is 7% of 250?”)
Solution: Let x = the answer
x = 7% • 250
x = 0.07 • 250 changing 7% to a decimal
x = 17.5
Remember that the word “of ” means to multiply!
Example 2: 30 is 15% of what number?
Solution: Let n = the answer (“what number”)
30 = 15% • n
30 = 0.15 • n changing 15% to a decimal
30/0.15 = n dividing both sides by 0.15
200 = n
n = 200
Remember that the word “of ” means to multiply!
2. In the second type of problem, you are looking for the percent.
In these problems, you will represent the % as a fraction.
Example 1: 3 is what percent of 12?
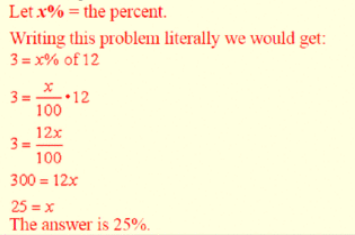
To change a percent to a fraction, divide the percent value by 100.
Application Problems
Example 1: If 120 million roses were sold on Valentine’s Day, and 75% of the roses were red, how many red roses were sold on Valentine’s Day?
Solution: Let x = the number of red roses sold
x = 75% of 120
x = 0.75 • 120
x = 90 million red roses sold
Example 2: Juan missed 6 out of 92 questions on a test. To the nearest percent, what percent of the questions did he solve correctly?
Solution:
If he missed 6 questions, he got 86 questions correct.
∴ 86 is what percent of 92
86 = x% of 92
⇒ 86 = \(\frac { x }{ 100 } \) • 92
⇒ 86 = \(\frac { 92x }{ 100 } \)
⇒ 8600 = 92x
⇒ x = 93.47
To the nearest percent, he got 93% correct.