NCERT Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.2 are part of NCERT Solutions for Class 10 Maths. Here are we have given Chapter 6 Triangles Class 10 NCERT Solutions Ex 6.2.
- Triangles Class 10 Ex 6.1
- Triangles Class 10 Ex 6.3
- Triangles Class 10 Ex 6.4
- Triangles Class 10 Ex 6.5
- Triangles Class 10 Ex 6.6
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 6 |
| Chapter Name | Triangles |
| Exercise | Ex 6.2 |
| Number of Questions Solved | 10 |
| Category | NCERT Solutions |
NCERT Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.2
NCERT Solutions for Class 10 Maths
Page No: 128
Question 1. (i) and (ii), DE || BC. Find EC in (i) and AD in (ii).
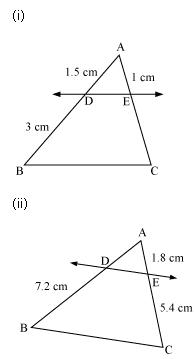
Solution:
(i)

Let EC = x
Since DE || BC.
Therefore, by basic proportionality theorem,

(ii)
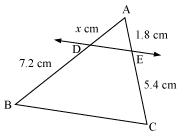
Let AD = x
Since DE || BC,
Therefore by basic proportionality theorem,

Question 2. E and F are points on the sides PQ and PR respectively of a ΔPQR.
For each of the following cases, state whether EF || QR.
(i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm
(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm
(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.63 cm
Solution:
(i)
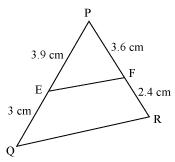
Given that PE = 3.9, EQ = 3, PF = 3.6, FR = 2.4
Now,

(ii)
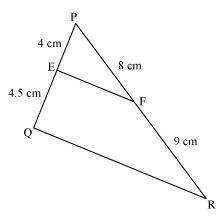
PE = 4, QE = 4.5, PF = 8, RF = 9

(iii)
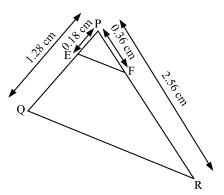
PQ = 1.28, PR = 2.56, PE = 0.18, PF = 0.36

Question 3. In the fig 6.18, if LM || CB and LN || CD, prove that
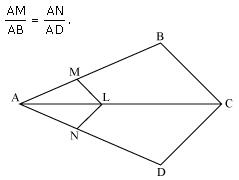
Solution:
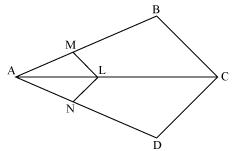
In the given figure
Since LM || CB,
Therefore by basic proportionality theorem,

Question 4. In figure , DE || AC and DF || AE. Prove that
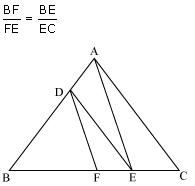
Solution:
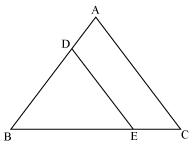
In ∆ABC,
Since DE || AC

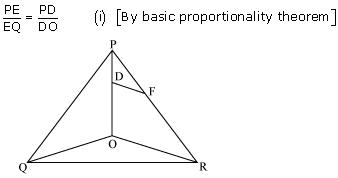
Question 5. In figure , DE || OQ and DF || OR, show that EF || QR.
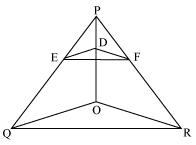
Solution:
In ∆POQ
Since DE || OQ

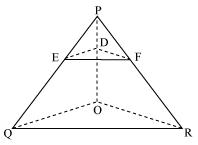
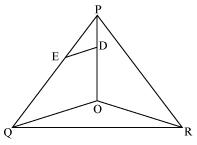
Question 6. In the figure, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.
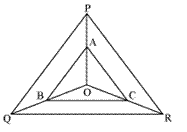
Solution:
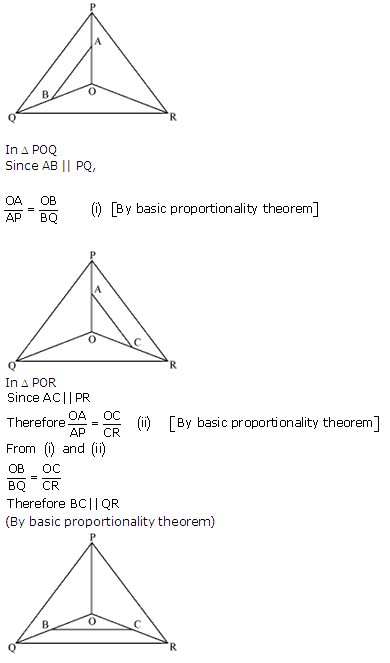
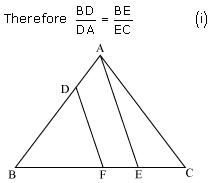
Question 7. Using Basic proportionality theorem, prove that a line drawn through the mid-points of one side of a triangle parallel to another side bisects the third side. (Recall that you have proved it in Class IX).
Solution:
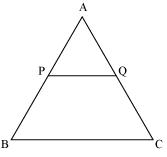
Consider the given figure
PQ is a line segment drawn through midpoint P of line AB such that PQ||BC
i.e. AP = PB
Now, by basic proportionality theorem
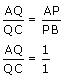
i.e. AQ = QC
Or, Q is midpoint of AC.
Question 8. Using Converse of basic proportionality theorem, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side. (Recall that you have done it in Class IX).
Solution:
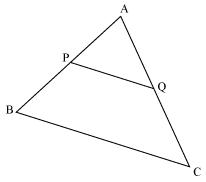
Consider the given figure
PQ is a line segment joining midpoints P and Q of line AB and AC respectively.
i.e. AP = PB and AQ = QC
Now, we may observe that
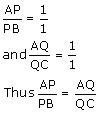
And hence basic proportionality theorem is verified
So, PQ||BC
Question 9. ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O.
Show that \(\frac { AO }{ BO } =\frac { CO }{ DO } \)
Solution:

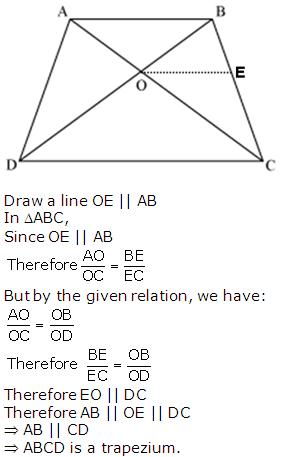
Question 10. The diagonals of a quadrilateral ABCD intersect each other at the point O such that \(\frac { AO }{ BO } =\frac { CO }{ DO } \). Show that ABCD is a trapezium.
Solution:
We hope the NCERT Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.2 help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.2, drop a comment below and we will get back to you at the earliest.