NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.4 are part of NCERT Solutions for Class 10 Maths. Here are we have given Chapter 2 Polynomials Class 10 NCERT Solutions Ex 2.4.
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 2 |
| Chapter Name | Polynomials |
| Exercise | Ex 2.4 |
| Number of Questions Solved | 5 |
| Category | NCERT Solutions |
NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.4
Question 1.Verify that the numbers given alongside of the cubic polynomials below are their zeroes. Also, verify the relationship between the zeroes and the coefficients in each case:
![]()
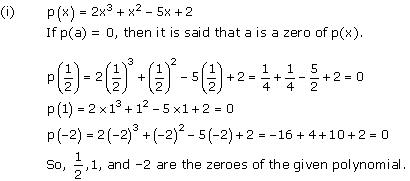
On comparing the given polynomial with the polynomial ax3 + bx2 + cx + d, we obtain a = 2, b = 1, c = -5, d = 2

Thus, the relationship between the zeroes and the coefficients is verified.
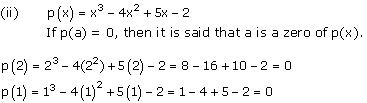
On comparing the given polynomial with the polynomial ax3 + bx2 + cx + d, we obtain a = 1, b = -4, c = 5, d = -2.

Thus, the relationship between the zeroes and the coefficients is verified.
Concept Insight: The zero of a polynomial is that value of the variable which makes the polynomial 0. Remember that there are three relationships between the zeroes of a cubic polynomial and its coefficients which involve the sum of zeroes, product of all zeroes and the product of zeroes taken two at a time.
Question 2. Find a cubic polynomial with the sum, sum of the product of its zeroes taken two at a time, and the product of its zeroes as 2, -7, -14 respectively.
Let the polynomial be ax3 + bx2 + cx + d and its zeroes be α, β, γ.
According to the given information:
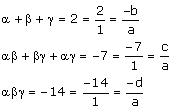
If a = k, then b = -2k, c = -7k, d = 14k
Thus, the required cubic polynomial is k(x3 – 2x2 – 7x + 14), where k is any real number.
The simplest polynomial will be obtained by taking k = 1.
Concept Insight: A cubic polynomial involves four unknowns and we have three relations involving these unknowns, so the coefficients of the cubic polynomial can be found by assuming the value of one unknown and then finding the other three unknowns from the three relations.
Question 3. If the zeroes of the polynomial x3 – 3x2 + x + 1 are a – b, a, a + b, find a and b.
Let p(x) = x3 – 3x2 + x + 1
The zeroes of the polynomial p(x) are given as a – b, a, a + b.
Comparing the given polynomial with dx3 + ex2 + fx + g, we can observe that
d = 1, e = -3, f = 1, g = 1
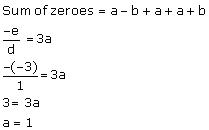
Therefore, the zeroes of p(x) are 1-b, 1, 1+b .
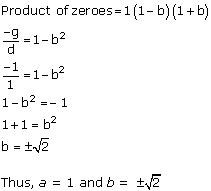
Concept Insight: When the polynomial and its zeroes are given then, remember to apply relationships between the zeroes and coefficients. These relations involve the sum of the zeroes, product of zeroes and the product of zeroes taken two at a time.
Question 4. If two zeroes of the polynomial x4 – 6x3 – 26x2 + 138x – 35 are 2 ±√3, find other zeroes.
Therefore, x2 – 4x + 1 is a factor of the given polynomial. For finding the remaining zeroes of the given polynomial, we will carry out the division of

Hence, 7 and -5 are also zeroes of the given polynomial.
Concept Insight: If a is a zero of a polynomial p(x), where degree of p(x) is greater than 1, then (x – a) will be a factor of p(x) that is when p(x) is divided by (x – a), then the remainder obtained will be 0 and the quotient will be a factor of p(x) using division algorithm. Remember that if (x – a) and (x – b) are factors of a polynomial, then (x – a)(x – b) will also be a factor of that polynomial.
Question 5. If the polynomial x4 – 6x3 + 16x2 – 25x + 10 is divided by another polynomial x2 – 2x + k, the remainder comes out to be x + a, find k and a.
By division algorithm,
Dividend = Divisor x Quotient + Remainder
Divisor x Quotient = Dividend – Remainder
It will be perfectly divisible by x2 – 2x + k.

10 – a – 8 x 5 + 25 = 0
10 – a – 40 + 25 = 0
– 5 – a = 0
a = -5
Thus, k = 5 and a = -5.
Concept Insight: When a polynomial is divided by any non-zero polynomial, then it satisfies the division algorithm which is as below:
Dividend = Divisor x Quotient + Remainder
Divisor x Quotient = Dividend – Remainder
So, from this relation, it can be said that the result (Dividend – Remainder) will be completely divisible by the divisor.
We hope the NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.4 help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.4, drop a comment below and we will get back to you at the earliest.