NCERT Maths Solutions for Ex 2.3 class 10 Polynomials is the perfect guide to boost up your preparation during CBSE 10th Class Maths Examination.
NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.3 are part of NCERT Solutions for Class 10 Maths. Here are we have given Chapter 2 Polynomials Class 10 NCERT Solutions Ex 2.3.
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 2 |
| Chapter Name | Polynomials |
| Exercise | Ex 2.3 |
| Number of Questions Solved | 5 |
| Category | NCERT Solutions |
NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.3
Page No: 36
Question 1. Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following:
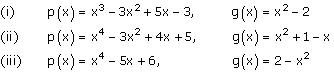

Quotient = x – 3
Remainder = 7x – 9

Quotient = x2 + x – 3
Remainder = 8
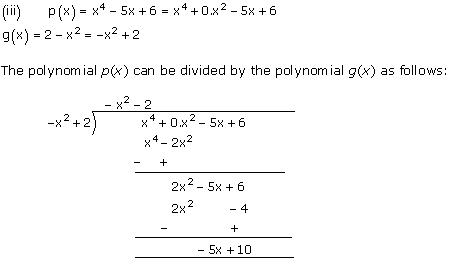
Quotient = -x2 – 2
Remainder = -5x + 10
Concept Insight: While dividing one polynomial by another, first arrange the polynomial in descending powers of the variable. In the process of division, be careful about the signs of the coefficients of the terms of the polynomials. After performing division, one can check his/her answer obtained by the division algorithm which is as below:
Dividend = Divisor x Quotient + Remainder
Also, remember that the quotient obtained is a polynomial only.
Question 2. Check whether the first polynomial is a factor of the second polynomial by dividing the
second polynomial by the first polynomial:
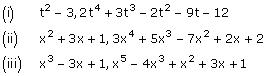
Solution:
The polynomial 2t4 + 3t3 – 2t2 – 9t – 12 can be divided by the polynomial t2 – 3 = t2 + 0.t – 3 as follows:
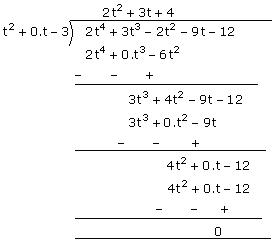
Since the remainder is 0, t² – 3 is a factor of 2t4 + 3t3 – 2t2 – 9t – 12 .
(ii) The polynomial 3x4 + 5x3 – 7x2 + 2x + 2 can be divided by the polynomial x2 + 3x + 1 as follows:
Since the remainder is 0, x² + 3x + 1 is a factor of 3x4 + 5x3 – 7x2 + 2x + 2
(iii) The polynomial x5 – 4x3 + x2 + 3x + 1 can be divided by the polynomial x3 – 3x + 1 as follows:
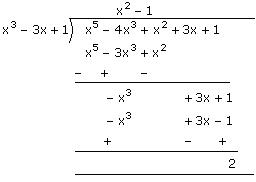
Since the remainder is not equal to 0, x3 – 3x + 1 is not a factor of x5 – 4x3 + x2 + 3x + 1.
Concept Insight: A polynomial g(x) is a factor of another polynomial p(x) if the remainder obtained on dividing p(x) by g(x) is zero and not just a constant. While changing the sign, make sure you do not change the sign of the terms which were not involved in the previous operation. For example in the first step of (iii), do not change the sign of 3x + 1.
Question 3. Obtain all other zeroes of 3x4 + 6x3 – 2x2 – 10x – 5, if two of its zeroes are √(5/3) and – √(5/3).
Solution:
Let p(x) = 3x4 + 6x3 – 2x2 – 10x -5

Now, x² + 2x + 1 = (x + 1)2
So, the two zeroes of x² + 2x + 1 are -1 and -1.
![]()
Concept Insight: Remember that if (x – a) and (x – b) are factors of a polynomial, then (x – a)(x – b) will also be a factor of that polynomial. Also, if a is a zero of a polynomial p(x), where degree of p(x) is greater than 1, then (x – a) will be a factor of p(x), that is when p(x) is divided by (x – a), then the remainder obtained will be 0 and the quotient will be a factor of the polynomial p(x). To cross check your answer number of zeroes of the polynomial will be less than or equal to the degree of the polynomial.
Question 4. On dividing x3 – 3x2 + x + 2 by a polynomial g(x), the quotient and remainder were x – 2 and
-2x + 4, respectively. Find g(x).
Solution:
Divided, p(x) = x3 – 3x2 + x + 2
Quotient = (x – 2)
Remainder = (-2x + 4)
Let g(x) be the divisor.
According to the division algorithm,
Dividend = Divisor x Quotient + Remainder

Concept Insight: When a polynomial is divided by any other non-zero polynomial, then it satisfies the division algorithm which is as below:
Dividend = Divisor x Quotient + Remainder
Divisor x Quotient = Dividend – Remainder
So, from this relation, the divisor can be obtained by dividing the result of (Dividend – Remainder) by the quotient.
Question 5. Give examples of polynomial p(x), g(x), q(x) and r(x), which satisfy the division algorithm and
(i) deg p(x) = deg q(x)
(ii) deg q(x) = deg r(x)
(iii) deg r(x) = 0
Solution:
According to the division algorithm, if p(x) and g(x) are two polynomials with g(x) ≠ 0, then we can find polynomials q(x) and r(x) such that
p(x) = g(x) x q(x) + r(x), where r(x) = 0 or degree of r(x) < degree of g(x).
(i) Degree of quotient will be equal to degree of dividend when divisor is constant.
Let us consider the division of 18x2 + 3x + 9 by 3.
Here, p(x) = 18x2 + 3x + 9 and g(x) = 3
q(x) = 6x2 + x + 3 and r(x) = 0
Here, degree of p(x) and q(x) is the same which is 2.
Checking:
p(x) = g(x) x q(x) + r(x)
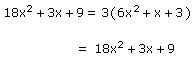
Thus, the division algorithm is satisfied.
(ii) Let us consider the division of 2x4 + 2x by 2x3,
Here, p(x) = 2x4 + 2x and g(x) = 2x3
q(x) = x and r(x) = 2x
Clearly, the degree of q(x) and r(x) is the same which is 1.
Checking,
p(x) = g(x) x q(x) + r(x)
2x4 + 2x = (2x3 ) x x + 2x
2x4 + 2x = 2x4 + 2x
Thus, the division algorithm is satisfied.
(iii) Degree of remainder will be 0 when remainder obtained on division is a constant.
Let us consider the division of 10x3 + 3 by 5x2.
Here, p(x) = 10x3 + 3 and g(x) = 5x2
q(x) = 2x and r(x) = 3
Clearly, the degree of r(x) is 0.
Checking:
p(x) = g(x) x q(x) + r(x)
10x3 + 3 = (5x2 ) x 2x + 3
10x3 + 3 = 10x3 + 3
Thus, the division algorithm is satisfied.
Concept Insight: In order to answer such type of questions, one should remember the division algorithm. Also, remember the condition on the remainder polynomial r(x). The polynomial r(x) is either 0 or its degree is strictly less than g(x). The answer may not be unique in all the cases because there can be multiple polynomials which satisfy the given conditions.
We hope the NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.3 help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.3, drop a comment below and we will get back to you at the earliest.