NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.2 are part of NCERT Solutions for Class 10 Maths. Here are we have given Chapter 1 Real Numbers Class 10 NCERT Solutions Ex 1.2.
- Real Numbers Class 10 Ex 1.1
- Real Numbers Class 10 Ex 1.2
- Real Numbers Class 10 Ex 1.3
- Real Numbers Class 10 Ex 1.4
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 1 |
| Chapter Name | Real Numbers |
| Exercise | Ex 1.2 |
| Number of Questions Solved | 7 |
| Category | NCERT Solutions |
NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.2
Page No: 11
Question 1
Express each number as product of its prime factors:
(i) 140
(ii) 156
(iii) 3825
(iv) 5005
(v) 7429
Solution:
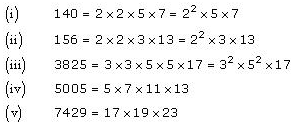
Concept Insight: Since the given number needs to be expressed as the product of prime factors so in order to solve this problem knowing prime numbers is required. Do not forget to put the exponent in case a prime number is repeating.
You can also Download Class 10 Maths NCERT Solutions to help you to revise complete Syllabus and score more marks in your examinations.
Question 2
Find the LCM and HCF of the following pairs of integers and verify that LCM × HCF = product of the two numbers.
(i) 26 and 91
(ii) 510 and 92
(iii) 336 and 54
Solution:
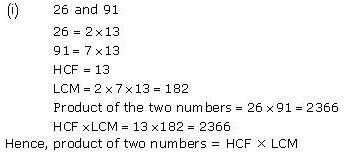

Concept Insight: HCF is the product of common prime factors raised to least power, while LCM is product of prime factors raised to the highest power. HCF is always a factor of the LCM.
Do not skip verification product of two numbers = HCF x LCM as it can help in cross checking the answer.
Question 3
Find the LCM and HCF of the following integers by applying the prime factorization method.
(i) 12, 15 and 21
(ii) 17, 23 and 29
(iii) 8, 9 and 25
Solution:

Concept Insight: HCF is the product of common prime factors of all three numbers raised to least power, while LCM is a product of prime factors of all here raised to the highest power. Use the fact that HCF is always a factor of the LCM to verify the answer. Note HCF of (a,b,c) can also be calculated by taking two numbers at a time i.e HCF (a,b) and then HCF (b,c) .
Question 4
Given that HCF (306, 657) = 9, find LCM (306, 657).
Solution:
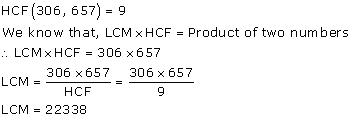
Concept Insight: This problem must be solved using a product of two numbers = HCF x LCM rather then prime factorization
Question 5
Check whether 6n can end with the digit 0 for any natural number n.
Solution:
If any number ends with the digit 0, it should be divisible by 10 or in other words its prime factorization must include primes 2 and 5 both Prime factorization of 6n = (2 x 3)n. By Fundamental Theorem of Arithmetic Prime factorization of a number is unique. So 5 is not a prime factor of 6n.
Hence, for any value of n, 6n will not be divisible by 5. Therefore, 6n cannot end with the digit 0 for any natural number n.
Concept Insight: In order to solve such problems the concept used is if a number is to end with zero then it must be divisible by 10 and the prime factorization of a number is unique.
Question 6
Explain why 7 × 11 × 13 + 13 and 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 are composite numbers.
Solution:
Numbers are of two types – prime and composite. Prime numbers have only two factors namely 1 and the number itself whereas composite numbers have factors other than 1 and itself.
It can be observed that
7 x 11 x 13 + 13 = 13 x (7 x 11 + 1) = 13 x (77 + 1)
= 13 x 78
= 13 x 13 x 6
The given expression has 6 and 13 as its factors. Therefore, it is a composite number.
7 x 6 x 5 x 4 x 3 x 2 x 1 + 5 = 5 x (7 x 6 x 4 x 3 x 2 x 1 + 1)
= 5 x (1008 + 1)
= 5 x 1009
1009 cannot be factorised further. Therefore, the given expression has 5 and 1009 as its factors. Hence, it is a composite number.
Concept Insight: Definition of prime numbers and composite numbers is used. Do not miss the reasoning.
Question 7
There is a circular path around a sports field. Sonia takes 18 minutes to drive one round of the field, while Ravi takes 12 minutes for the same. Suppose they both start at the same point and at the same time and go in the same direction. After how many minutes will they meet again at the starting point?
Solution:
It can be observed that Ravi and Sonia do not take the same amount of time Ravi takes lesser time than Sonia for completing 1 round of the circular path.
As they are going in the same direction, they will meet again at the same time when Ravi will have completed 1 round of that circular path with respect to Sonia.
i.e When Sonia completes one round then ravi completes 1.5 rounds. So they will meet first time at the time which is a common multiple of the time taken by them to complete 1 round
i.e LCM of 18 minutes and 12 minutes.
Now 18 = 2 x 3 x 3 = 2 x 32
And, 12 = 2 x 2 x 3 = 22 x 3
LCM of 12 and 18 = product of factors raised to highest exponent = 22 x 32 = 36
Therefore, Ravi and Sonia will meet together at the starting point after 36 minutes.
Concept Insight: In order to solve the word problems first step is to interpret the problem and identify what is to be determined. The problem asks for simultaneous reoccurrence of events so we need to find LCM. The key word for simultaneous reoccurrence of events is LCM. Do not forget to write the final answer.
We hope the NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.2 help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.2, drop a comment below and we will get back to you at the earliest.