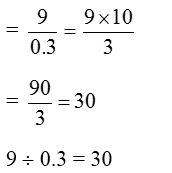How do you Multiply and Divide Decimals?
Multiplication of Decimal Numbers
Multiplication of a decimal by 10, 100, 1000 etc.:
Method:
On multiplying a decimal number by 10, 100, 1000, … the decimal point is shifted to the right by one, two, three, … places respectively.
For example,
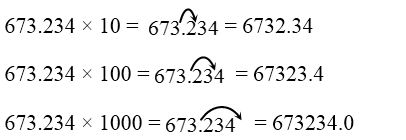
Multiplication of a decimal by a whole number:
Method :
Multiply the whole number by decimal (without the decimal point). Mark the decimal point in the product from right side to have as many decimals as there are in the given decimal.
For example, 12 × 3.82
First find the product of 12 and 382
(ignoring decimal) 382 × 12

Now, 3.82 × 12 = 45.84 (mark the point after two digits from right).
Multiplication of a decimal by a decimal:
Method :
1. Multiply the decimal numbers as of ordinary number (ignoring decimal points)
2. Mark the decimal point in the product after as many places (from the right) as the sum of the decimal places in the each number.
For example, 82.53 × 7.4
First find the product of 8253 and 74 (ignoring decimal point)
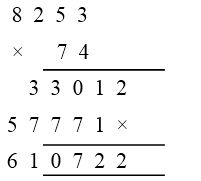
Now, 82.53 × 7.4 = 610.722 (mark the decimal point after (2 + 1 = 3) digits from right).
Multiplication of Decimal Numbers Problems with Solutions
1. Multiply : (i) 1.6 by 0.3 (ii) 8.03 by 2.9 (iii) 0.657 by 27
Solution:

2. Find the following products :
(i) 23.25 × 5 (ii) 2.325 × 25
Solution:
(i) 23.25 × 5
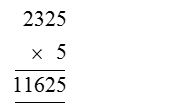
So, 23.25 × 5 = 116.25
Step 1 :
Multiply the multiplicand by the multiplier without bothering about the decimal point.
Step 2 :
Count the number of digits in the multiplicand after decimal point. It is 2 in this case. Count two digits from the unit place in the product and put a decimal point.
Therefore, 23.25 × 5 = 116.25
(ii) 2.325 × 25
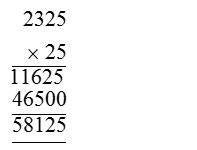
So, 2.325 × 25 = 58.125
Step 1 :
Multiply the multiplicand by the multiplier without bothering about the decimal point.
Step 2 :
The multiplicand has 3 places of decimal. Count three digits from the unit place of the product and put the decimal point.
Therefore, 2.325 × 25 = 58.125
3. Multiply 6.7 × 4.25 × 12.3
Solution:
(i) 6.7 × 4.25 × 12.3 = (6.7 × 4.25) × 12.3
= 28.475 × 12.3 = 350.2425

Also we can make the grouping as
(ii) 6.7 × 4.25 × 12.3
= 6.7 × (4.25 × 12.3) = 6.7 × 52.275
= 350.2425
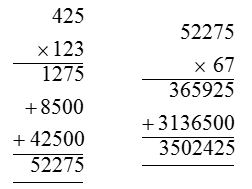
We find that
(6.7 × 4.25) × 12.3 = 6.7 × (4.25 × 12.3)
Hence,
To find the product of three decimal fractions, we can regroup them in any order, the result is the same in both cases. Thus, multiplication of decimals is associative.
4. Find (i) 10.05 × 1.05 (ii) 100.01 × 1.1
Solution:
(i) First multiply 1005 by 105
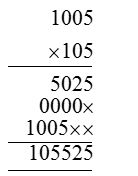
Sum of decimal places in the given decimal
= (2 + 2) = 4
So, product will contain 4 places of decimals from the right side.
10.05 × 1.05 = 10.5525
(ii) 100.01 × 1.1
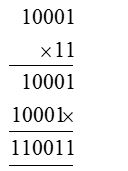
First multiply 10001 by 11.
Sum of decimal places in the given decimals
= (2 + 1) = 3
So, product will contain 3 places of decimals from the right side.
100.01 × 1.1 = 110.011
Division of Decimal Numbers
Dividing a decimal by 10, 100, 1000 etc.:
Method:
On dividing a number by 10, 100, 1000, … the digits of the number and quotient are same but the decimal point in the quotient shifts to left by one, two, three, … places.
For example,
3.27 ÷ 10 = 0.327
3.27 ÷ 100 = 0.0327
3.27 ÷ 1000 = 0.00327
Dividing a decimal by a whole number:
Method:
(i) Divide the dividend considering it as a whole number.
(ii) When the division of whole-number part of the dividend is complete, mark the decimal point in the quotient and proceed with the division as in case of whole number.
For example,

Dividing a decimal by a decimal:
Method:
(i) Convert the divisor into a whole number by multiplying it by 10, 100, 1000, … etc, depending upon the number of decimal places in it. Also we multiply the dividend by the same multiplier.
(ii) Divide the new dividend by the whole number obtained above.
For example, 22.08 ÷ 1.5
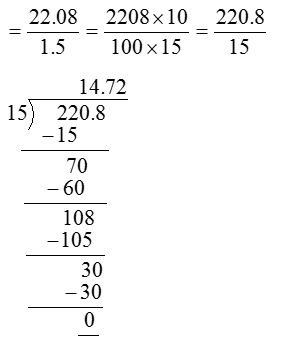
Read More About:
- What is the meaning of Place Value and Face Value in Maths?
- What is the Place Value Chart of an Indian and International System?
- What is a Decimal Value and Place Value of Decimals?
- How do you Round to the Nearest Ten Thousand
- What is the Definition of an Equivalent Decimal
- Converting To and From Scientific Notation
- What is the Difference between Ascending and Descending Order
- Addition and Subtraction of Decimals
- How do you Convert Fractions into Decimals and Vice Versa
- How do you Convert Unlike Decimals into Like Decimals
Division of Decimal Numbers Problems with Solutions
1. Find 15.225 ÷ 0.35
Solution:

Thus, we note that
15.225 ÷ 0.35 = 1522.5 ÷ 0.35 = 1522.5 ÷ 35
Thus if the decimal point is moved to two places towards right in the divisor then the decimal point is also moved to the right in dividend by same number of places.
2. Find 50.76 ÷ 9.4
Solution:
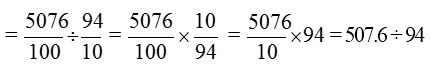
Hence, 50.76 ÷ 9.4 = 507.6 ÷ 94
Thus, we note that we can make the divisor as a whole number by shifting the decimal point to right by as many places as the number of the decimal places in the divisor. This way, the divisor is changed into a whole number.
3. Divide (i) 15.225 by 0.35 (ii) 50.76 ÷ 9.4
Solution:
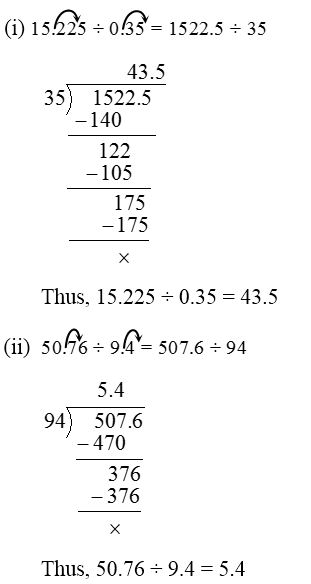
4. Find the quotient of 0.06688 ÷ 0.038
Solution:
Make the divisor a whole number by shifting the decimal point in dividend to the right by three places, 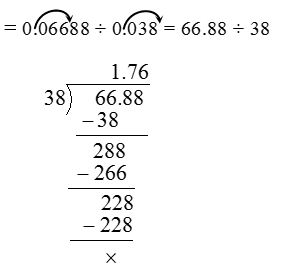
5. Find 0.024 ÷ 0.6
Solution:
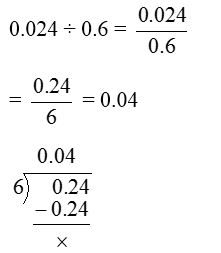
5. Find 64 ÷ 0.08
Solution:
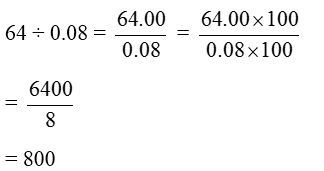
[Shift the decimal points two places to the right in both the numbers]
Dividing of a whole number by a decimal:
For example,