Problems on Simultaneous Linear Equations Class 9 ICSE ML Aggarwal

ML Aggarwal Class 9 Solutions Chapter 6 provides comprehensive guidance and step-by-step explanations for the concepts covered in this chapter Class 9 Mathematics. This chapter typically introduces fundamental mathematical concepts, laying the groundwork for future studies.

ML Aggarwal Class 9 Chapter 6 Solutions

ICSE Class 9 Maths Chapter 6 Solutions ML Aggarwal

Question 1.
The sum of two numbers is 50 and their difference is 16. Find the numbers.
Solution:

Question 2.
The sum of two numbers is 2. If their difference is 20, find the numbers.
Solution:

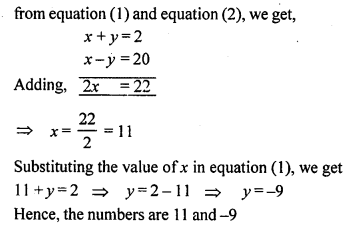
Question 3.
The sum of two numbers is 43. If the larger is doubled and the smaller is tripled, the difference is 36. Find the two numbers.
Solution:

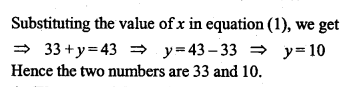
Question 4.
The cost of 5 kg of sugar and 7 kg of rice is Rs. 153, and the cost of 7 kg of sugar and 5 kg of rice is Rs. 147. Find the cost of 6 kg of sugar and 10 kg of rice.
Solution:

Question 5.
The class IX students of a certain public school wanted to give a farewell party to the outgoing students of class X. They decided to purchase two kinds of sweets, one costing Rs. 70 per kg and the other costing Rs. 84 per kg. They estimated that 36 kg of sweets were needed. If the total money spent on sweets was Rs. 2800, find how much sweets of each kind they purchased.
Solution:

Question 6.
If from twice the greater of two numbers 16 is subtracted, the result is half the other number. If from half the greater number 1 is subtracted, the result is still half the other number. What are the numbers.
Solution:

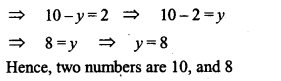
Question 7.
There are 38 coins in a collection of 20 paise coins and 25 paise coins. If the total value of the collection is Rs. 8.50, how many of each are there ?
Solution:

Question 8.
A man has certain notes of denominations Rs. 20 and Rs. 5 which amount to Rs. 380. If the number of notes of each kind is interchanged, they amount to Rs. 60 less as before. Find the number of notes of each denomination.
Solution:

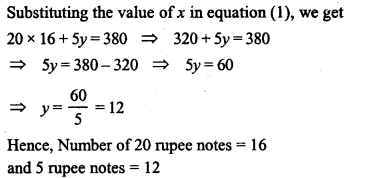
Question 9.
The ratio of two numbers is \(\frac { 2 }{ 3 }\). If 2 is subtracted from the first and 8 from the second, the ratio becomes the reciprocal of the original ratio. Find the numbers.
Solution:

Question 10.
If 1 is added to the numerator of a fraction, it becomes \(\frac { 1 }{ 5 }\) ; if 1 is taken from the denominator, it becomes \(\frac { 1 }{ 7 }\), find the fraction.
Solution:

Question 11.
If the numerator of a certain fraction is increased by 2 and the denominator by 1, the fraction becomes equal to \(\frac { 5 }{ 8 }\) and if the numerator and denominator are each diminished by 1, the fraction becomes equal to \(\frac { 1 }{ 2 }\) , find the fraction.
Solution:

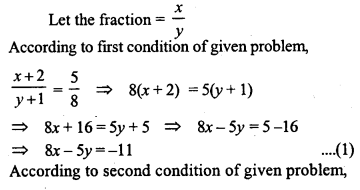
Question 12.
Find the fraction which becomes \(\frac { 1 }{ 2 }\) when the denominator is increased by 4 and is equal to \(\frac { 1 }{ 8 }\) , when the numerator is diminished by 5.
Solution:

Question 13.
In a two digit number the sum of the digits is 7. If the number with the order of the digits reversed is 28 greater than twice the unit’s digit of the original number, find the number.
Solution:

Question 14.
A number of two digits exceeds four times the sum of its digits by 6 and it is increased by 9 on reversing the digits. Find the number.
Solution:

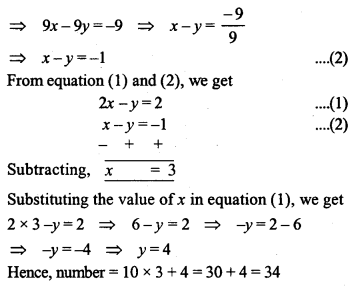
Question 15.
When a two digit number is divided by the sum of its digits the quotient is 8. If the ten’s digit is diminished by three times the unit’s digit the remainder is 1. What is the number ?
Solution:

Question 16.
The result of dividing a number of two digits by the number with digits reversed is 1 \(\frac { 3 }{ 4 }\) . If the sum of digits is 12, find the number.
Solution:

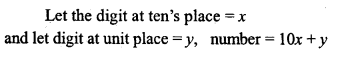
Question 17.
The result of dividing a number of two digits by the number with the digits reversed is \(\frac { 5 }{ 6 }\) . If the difference of digits is 1, find the number.
Solution:

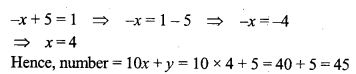
Question 18.
A number of three digits has the hundred digit 4 times the unit digit and the sum of three digits is 14. If the three digits are written in the reverse order, the value of the number is decreased by 594. Find the number.
Solution:

Question 19.
Four years ago Marina was three times old as her daughter. Six years from now the mother will be twice as old as her daughter. Find their present ages.
Solution:

Question 20.
On selling a tea set at 5% loss and a lemon set at 15% gain, a shopkeeper gains Rs. 70. If he sells the tea set at 5% gain and lemon set at 10% gain, he gains Rs. 130. Find the cost price of the lemon set.
Solution:

Question 21.
A person invested some money at 12% simple interest and some other amount at 10% simple interest. He received yearly interest of Rs, 1300. If he had interchanged the amounts, he would have received Rs. 40 more as yearly interest. How much did he invest at different rates ?
Solution:

Question 22.
A shopkeeper sells a table at 8% profit and a chair at 10% discount, thereby getting Rs. 1008. If he had sold the table at 10% profit and chair at 8% discount, he would have got Rs. 20 more. Find the cost price of the table and the list price of the chair.
Solution:

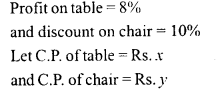
Question 23.
A and B have some money with them. A said to B, “if you give me Rs. 100, my money will become 75% of the money left with you.” B said to A” instead if you give me Rs. 100, your money will become 40% of my money, How much money did A and B have originally ?
Solution:

Question 24.
The students of a class are made to stand in (complete) rows. If one student is extra in a row, there would be 2 rows less, and if one student is less in a row, there would be 3 rows more. Find the number of students in the class.
Solution:

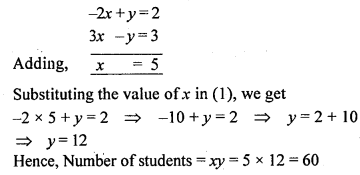
Question 25.
A jeweller has bars of 18-carat gold and 12- carat gold. How much of each must be melted together to obtain a bar of 16-carat gold weighing 120 grams ? (Pure gold is 24 carat)
Solution:

Question 26.
A and B together can do a piece of work in 15 days. If A’s one day work is 1 \(\frac { 1 }{ 2 }\) times the one day’s work of B, find in how many days can each do the work.
Solution:

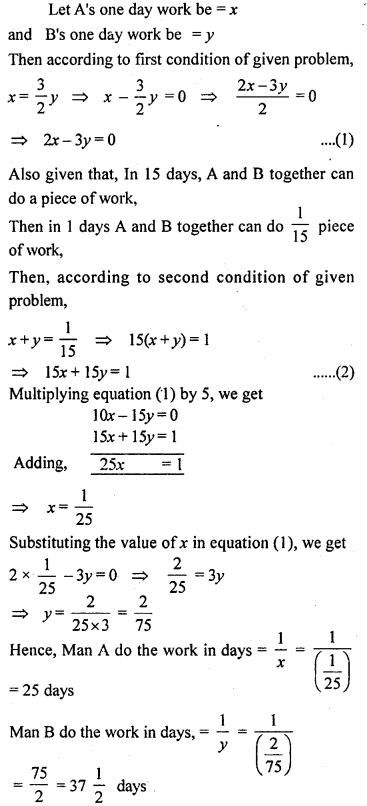
Question 27.
men and 5 women can do a piece of work in 4 days, while one man and one woman can finish it in 12 days. How long would it take for 1 man to do the work ?
Solution:

Question 28.
A train covered a certain distance at a uniform speed. If the train had been 30 km/hr faster, it would have taken 2 hours less than the scheduled time. If the train were slower by 15 km/hr, it would have taken 2 hours more than the scheduled time. Find the length of the journey.
Solution:

Question 29.
A boat takes 2 hours to go 40 km down the stream and it returns in 4 hours. Find the speed of the boat in still water and the speed of the stream.
Solution:

Question 30.
A boat sails a distance of 44 km in 4 hours with the current. It takes 4 hours 48 minutes longer to cover the same distance against the current. Find the speed of the boat in still water and the speed of the current.
Solution:

Question 31.
An aeroplane flies 1680 km with a head wind in 3.5 hours. On the return trip with same wind blowing, the plane takes 3 hours. Find the plane’s air speed and the wind speed.
Solution:

Question 32.
A part of monthly hostel charges is fixed and the remaining depends on the number of days one has taken food in the mess. When Bhawana takes food for 20 days, she has to pay Rs. 2600 as hostel charges; whereas when Divya takes food for 26 days, she pays Rs. 3020 as hostel charges. Find the fixed charges and the cost of food per day.
Solution:

Multiple Choice Questions

Choose the correct answer from the given four options (1 to 8):
Question 1.
Sum of digits of a two digit number is 8. If the number obtained by reversing the digits is 18 more than the original number, then the original number is
(a) 35
(b) 53
(c) 26
(d) 62
Solution:

Question 2.
The sum of two natural numbers is 25 and their difference is 7. The numbers are
(a) 17 and 8
(b) 16 and 9
(c) 18 and 7
(d) 15 and 10
Solution:

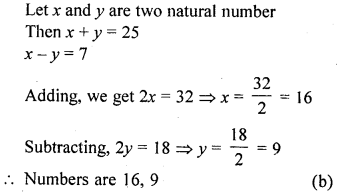
Question 3.
The sum of two natural numbers is 240 and their ratio is 3 : 5. Then the greater number is
(a) 180
(b) 160
(c) 150
(d) 90
Solution:

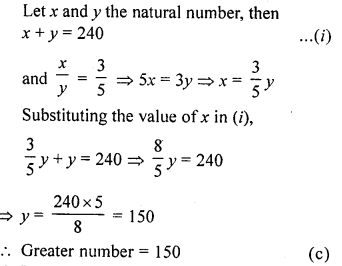
Question 4.
The sum of the digits of a two digit number is 9. If 27 is added to it, the digits of the number get reversed. The number
(a) 27
(b) 72
(c) 63
(d) 36
Solution:

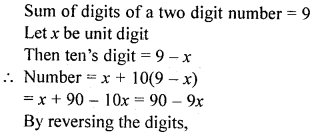
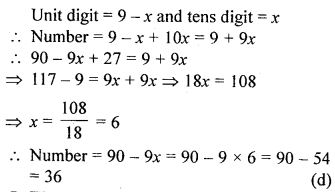
Question 5.
The sum of the digits of a two digit number is 12. If the number is decreased by 18, its digits get reversed. The number is
(a) 48
(b) 84
(c) 57
(d) 75
Solution:

Question 6.
Aruna has only ₹1 and ₹2 coins with her. If the total number of coins that she has is 50 and the amount of the money with her is ₹75, then the number of ₹1 and ₹2 coins are, respectively
(a) 35 and 15
(b) 35 and 20
(c) 15 and 75
(d) 25 and 25
Solution:

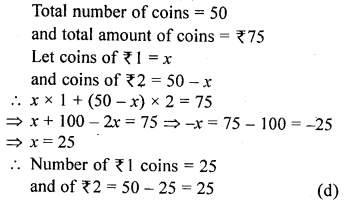
Question 7.
The age of a woman is four times the age of her daughter. Five years hence, the age of the woman will be three times the age of her daughter. The present age of the daughter is
(a) 40 years
(b) 20 years
(c) 15 years
(d) 10 years
Solution:

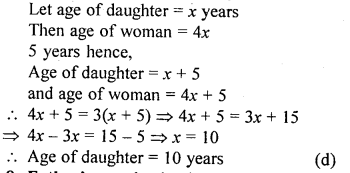
Question 8.
Father’s age is six times his son’s age. Four years hence, the age of the father will be four times his son’s age. The present age in years of the son and the father are, respectively
(a) 4 and 24
(b) 5 and 30
(c) 6 and 36
(d) 3 and 24
Solution:

Chapter Test

Question 1.
A 700 gm dry fruit packcosts Rs. 216. It contains some almonds and the rest cashew kernel. If almonds cost Rs. 288 ‘per kg and cashew kernel.cost Rs. 336 per kg, what are the quantities of the two dry fruits separately ?
Solution:

Question 2.
Drawing pencils cost 80 paise each and coloured pencils cost Rs. 1.10 each. If altogether two dozen pencils cost Rs. 21.60, how many coloured pencils are there ?
Solution:

Question 3.
Shikha works in a factory. In one week she earned Rs. 390 for working 47 hours, of which 7 hours were overtime. The next week she earned Rs. 416 for working 50 hours, of which 8 hours were overtime. What is Shikha’s hourly earning rate ?
Solution:

Question 4.
The sum of the digits of a two digit number is 7. If the digits are reversed, the new number increased by 3 equals 4 times the original number. Find the number.
Solution:

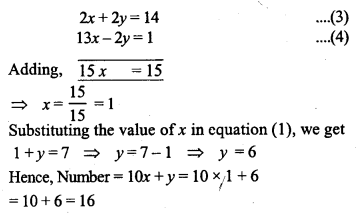
Question 5.
Three years hence a man’s age will be three times his son’s age and 7 years ago he was seven times as old as his son. How old are they now ?
Solution:

Question 6.
Rectangles are drawn on line segments of fixed lengths. When the breadths are 6 m and 5 m respectively the sum of the areas of the rectangles is 83 m². But if the breadths are 5 m and 4 m respectively the sum of the areas is 68 m². Find the sum of the areas of the squares drawn on the line segments.
Solution:

Question 7.
If the length and the breadth of a room are increased by 1 metre each, the area is increased by 21 square metres. If the length is decreased by 1 metre and the breadth is increased by 2 metres, the area is increased by 14 square metres. Find the perimeter of the room.
Solution:

Question 8.
The lenghts (in metres) of the sides of a triangle are 2x + \(\frac { y }{ 2 }\), \(\frac { 5x }{ 3 }\) + y + \(\frac { 1 }{ 2 }\) and \(\frac { 2 }{ 3 }\)x + 2y + \(\frac { 5 }{ 2 }\). If the triangle is equilateral, find its perimeter.
Solution:

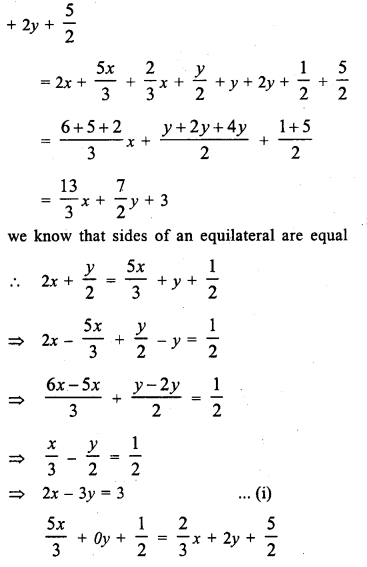
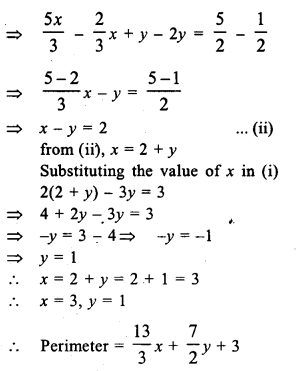
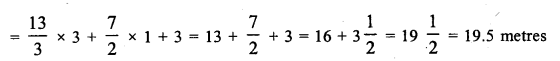
Question 9.
On Diwali eve, two candles, one of which is 3 cm longer than the other are lighted. The longer one is lighted at 530 p.m. and the shorter at 7 p.m. At 930 p.m. they both are of the same length. The longer one burns out at 1130 p.m. and the shorter one at 11 p.m. How long was each candle originally ?
Solution:

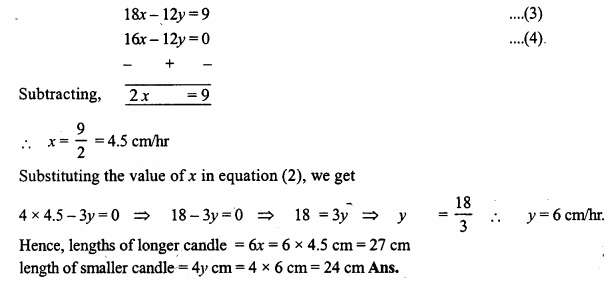
We hope that ML Aggarwal Class 9 Solutions for ICSE Maths Chapter 6 Problems on Simultaneous Linear Equations

are helpful  if you have doubts, comment below we will get back you as soon as possible