ML Aggarwal Class 9 Solutions Chapter 11 provides comprehensive guidance and step-by-step explanations for the concepts covered in this chapter Class 9 Mathematics. This chapter typically introduces fundamental mathematical concepts, laying the groundwork for future studies.
ML Aggarwal Class 9 Chapter 11 Solutions
ICSE Class 9 Maths Chapter 11 Solutions ML Aggarwal
Question 1.
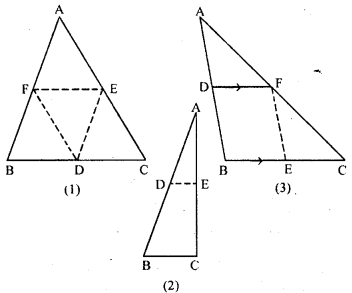
(a) In the figure (1) given below, D, E and F are mid-points of the sides BC, CA and AB respectively of ∆ ABC. If AB = 6 cm, BC = 4.8 cm and CA= 5.6 cm, find the perimeter of (i) the trapezium FBCE (ii) the triangle DEF.
(b) In the figure (2) given below, D and E are mid-points of the sides AB and AC respectively. If BC =
5.6 cm and∠B = 72°, compute (i) DE (ii)∠ADE.
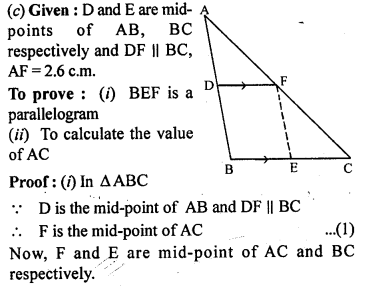
(c) In the figure (3) given below, D and E are mid-points of AB, BC respectively and DF || BC. Prove that DBEF is a parallelogram. Calculate AC if AF = 2.6 cm.
Solution:
(a) (i) Given : AB = 6 cm, BC = 4.8 cm, and CA = 5.6 cm
Required : The perimeter of trapezium FBCA.
Question 2.
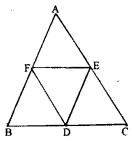
Prove that the four triangles formed by joining in pairs the mid-points of the sides c of a triangle are congruent to each other.
Solution:
Given: In ∆ ABC, D, E and r,
F are mid-points of AB, BC and CA respectively. Join DE, EF and FD.
Question 3.
If D, E and F are mid-points of sides AB, BC and CA respectively of an isosceles triangle ABC, prove that ∆DEF is also F, isosceles.
Solution:
Given : ABC is an isosceles triangle in which AB = AC
Question 4.
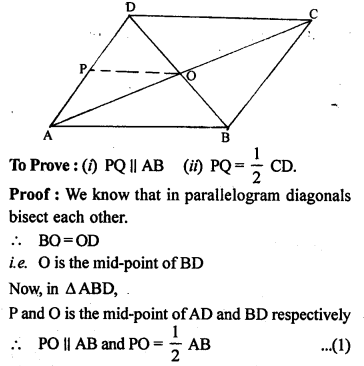
The diagonals AC and BD of a parallelogram ABCD intersect at O. If P is the mid-point of AD, prove that
(i) PQ || AB
(ii) PO=\(\frac { 1 }{ 2 }\)CD.
Solution:
(i) Given : ABCD is a parallelogram in which diagonals AC and BD intersect each other. At point O, P is the mid-point of AD. Join OP.
Question 5.
In the adjoining figure, ABCD is a quadrilateral in which P, Q, R and S are mid-points of AB, BC, CD and DA respectively. AC is its diagonal. Show that
(i) SR || AC and SR =\(\frac { 1 }{ 2 }\)AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.
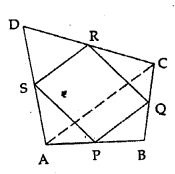
Solution:
Question 6.
Show that the quadrilateral formed by joining the mid-points of the adjacent sides of a square, is also a square,
Solution:
Question 7.
In the adjoining figure, AD and BE are medians of ∆ABC. If DF U BE, prove that CF = \(\frac { 1 }{ 4 }\) AC.
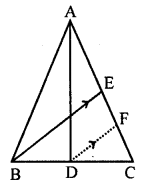
Solution:
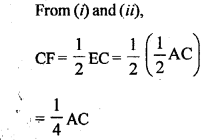
Question 8.
(a) In the figure (1) given below, ABCD is a parallelogram. E and F are mid-points of the sides AB and CO respectively. The straight lines AF and BF meet the straight lines ED and EC in points G and H respectively. Prove that
(i) ∆HEB = ∆HCF
(ii) GEHF is a parallelogram.
(b) In the diagram (2) given below, ABCD is a parallelogram. E is mid-point of CD and P is a point on AC such that PC = \(\frac { 1 }{ 4 }\) AC. EP produced meets BC at F. Prove that
(i) F is mid-point of BC (ii) 2EF = BD
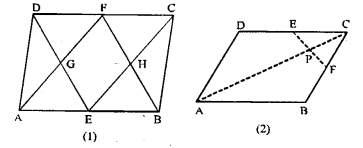
Solution:
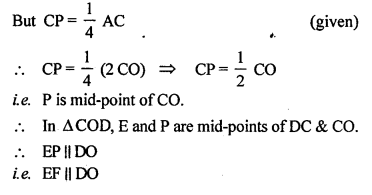
Question 9.
ABC is an isosceles triangle with AB = AC. D, E and F are mid-points of the sides BC, AB and AC respectively. Prove that the line segment AD is perpendicular to EF and is bisected by it.
Solution:
Question 10.
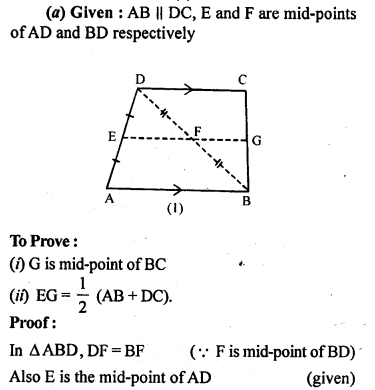
(a) In the quadrilateral (1) given below, AB || DC, E and F are mid-points of AD and BD respectively. Prove that:
Solution:
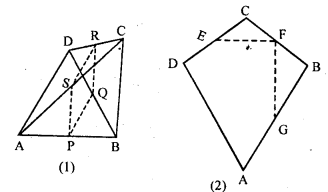
Question 11.
(a) In the quadrilateral (1) given below, AD = BC, P, Q, R and S are mid-points of AB, BD, CD and AC respectively. Prove that PQRS is a rhombus.
(b) In the figure (2) given below, ABCD is a kite in which BC = CD, AB = AD, E, F, G are mid-points of CD, BC and AB respectively. Prove that:
(i) ∠EFG = 90
(ii) The line drawn through G and parallel to FE bisects DA.
Solution:
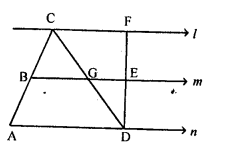
Question 12.
In the adjoining figure, the lines l, m and n are parallel to each other, and G is mid-point of CD. Calculate:
(i) BG if AD = 6 cm
(ii) CF if GE = 2.3 cm
(iii) AB if BC = 2.4 cm
(iv) ED if FD = 4.4 cm.
Solution:
Multiple Choice Questions
Choose the correct answer from the given four options (1 to 6):
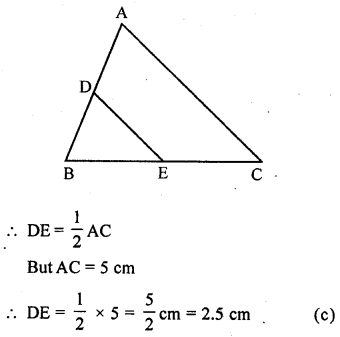
Question 1.
In a ∆ABC, AB = 3 cm, BC = 4 cm and CA = 5 cm. IfD and E are mid-points of AB and BC respectively, then the length of DE is
(a) 1.5 cm
(b) 2 cm
(c) 2.5 cm
(d) 3.5 cm
Solution:
In ∆ABC, D and E are the mid-points of sides AB and BC
Question 2.
In the given figure, ABCD is a rectangle in which AB = 6 cm and AD = 8 cm. If P and Q are mid-points of the sides BC and CD respectively, then the length of PQ is
(a) 7 cm
(b) 5 cm
(c) 4 cm
(d) 3 cm
Solution:
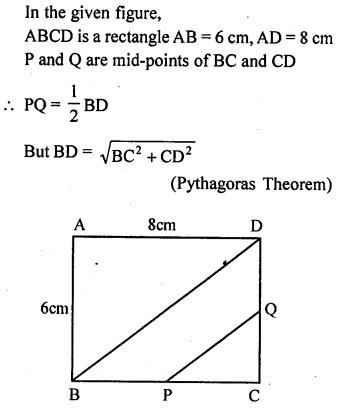
Question 3.
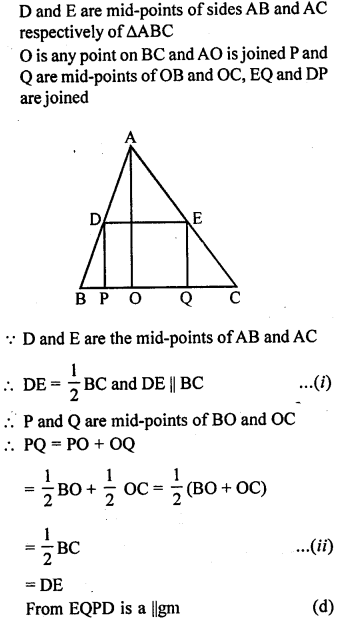
D and E are mid-points of the sides AB and AC of ∆ABC and O is any point on the side BC. O is joined to A. If P and Q are mid-points of OB and OC respectively, then DEQP is
(a) a square
(b) a rectangle
(c) a rhombus
(d) a parallelogram
Solution:
D and E are mid-points of sides AB and AC respectively of AABC O is any point on BC and AO is joined P and Q are mid-points of OB and OC, EQ and DP are joined
Question 4.
The quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rectanlge if
(a) PQRS is a parallelogram
(b) PQRS is a rectangle
(c) the diagonals of PQRS are perpendicular to each other
(d) the diagonals of PQRS are equal.
Solution:
A, B, C and D are the mid-points of the sides PQ, QR, RS and SP respectively
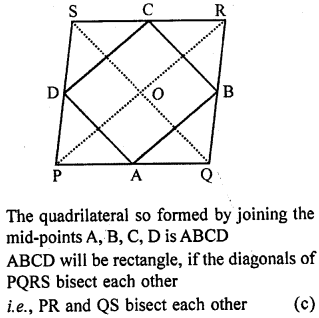
Question 5.
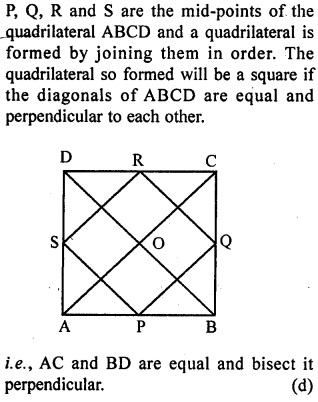
The quadrilateral formed by joining the mid-points of the sides of a quadrilateral ABCD, taken in order, is a rhombus if
(a) ABCD is a parallelogram
(b) ABCD is a rhombus
(c) the diagonals of ABCD are equal
(d) the diagonals of ABCD are perpendicular to each other.
Solution:
P, Q, R and S are the mid-points of the quadrilateral ABCD and a quadrilateral is formed by joining the mid-points in order
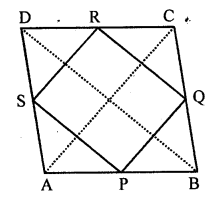
Question 6.
The figure formed by joining the mid points of the sides of a quadrilateral
ABCD, taken in order, is a square only if
(a) ABCD is a rhombus r
(b) diagonals of ABCD are equal
(c) diagonals of ABCD are perpendicular to each other
(d) diagonals of ABCD are equal and perpendicular to each other.
Solution:
Chapter Test
Question 1.
ABCD is a rhombus with P, Q and R as midpoints of AB, BC and CD respectively. Prove that PQ ⊥ QR.
Solution:
Question 2.
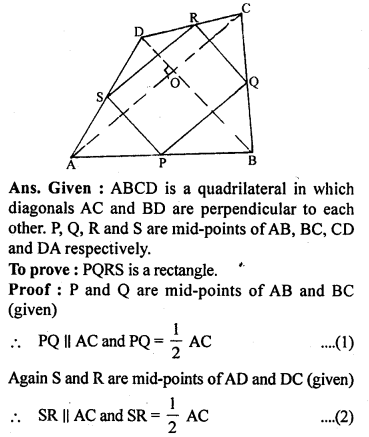
The diagonals of a quadrilateral ABCD are perpendicular. Show that the quadrilateral formed by joining the mid-points of its adjacent sides is a rectangle.
Solution:
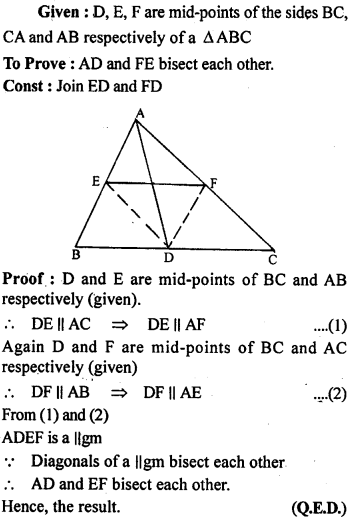
Question 3.
If D, E, F are mid-points of the sides BC, CA and AB respectively of a ∆ ABC, Prove that AD and FE bisect each other.
Solution:
Question 4.
In ∆ABC, D and E are mid-points of the sides AB and AC respectively. Through E, a straight line is drawn parallel to AB to meet BC at F. Prove that BDEF is a parallelogram. If AB = 8 cm and BC = 9 cm, find the perimeter of the parallelogram BDEF.
Solution:
In ∆ABC, D and E are the mid-points of
Question 5.
In the given figure, ABCD is a parallelogram and E is mid-point of AD. DL EB meets AB produced at F. Prove that B is mid-point of AF and EB = LF.
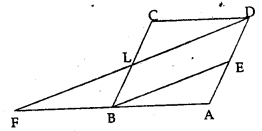
Solution:
Given In the figure
Question 6.
In the given figure, ABCD is a parallelogram. If P and Q are mid-points of sides CD and BC respectively. Show that CR = \(\frac { 1 }{ 2 }\) AC.
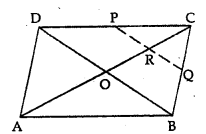
Solution:
