Triangles Class 9 ICSE ML Aggarwal

ML Aggarwal Class 9 Solutions Chapter 10 provides comprehensive guidance and step-by-step explanations for the concepts covered in this chapter Class 9 Mathematics. This chapter typically introduces fundamental mathematical concepts, laying the groundwork for future studies.

ML Aggarwal Class 9 Chapter 10 Solutions

ICSE Class 9 Maths Chapter 10 Solutions ML Aggarwal

Exercise 10.1

Question 1.
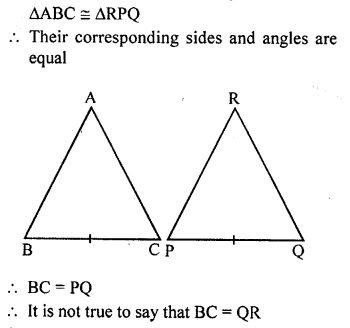
It is given that ∆ABC ≅ ∆RPQ. Is it true to say that BC = QR ? Why?
Solution:

Question 2.
“If two sides and an angle of one triangle are equal to two sides and an angle of another triangle, then the two triangles must be congruent.” Is the statement true? Why?
Solution:
No, it is not true statement as the angles should be included angle of there two given sides.

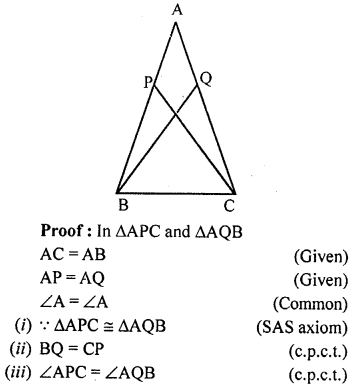
Question 3.
In the given figure, AB=AC and AP=AQ. Prove that
(i) ∆APC ≅ ∆AQB
(ii) CP = BQ
(iii) ∠APC = ∠AQB.
Solution:

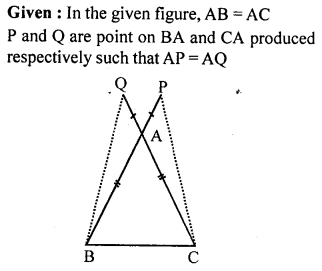
Question 4.
In the given figure, AB = AC, P and Q are points on BA and CA respectively such that AP = AQ. Prove that
(i) ∆APC ≅ ∆AQB
(ii) CP = BQ
(iii) ∠ACP = ∠ABQ.
Solution:

Question 5.
In the given figure, AD = BC and BD = AC. Prove that :
∠ADB = ∠BCA and ∠DAB = ∠CBA.

Solution:

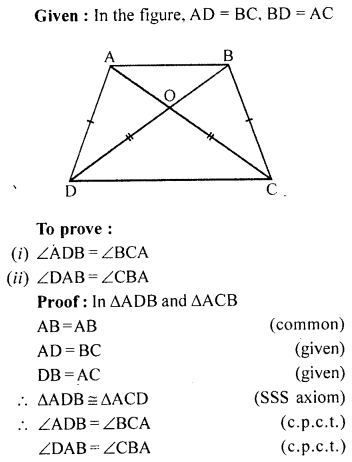
Question 6.
In the given figure, ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA. Prove that
(i) ∆ABD ≅ ∆BAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC.
Solution:

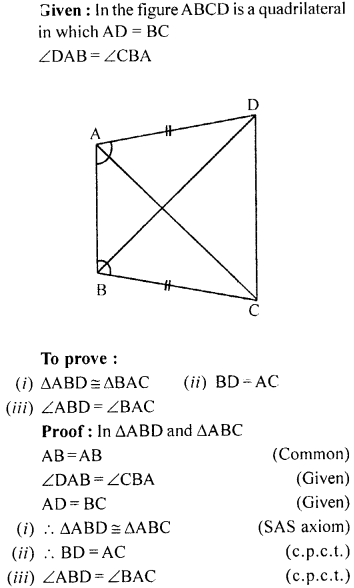
Question 7.
In the given figure, AB = DC and AB || DC. Prove that AD = BC.
Solution:

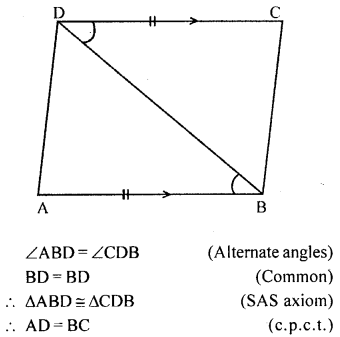
Question 8.
In the given figure. AC = AE, AB = AD and ∠BAD = ∠CAE. Show that BC = DE.

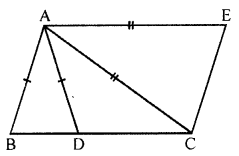
Solution:

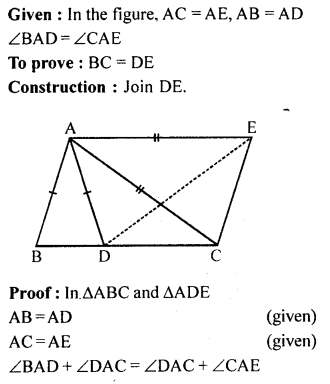
Question 9.
In the adjoining figure, AB = CD, CE = BF and ∠ACE = ∠DBF. Prove that
(i) ∆ACE ≅ ∆DBF
(ii) AE = DF.
Solution:

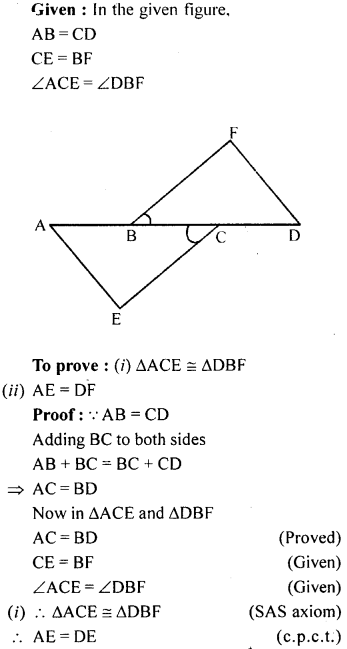
Question 10.
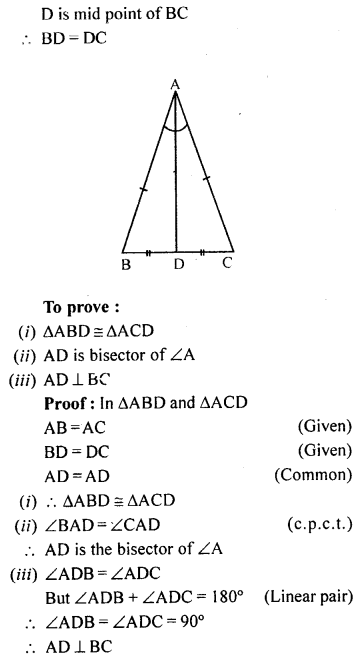
In the given figure, AB = AC and D is mid-point of BC. Use SSS rule of congruency to show that
(i) ∆ABD ≅ ∆ACD
(ii) AD is bisector of ∠A
(iii) AD is perpendicular to BC.
Solution:

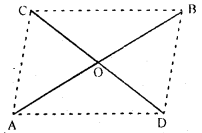
Question 11.
Two line segments AB and CD bisect each other at O. Prove that :
(i) AC = BD
(ii) ∠CAB = ∠ABD
(iii) AD || CB
(iv) AD = CB.

Solution:

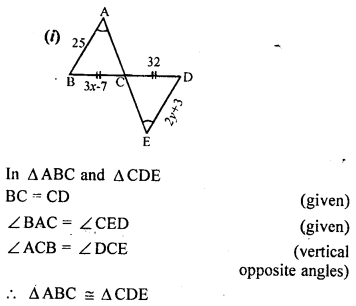
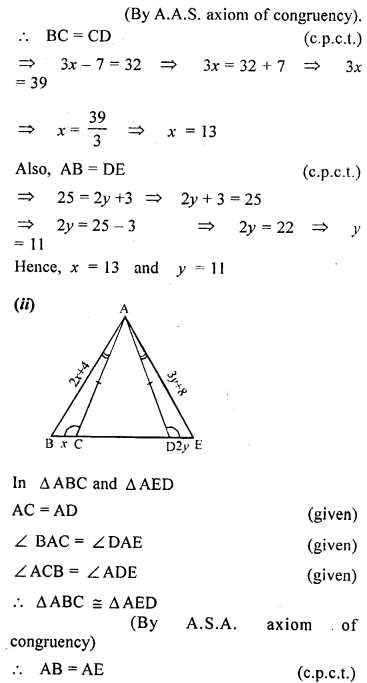
Question 12.
In each of the following diagrams, find the values of x and y.

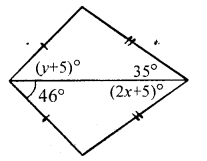
Solution:

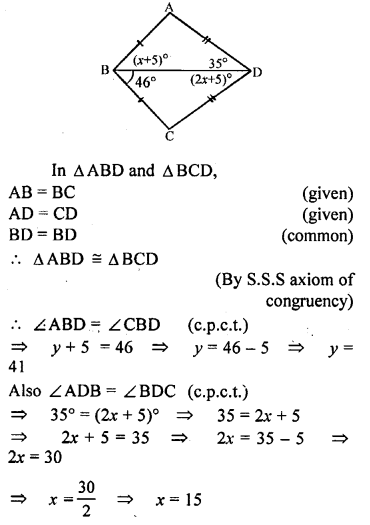
Exercise 10.2

Question 1.
In triangles ABC and PQR, ∠A= ∠Q and ∠B = ∠R. Which side of APQR should be equal to side AB of AABC so that the two triangles are congruent? Give reason for your answer.
Solution:

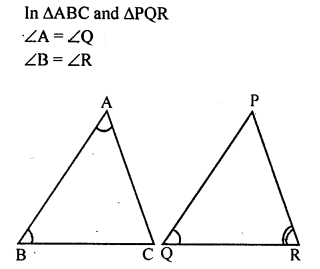
Question 2.
In triangles ABC and PQR, ∠A = ∠Q and ∠B = ∠R. Which side of APQR should be equal to side BC of AABC so that the two triangles are congruent? Give reason for your answer.
Solution:

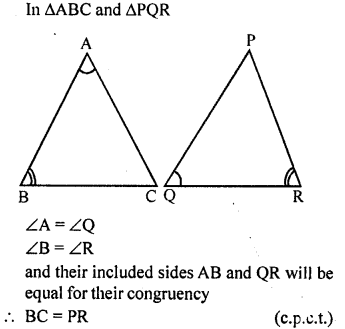
Question 3.
“If two angles and a side of one triangle are equal to two angles and a side of another triangle, then the two triangles must be congruent”. Is the statement true? Why?
Solution:
The given statement can be true only if the corresponding (included) sides are equal otherwise not.

Question 4.
In the given figure, AD is median of ∆ABC, BM and CN are perpendiculars drawn from B and C respectively on AD and AD produced. Prove that BM = CN.
Solution:

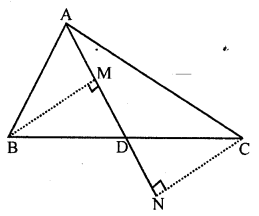
Question 5.
In the given figure, BM and DN are perpendiculars to the line segment AC. If BM = DN, prove that AC bisects BD.

Solution:

Question 6.
In the given figure, l and m are two parallel lines intersected by another pair of parallel lines p and q. Show that ∆ABC ≅ ∆CDA.

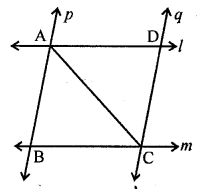
Solution:

Question 7.
In the given figure, two lines AB and CD intersect each other at the point O such that BC || DA and BC = DA. Show that O is the mid-point of both the line segments AB and CD.
Solution:

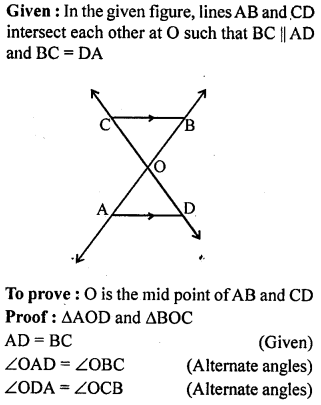
Question 8.
In the given figure, ∠BCD = ∠ADC and ∠BCA = ∠ADB. Show that
(i) ∆ACD ≅ ∆BDC
(ii) BC = AD
(iii) ∠A = ∠B.
Solution:

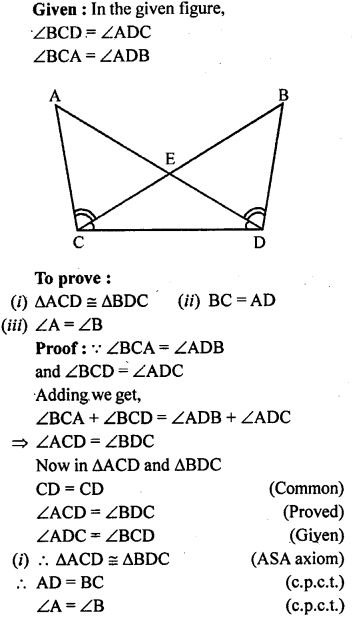
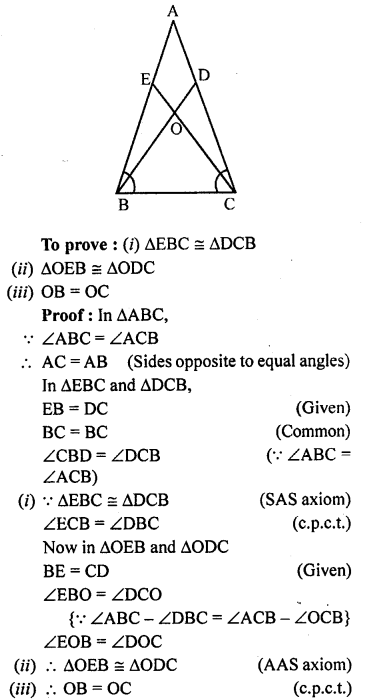
Question 9.
In the given figure, ∠ABC = ∠ACB, D and E are points on the sides AC and AB respectively such that BE = CD. Prove that
(i) ∆EBC ≅ ∆DCB
(ii) ∆OEB ≅ ∆ODC
(iii) OB = OC.
Solution:

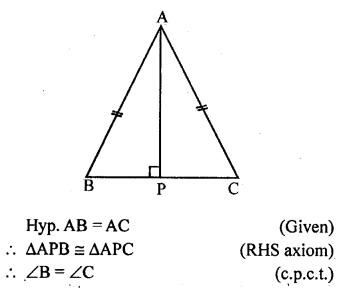
Question 10.
ABC is an isosceles triangle with AB=AC. Draw AP ⊥ BC to show that ∠B = ∠C.
Solution:

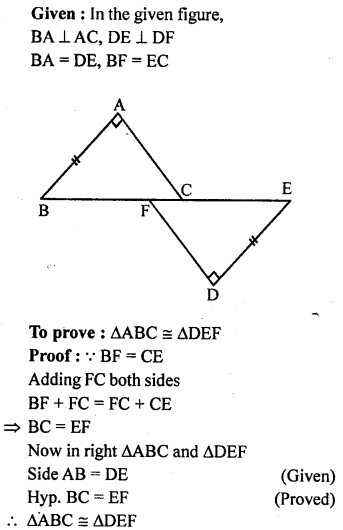
Question 11.
In the given figure, BA ⊥ AC, DE⊥ DF such that BA = DE and BF = EC.
Solution:

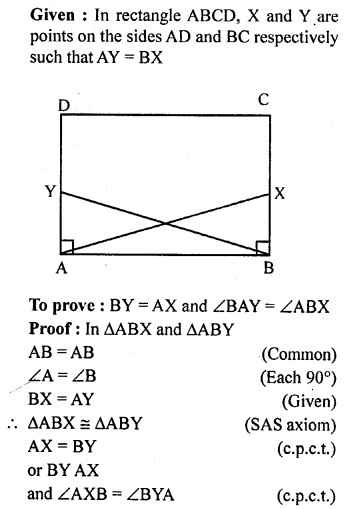
Question 12.
ABCD is a rectanige. X and Y are points on sides AD and BC respectively such that AY = BX. Prove that BY = AX and ∠BAY = ∠ABX.
Solution:

Question 13.
(a) In the figure (1) given below, QX, RX are bisectors of angles PQR and PRQ respectively of A PQR. If XS⊥ QR and XT ⊥ PQ, prove that
(i) ∆XTQ ≅ ∆XSQ
(ii) PX bisects the angle P.
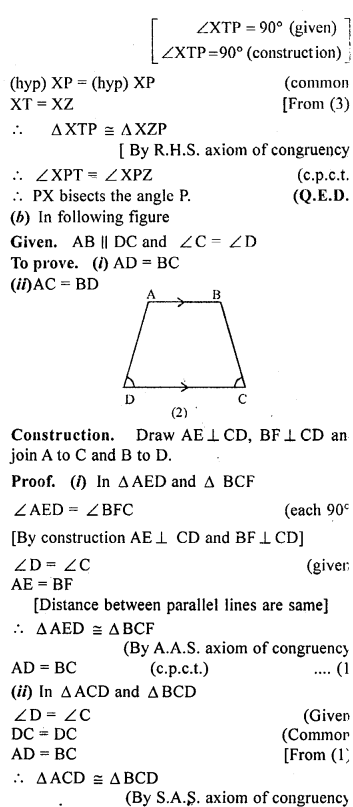
(b) In the figure (2) given below, AB || DC and ∠C = ∠D. Prove that
(i) AD = BC
(ii) AC = BD.
(c) In the figure (3) given below, BA || DF and CA II EG and BD = EC . Prove that, .
(i) BG = DF
(ii) EG = CF.


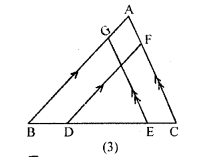
Solution:

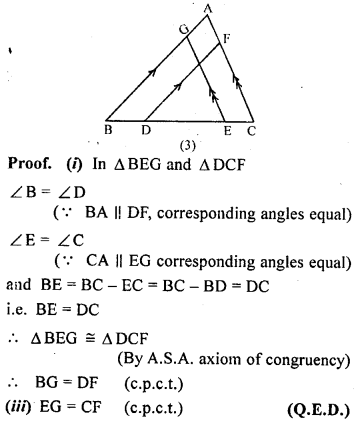
Question 14.
In each of the following diagrams, find the values of x and y.

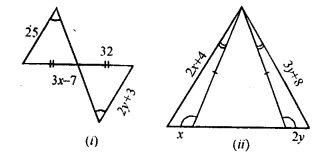
Solution:

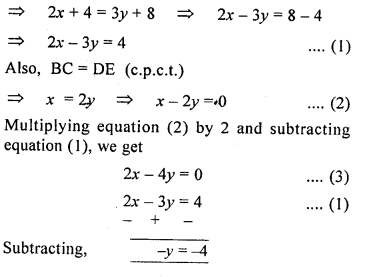
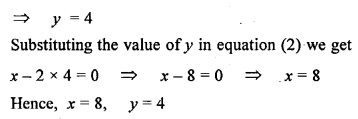
Exercise 10.3

Question 1.
ABC is a right angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.
Solution:

Question 2.
Show that the angles of an equilateral triangle are 60° each.
Solution:

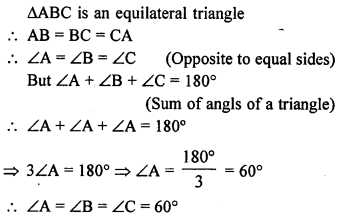
Question 3.
Show that every equiangular triangle is equilateral.
Solution:

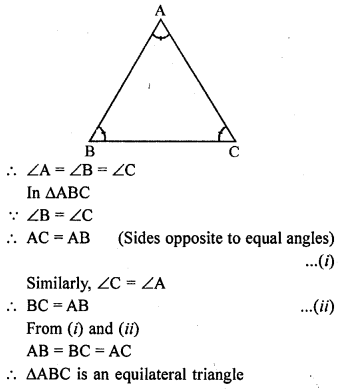
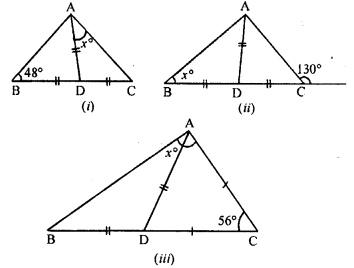
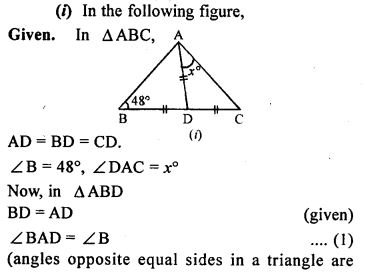
Question 4.
In the following diagrams, find the value of x:

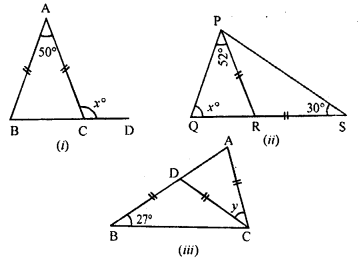
Solution:

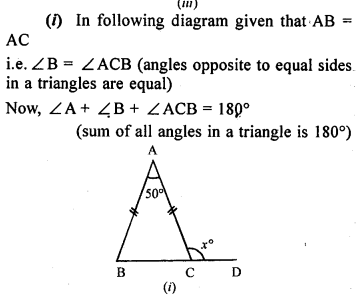
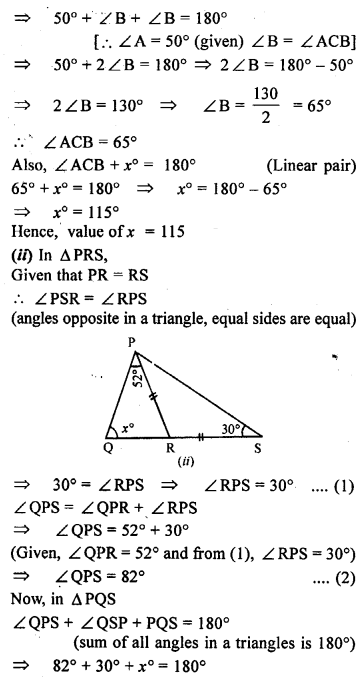
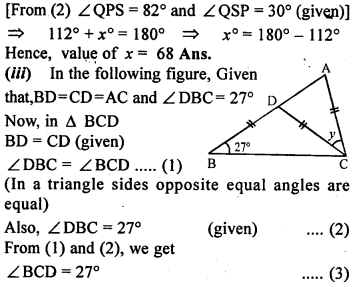
Question 5.
In the following diagrams, find the value of x:

Solution:

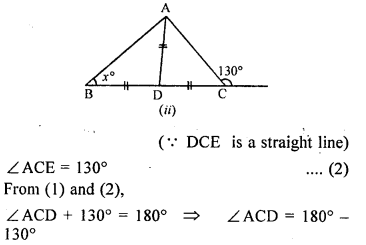
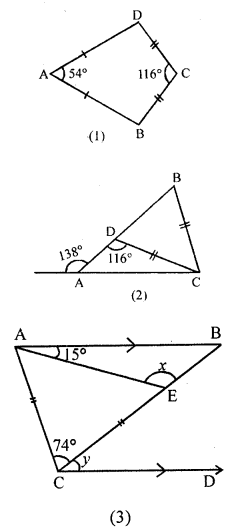
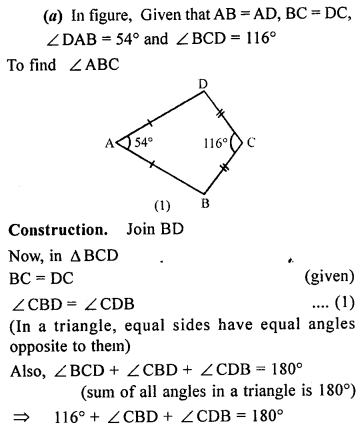
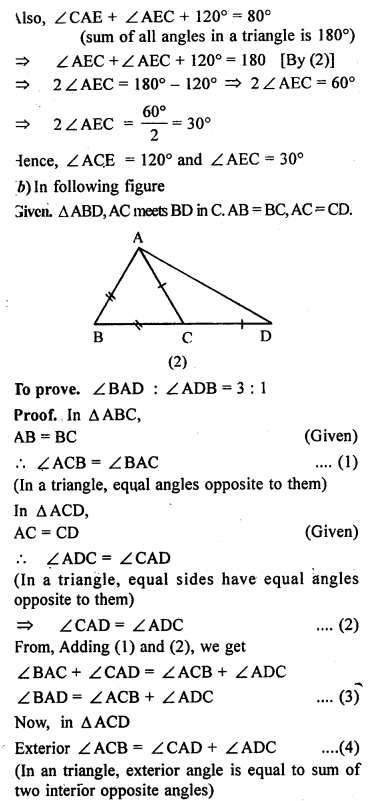
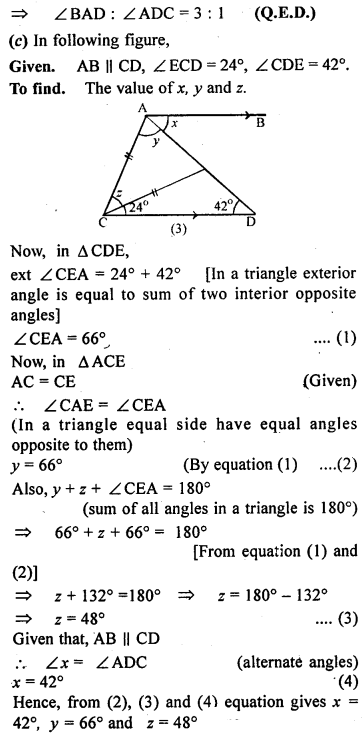
Question 6.
(a) In the figure (1) given below, AB = AD, BC = DC. Find ∠ ABC.
(b)In the figure (2) given below, BC = CD. Find ∠ACB.
(c) In the figure (3) given below, AB || CD and CA = CE. If ∠ACE = 74° and ∠BAE =15°, find the values of x and y.
Solution:

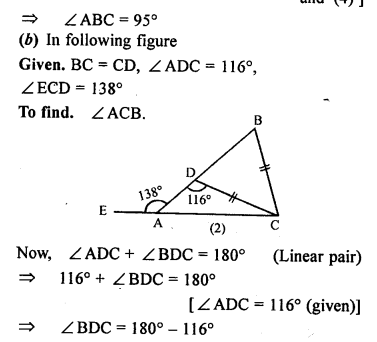
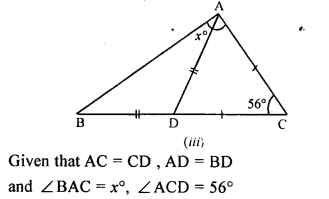
Question 7.
In ∆ABC, AB = AC, ∠A = (5x + 20)° and each of the base angle is \(\frac { 2 }{ 5 }\) th of ∠A. Find the measure of ∠A.
Solution:

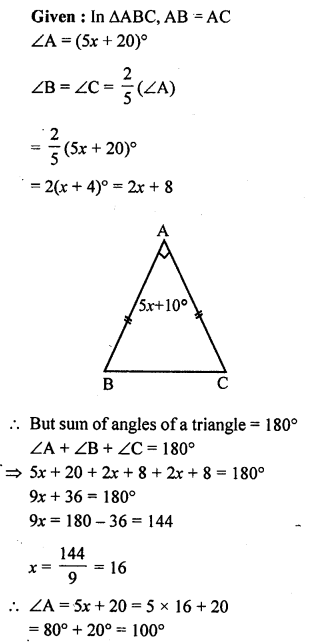
Question 8.
(a) In the figure (1) given below, ABC is an equilateral triangle. Base BC is produced to E, such that BC’= CE. Calculate ∠ACE and ∠AEC.
(b) In the figure (2) given below, prove that ∠ BAD : ∠ ADB = 3 : 1.
(c) In the figure (3) given below, AB || CD. Find the values of x, y and ∠.

Solution:

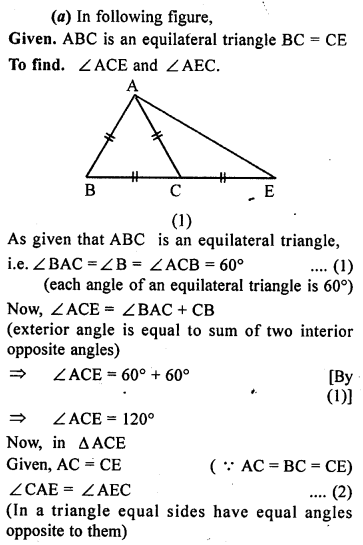
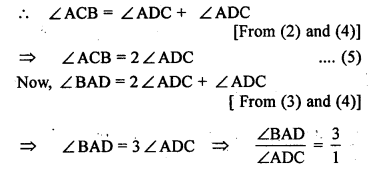
Question 9.
In the given figure, D is mid-point of BC, DE and DF are perpendiculars to AB and AC respectively such that DE = DF. Prove that ABC is an isosceles triangle.

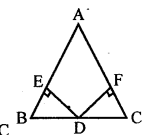
Solution:

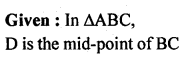
Question 10.
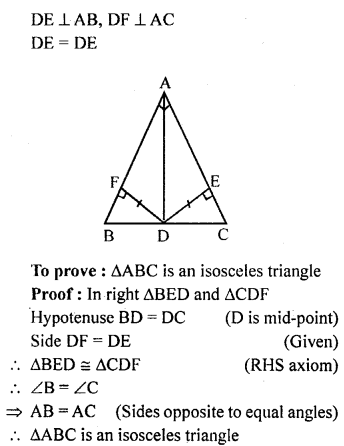
In the given figure, AD, BE and CF arc altitudes of ∆ABC. If AD = BE = CF, prove that ABC is an equilateral triangle.
Solution:

Question 11.
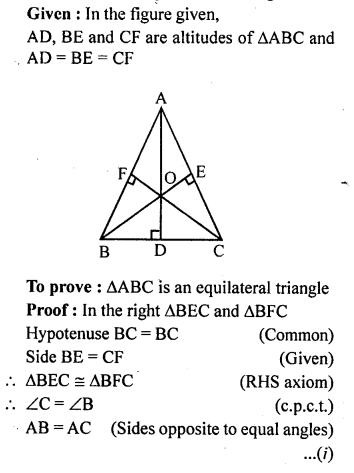
In a triangle ABC, AB = AC, D and E are points on the sides AB and AC respectively such that BD = CE. Show that:
(i) ∆DBC ≅ ∆ECB
(ii) ∠DCB = ∠EBC
(iii) OB = OC,where O is the point of intersection of BE and CD.
Solution:

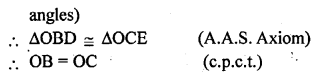
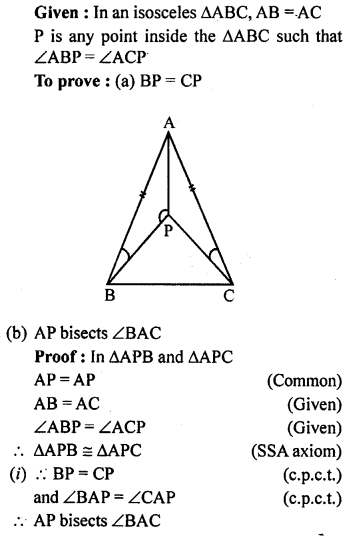
Question 12.
ABC is an isosceles triangle in which AB = AC. P is any point in the interior of ∆ABC such that ∠ABP = ∠ACP. Prove that
(a) BP = CP
(b) AP bisects ∠BAC.
Solution:

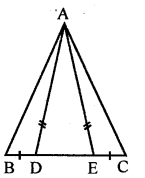
Question 13.
In the adjoining figure, D and E are points on the side BC of ∆ABC such that BD = EC and AD = AE. Show that ∆ABD ≅ ∆ACE.
Solution:

Question 14.
(a) In the figure (i) given below, CDE is an equilateral triangle formed on a side CD of a square ABCD. Show that ∆ADE ≅ ∆BCE and hence, AEB is an isosceles triangle.

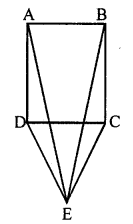
(b) In the figure (ii) given below, O is a point in the interior of a square ABCD such that OAB is an equilateral trianlge. Show that OCD is an isosceles triangle.

Question 15.
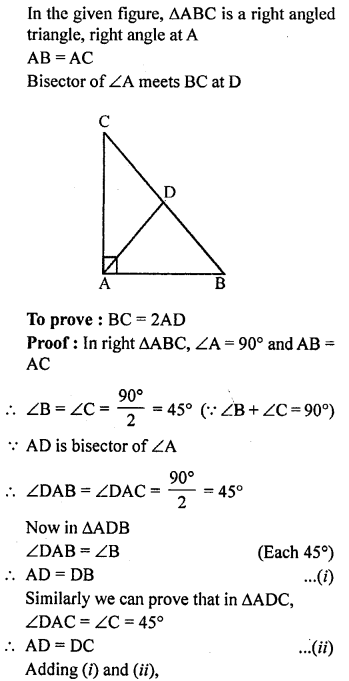
In the given figure, ABC is a right triangle with AB = AC. Bisector of ∠A meets BC at D. Prove that BC = 2AD.
Solution:

Exercise 10.4

Question 1.
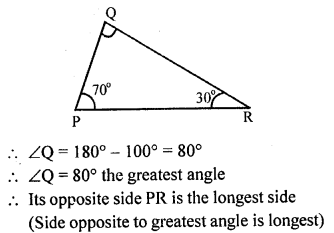
In ∆PQR, ∠P = 70° and ∠R = 30°. Which side of this triangle is longest? Give reason for your answer.
Solution:

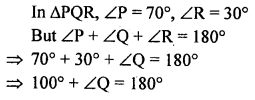
Question 2.
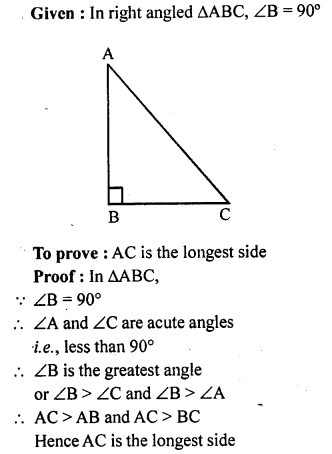
Show that in a right angled triangle, the hypotenuse is the longest side.
Solution:

Question 3.
PQR is a right angle triangle at Q and PQ : QR = 3:2. Which is the least angle.
Solution:

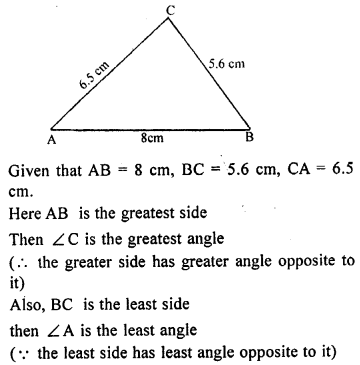
Question 4.
In ∆ ABC, AB = 8 cm, BC = 5.6 cm and CA = 6.5 cm. Which is (i) the greatest angle ?
(ii) the smallest angle ?
Solution:

Question 5.
In ∆ABC, ∠A = 50°, ∠B= 60°, Arrange the sides of the triangle in ascending order.
Solution:

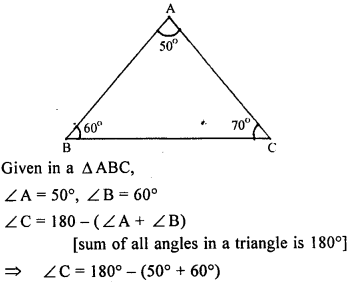
Question 6.
In figure given alongside, ∠B = 30°, ∠C = 40° and the bisector of ∠A meets BC at D. Show
(i) BD > AD
(ii) DC > AD
(iii) AC > DC
(iv) AB > BD

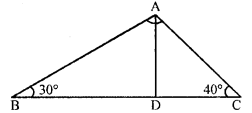
Solution:

Question 7.
(a) In the figure (1) given below, AD bisects ∠A. Arrange AB, BD and DC in the descending order of their lengths.
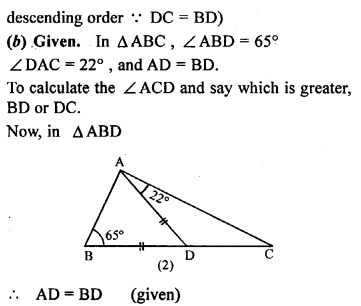
(b) In the figure (2) given below, ∠ ABD = 65°, ∠DAC = 22° and AD = BD. Calculate ∠ ACD and state (giving reasons) which is greater : BD or DC ?

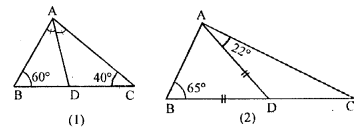
Solution:

Question 8.
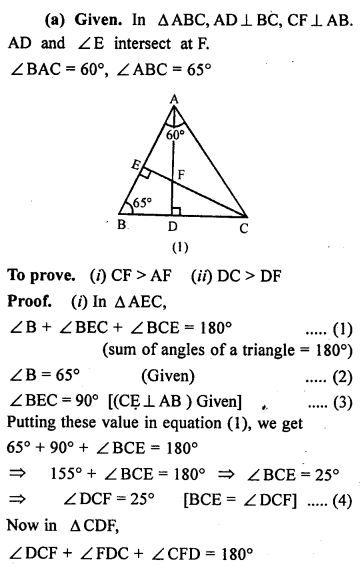
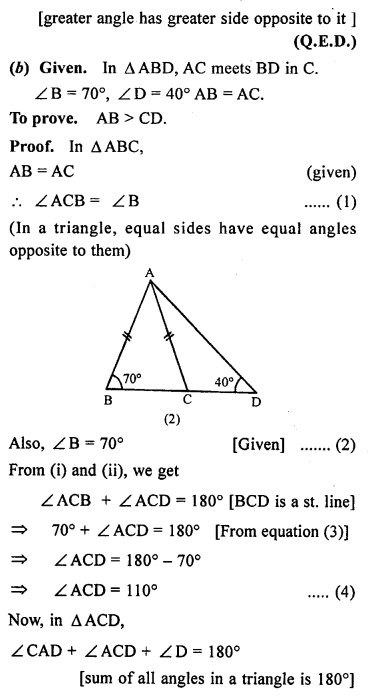
(a) In the figure (1) given below, prove that (i) CF> AF (ii) DC>DF.
(b) In the figure (2) given below, AB = AC.
Prove that AB > CD.
(c) In the figure (3) given below, AC = CD. Prove that BC < CD.

Solution:

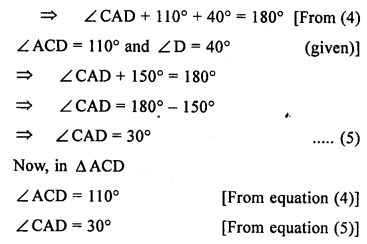
Question 9.
(a) In the figure (i) given below, ∠B < ∠A and ∠C < ∠D. Show that AD < BC. (b) In the figure (ii) given below, D is any point on the side BC of ∆ABC. If AB > AC, show that AB > AD.
Solution:

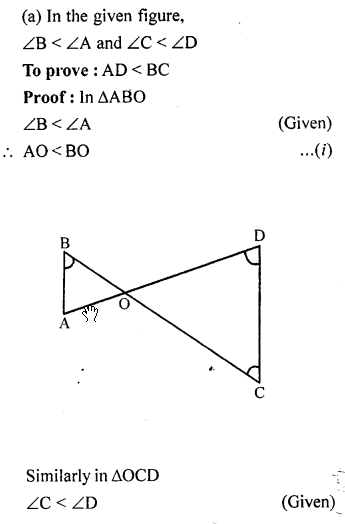
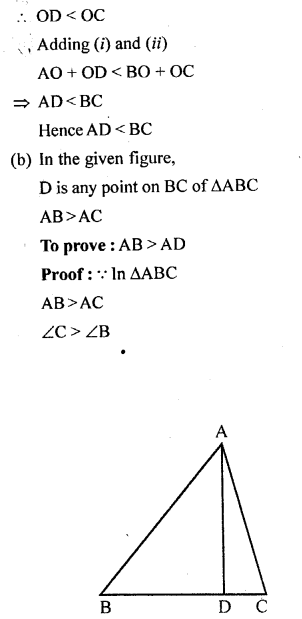
Question 10.
(i) Is it possible to construct a triangle with lengths of its sides as 4 cm, 3 cm and 7 cm? Give reason for your answer,
(ii) Is it possible to construct a triangle with lengths of its sides as 9 cm, 7 cm and 17 cm? Give reason for your answer.
(iii) Is it possible to construct a triangle with lengths of its sides as 8 cm, 7 cm and 4 cm? Give reason for your answer.
Solution:
(i) Length of sides of a triangle are 4 cm, 3 cm and 7 cm
We know that sum of any two sides of a triangle is greatar than its third side But 4 + 3 = 7 cm
Which is not possible
Hence to construction of a triangle with sides 4 cm, 3 cm and 7 cm is not possible.
(ii) Length of sides of a triangle are 9 cm, 7 cm and 17 cm
We know that sum of any two sides of a triangle is greater than its third side Now 9 + 7 = 16 < 17 ∴ It is not possible to construct a triangle with these sides.
(iii) Length of sides of a triangle are 8 cm, 7 cm and 4 cm We know that sum of any two sides of a triangle is greater than its third side Now 7 + 4 = 11 > 8
Yes, It is possible to construct a triangle with these sides.

Multiple Choice Questions

Choose the correct answer from the given four options (1 to 18):
Question 1.
Which of the following is not a criterion for congruency of triangles?
(a) SAS
(b) ASA
(c) SSA
(d) SSS
Solution:
Criteria of congruency of two triangles ‘SSA’ is not the criterion. (c)

Question 2.
In the adjoining figure, AB = FC, EF=BD and ∠AFE = ∠CBD. Then the rule by which ∆AFE = ∆CBD is
(a) SAS
(b) ASA
(c) SSS
(d) AAS

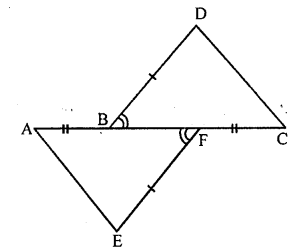
Solution:

Question 3.
In the adjoining figure, AB ⊥ BE and FE ⊥ BE. If AB = FE and BC = DE, then
(a) ∆ABD ≅ ∆EFC
(b) ∆ABD ≅ ∆FEC
(c) ∆ABD ≅ ∆ECF
(d) ∆ABD ≅ ∆CEF
Solution:
In the figure given,

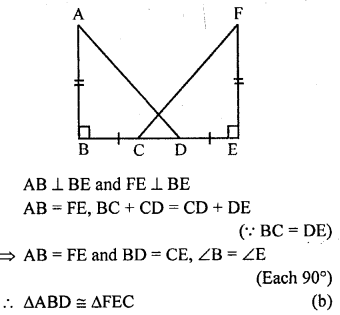
Question 4.
In the adjoining figure, AB=AC and AD is median of ∆ABC, then AADC is equal to
(a) 60°
(b) 120°
(c) 90°
(d) 75°
Solution:

Question 5.
In the adjoining figure, O is mid point of AB. If ∠ACO = ∠BDO, then ∠OAC is equal to
(a) ∠OCA
(b) ∠ODB
(c) ∠OBD
(d) ∠BOD
Solution:

Question 6.
In the adjoining figure, AC = BD. If ∠CAB = ∠DBA, then ∠ACB is equal to
(a) ∠BAD
(b) ∠ABC
(c) ∠ABD
(d) ∠BDA

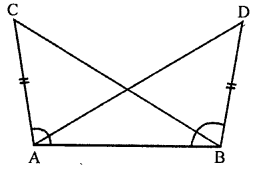
Solution:

Question 7.
In the adjoining figure, ABCD is a quadrilateral in which BN and DM are drawn perpendiculars to AC such that BN = DM. If OB = 4 cm, then BD is
(a) 6 cm
(b) 8 cm
(c) 10 cm
(d) 12 cm
Solution:

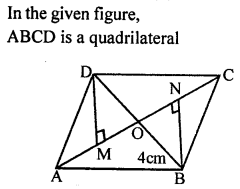
Question 8.
In ∆ABC, AB = AC and ∠B = 50°. Then ∠C is equal to
(a) 40°
(b) 50°
(c) 80°
(d) 130°
Solution:

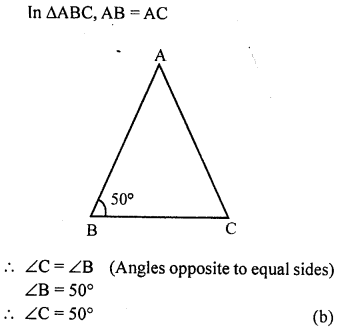
Question 9.
In ∆ABC, BC = AB and ∠B = 80°. Then ∠A is equal to
(a) 80°
(b) 40°
(c) 50°
(d) 100°
Solution:

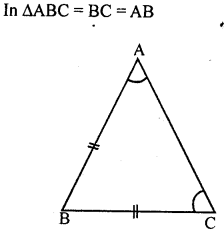
Question 10.
In ∆PQR, ∠R = ∠P, QR = 4 cm and PR = 5 cm. Then the length of PQ is
(a) 4 cm
(b) 5 cm
(c) 2 cm
(d) 2.5 cm
Solution:

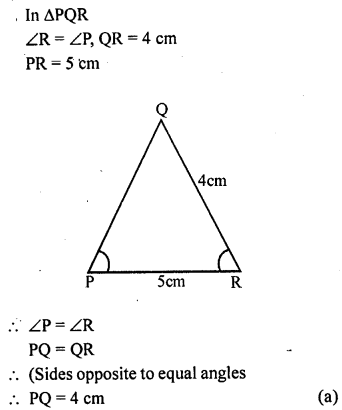
Question 11.
In ∆ABC and APQR, AB = AC, ∠C = ∠P and ∠B = ∠Q. The two triangles are
(a) isosceles but not congruent
(b) isosceles and congruent
(c) congruent but isosceles
(d) neither congruent nor isosceles
Solution:

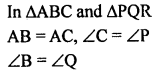
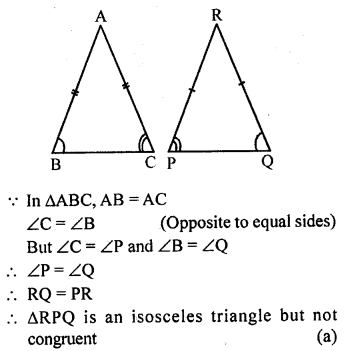
Question 12.
Two sides of a triangle are of lenghts 5 cm and 1.5 cm. The length of the third side of the triangle can not be
(a) 3.6 cm
(b) 4.1 cm
(c) 3.8 cm
(d) 3.4 cm
Solution:

Question 13.
If a, b, c are the lengths of the sides of a trianlge, then
(a) a – b > c
(b) c > a + b
(c) c = a + b
(d) c < A + B
Solution:
a, b, c are the lengths of the sides of a trianlge than a + b> c or c < a + b
(Sum of any two sides is greater than its third side) (d)

Question 14.
It is not possible to construct a triangle when the lengths of its sides are
(a) 6 cm, 7 cm, 8 cm
(b) 4 cm, 6 cm, 6 cm
(c) 5.3 cm, 2.2 cm, 3.1 cm
(d) 9.3 cm, 5.2 cm, 7.4 cm
Solution:
We know that sum of any two sides of a triangle is greater than its third side 2.2 + 3.1 = 5.3 ⇒ 5.3 = 5.3 is not possible (c)

Question 15.
In ∆PQR, if ∠R> ∠Q, then
(a) QR > PR
(b) PQ > PR
(c) PQ < PR
(d) QR < PR
Solution:
In ∆PQR, ∠R> ∠Q
∴ PQ > PR (b)

Question 16.
If triangle PQR is right angled at Q, then
(a) PR = PQ
(b) PR < PQ
(c) PR < QR
(d) PR > PQ
Solution:

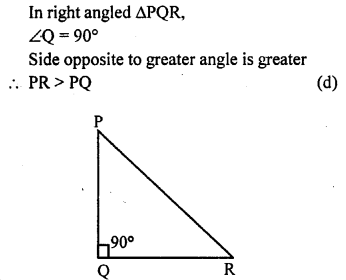
Question 17.
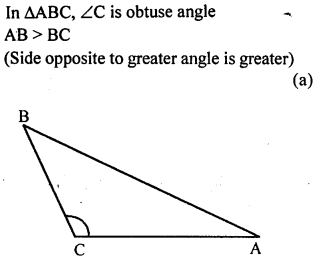
If triangle ABC is obtuse angled and ∠C is obtuse, then
(a) AB > BC
(b) AB = BC
(c) AB < BC
(d) AC > AB
Solution:

Question P.Q.
A triangle can be constructed when the lengths of its three sides are
(a) 7 cm, 3 cm, 4 cm
(b) 3.6 cm, 11.5 cm, 6.9 cm
(c) 5.2 cm, 7.6 cm, 4.7 cm
(d) 33 mm, 8.5 cm, 49 mm
Solution:
We know that in a triangle, if sum of any two sides is greater than its third side, it is possible to construct it 5.2 cm, 7.6 cm, 4.7 cm is only possible. (c)

Question P.Q.
A unique triangle cannot be constructed if its
(a) three angles are given
(b) two angles and one side is given
(c) three sides are given
(d) two sides and the included angle is given
Solution:
A unique triangle cannot be constructed if its three angle are given, (a)

Question 18.
If the lengths of two sides of an isosceles are 4 cm and 10 cm, then the length of the third side is
(a) 4 cm
(b) 10 cm
(c) 7 cm
(d) 14 cm
Solution:
Lengths of two sides of an isosceles triangle are 4 cm and 10 cm, then length of the third side is 10 cm
(Sum of any two sides of a triangle is greater than its third side and 4 cm is not possible as 4 + 4 > 10 cm.

Chapter Test

Question 1.
In triangles ABC and DEF, ∠A = ∠D, ∠B = ∠E and AB = EF. Will the two triangles be congruent? Give reasons for your answer.
Solution:

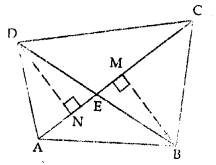
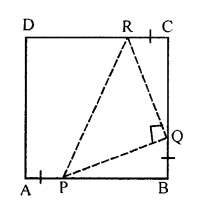
Question 2.
In the given figure, ABCD is a square. P, Q and R are points on the sides AB, BC and CD respectively such that AP= BQ = CR and ∠PQR = 90°. Prove that
(a) ∆PBQ ≅ ∆QCR
(b) PQ = QR
(c) ∠PRQ = 45°

Solution:

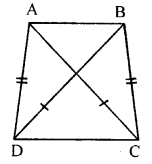
Question 3.
In the given figure, AD = BC and BD = AC. Prove that ∠ADB = ∠BCA.
Solution:

Question 4.
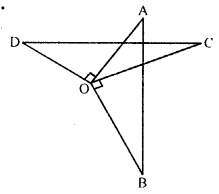
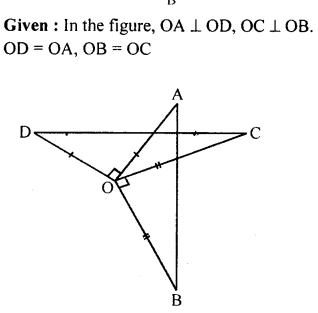
In the given figure, OA ⊥ OD, OC X OB, OD = OA and OB = OC. Prove that AB = CD.

Solution:

Question 5.
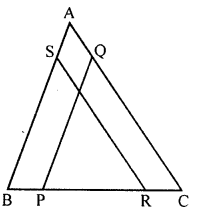
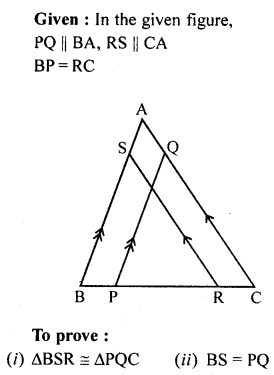
In the given figure, PQ || BA and RS CA. If BP = RC, prove that:
(i) ∆BSR ≅ ∆PQC
(ii) BS = PQ
(iii) RS = CQ.

Solution:

Question 6.
In the given figure, AB = AC, D is a point in the interior of ∆ABC such that ∠DBC = ∠DCB. Prove that AD bisects ∠BAC of ∆ABC.
Solution:

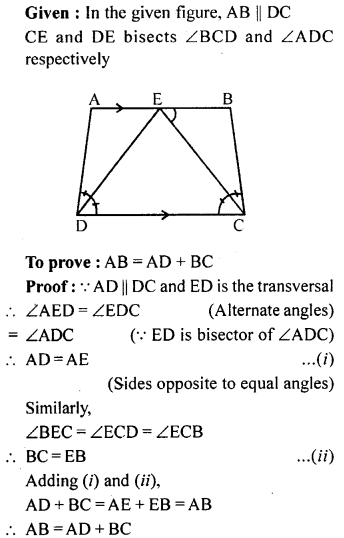
Question 7.
In the adjoining figure, AB || DC. CE and DE bisects ∠BCD and ∠ADC respectively. Prove that AB = AD + BC.
Solution:

Question 8.
In ∆ABC, D is a point on BC such that AD is the bisector of ∠BAC. CE is drawn parallel to DA to meet BD produced at E. Prove that ∆CAE is isosceles
Solution:

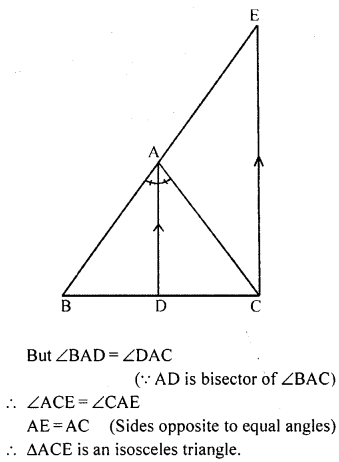
Question 9.
In the figure (ii) given below, ABC is a right angled triangle at B, ADEC and BCFG are squares. Prove that AF = BE.

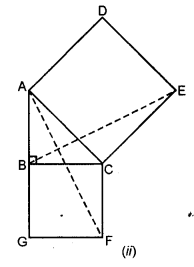
Solution:

Question 10.
In the given figure, BD = AD = AC. If ∠ABD = 36°, find the value of x .

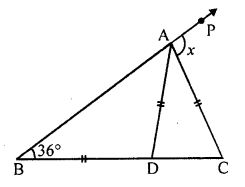
Solution:

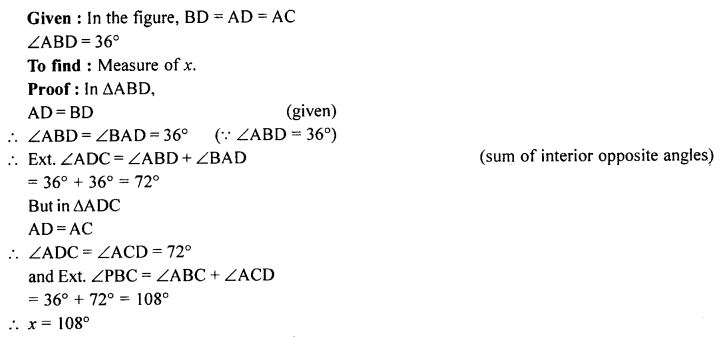
Question 11.
In the adjoining figure, TR = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that RB = SA.

Solution:
Given: In the figure , RST is a triangle

Question 12.
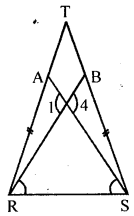
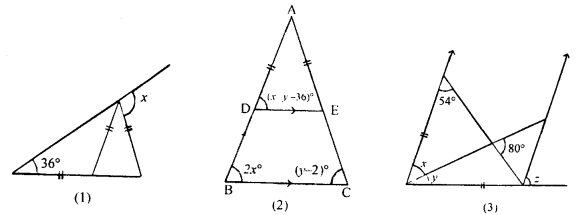
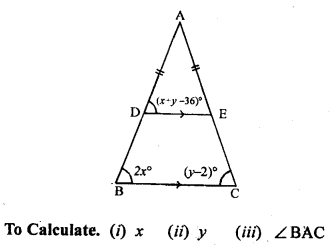
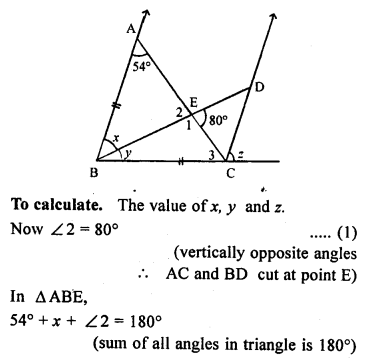
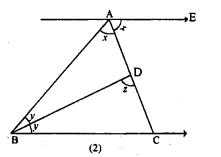
(a) In the figure (1) given below, find the value of x.
(b) In the figure (2) given below, AB = AC and DE || BC. Calculate
(i)x
(ii) y
(iii) ∠BAC
(c) In the figure (1) given below, calculate the size of each lettered angle.

Solution:

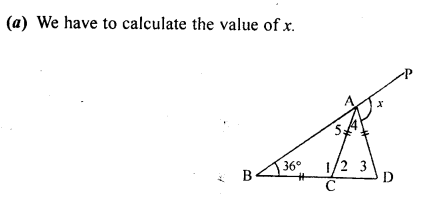
Question 13.
(a) In the figure (1) given below, AD = BD = DC and ∠ACD = 35°. Show that
(i) AC > DC (ii) AB > AD.
(b) In the figure (2) given below, prove that
(i) x + y = 90° (ii) z = 90° (iii) AB = BC

Solution:

Question 14.
In the given figure, ABC and DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that
(i) ∆ABD ≅ ∆ACD
(ii) ∆ABP ≅ ∆ACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC.
Solution:

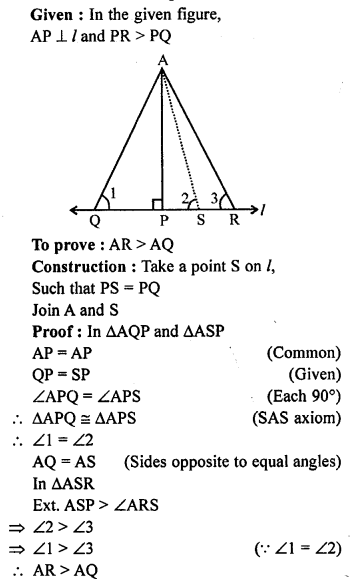
Question 15.
In the given figure, AP ⊥ l and PR > PQ. Show that AR > AQ.
Solution:

Question 16.
If O is any point in the interior of a triangle ABC, show that
OA + OB + OC > \(\frac { 1 }{ 2 }\)
(AB + BC + CA).

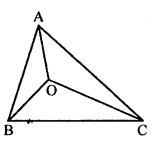
Solution:

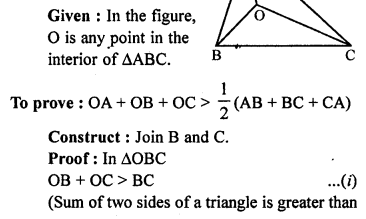
Question P.Q.
Construct a triangle ABC given that base BC = 5.5 cm, ∠ B = 75° and height = 4.2 cm.
Solution:

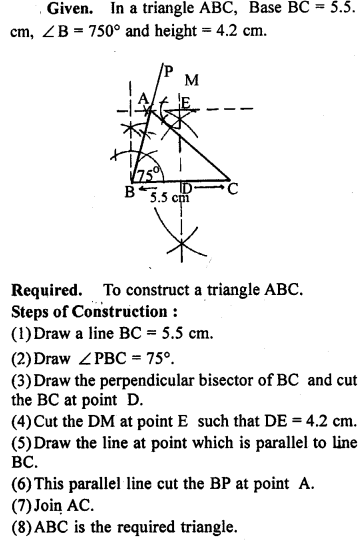
Question P.Q.
Construct a triangle ABC in which BC = 6.5 cm, ∠ B = 75° and ∠ A = 45°. Also construct median of A ABC passing through B.
Solution:

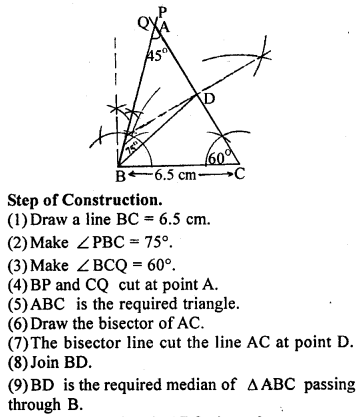
Question P.Q.
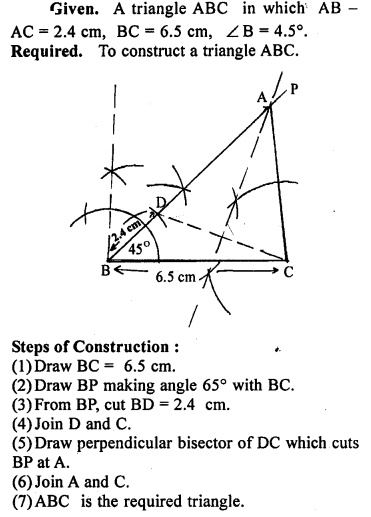
Construct triangle ABC given that AB – AC = 2.4 cm, BC = 6.5 cm. and ∠ B = 45°.
Solution: