A Plus Topper

Improve your Grades

Math Labs with Activity - Out of Two Chords, Larger is Nearer to the Centre of Circle

by

Math Labs with Activity – Out of Two Chords, Larger is Nearer to the Centre of Circle

OBJECTIVE

To verify that out of two chords of a circle, the larger one is nearer to the centre of the circle

Materials Required

  1. A sheet of transparent paper
  2. A geometry box

Theory
The theorem can be proved as shown below.
Consider a circle with centre O and radius r, having two chords AB and PQ.such that AB > PQ. Join AO and PO. Draw the perpendicular bisectors OM and ON of the chords AB and PQ respectively (as shown in Figure 26.1).
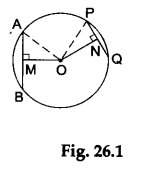
Math Labs with Activity - Out of Two Chords, Larger is Nearer to the Centre of Circle 1
Since AB > PQ, we have
½ AB > ½ PQ, i.e., AM > PN  … (i)
In the right-angled ΔAMO, we have
AO² = AM² + OM² … (ii)
and, in the right-angled ΔPNO, we have
PO² = PN² + ON² … (iii)
From equations (ii) and (iii), we get
AM² + OM² =PN² + ON²
[∴ AO = PO = r =>AO² = PO²] => AM² + OM² < AM² + ON² [using equation (i)]
=> OM² < ON²
=> OM < ON.
Thus, distance of the chord AB from O < distance of the chord PQ from O.

Procedure
Step 1: Mark a point O on the sheet of transparent paper. With O as the centre, draw a circle of any radius.
Step 2: Place the needle of a pair of compasses at any point A on the circle and taking any radius draw an arc cutting the circle at a point, say, B. Join AB. Then, AB is a chord of the circle.
Step 3: Now, slightly reduce the radius of the compasses. Again, place the needle of the compasses at any point P on the circle and draw an arc cutting the circle at a point, say, Q. Join PQ. Then, PQ is a chord of the circle such that AB > PQ.
Step 4: Draw the perpendicular bisectors OM and ON of the chords AB and PQ respectively. (To draw the perpendicular bisectors, adopt the procedure discussed in Activity 25.) The diagram will appear as shown in Figure 26.2.
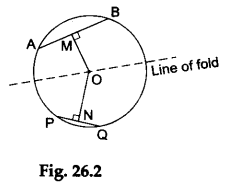
Math Labs with Activity - Out of Two Chords, Larger is Nearer to the Centre of Circle 2
Step 5: Fold the paper along the line that passes through the centre O of the circle such that OM overlaps ON.

Observations
We observe that when the paper is folded, the point M falls at some point on the line ON. This shows that OM < ON, i.e., the distance of the chord AB (larger chord) from the centre O is less than the distance of the chord PQ (smaller chord) from the centre O.

Result
It is verified that out of two chords of a circle, the larger one is nearer to the centre.

Remarks:
From the theorem verified above, it follows that the diameter is the longest chord in a circle since it is nearer to the centre than any other chord.

Math Labs with ActivityMath LabsScience Practical SkillsScience Labs