Math Labs with Activity - Sum of the First n Terms of an AP

Math Labs with Activity – Sum of the First n Terms of an AP

OBJECTIVE

To verify that the sum of the first n terms of an arithmetic progression where a is the first term and d is the common difference is given by

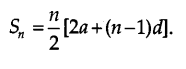
Materials Required

1. A sheet of white paper
2. A geometry box
3. A tube of glue
4. A long, colored paper tape of uniform width (say, 1 unit)
5. A pencil

Theory
If a is the first term, d the common difference and l the nth term of an AP then
l=a + (n-1)d. … (i)
Now, the sum of n terms of an AP is given by

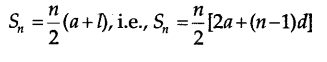
[using equation (i)].

Procedure
Step 1: We shall verify the above formula for a general AP having the first term a and the common difference d for n = 10.
Step 2: Draw horizontal lines on the sheet of paper with a distance of 1 unit between two consecutive lines.
Step 3: Cut 10 small rectangular strips from the coloured paper tape, each of the same length (say, a units).
Step 4: Cut 45 other small rectangular strips from the paper tape, each of the same length (say, d units).
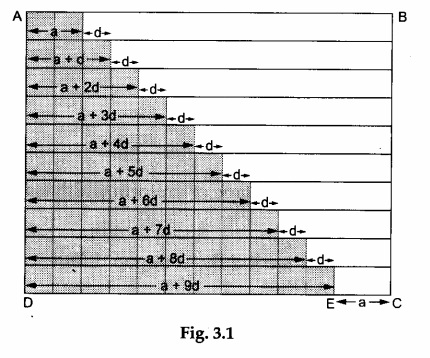
Step 5: Paste both types of strips on the white paper along the horizontal lines so as to obtain rectangles of lengths a,a + d,a + 2d,…,a+9d arranged sequentially, as shown in Figure 3.1.
Step 6: Extend the line DE to C by a units to construct the rectangle ABCD (as shown in Figure 3.1).
Step 7: Cut the portion of the rectangle ABCD which is covered with the coloured paper tape. We find that this portion completely covers the remaining portion of the rectangle ABCD.

Observations and Calculations

1. The length of the rectangle ABCD = (a + 9d) + a = 2a + 9d and the breadth of the rectangle ABCD =10×1=10 units.
   ∴  the area of the rectangle ABCD = 10(2a + 9d) units² … (ii)
2. Area of the portion of the rectangle ABCD covered with coloured strips of paper tape = sum of the areas of the 10 rectangles
   = (a x 1) + [(a + d) x 1] + [(a + 2d) x 1]+…+ [(a + 9d) x 1]
   = a+(a + d)+(a + 2d) +…+ (a + 9d). … (iii)
3. Area of the portion of the rectangle ABCD covered by the coloured strips = ½ (area of the rectangle ABCD).
   a + (a + d)+(a + 2d) +…+(a + 9d) = 10/2 (2a + 9d) [using equations (ii) and (iii)]
   i.e., a + (a + d) + (a + 2d) +…+ [a + (n -1 )d] = n/2 [2a+(n -1 )d] for n = 10.

Result
It is verified for n = 10 that the sum of the first n terms of an AP is given by

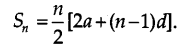
Remarks:
The students shall apply the above method of verification for various values of n, taking different values of a and d as well.

Math Labs with ActivityMath LabsScience Practical SkillsScience Labs

Math Labs with ActivityMath LabsScience Practical SkillsScience Labs