Math Labs with Activity - Sequence of Numbers is an Arithmetic Progression (AP)

Math Labs with Activity – Sequence of Numbers is an Arithmetic Progression (AP)

OBJECTIVE

To verify using a graphical method that a given sequence of numbers is an arithmetic progression (AP)

Materials Required

1. 1. Two sheets of graph paper
   2. A ruler
   3. A pencil
   4. A long, colored paper tape of uniform width (say, 1 unit)
   5. A tube of glue

Theory
A sequence of numbers in which every term except the first term is obtained by adding a fixed number to its preceding term is called an arithmetic progression (AP).

Procedure
Step 1: Mark both the sheets of graph paper with squares (each side = 1 unit).
Step 2: Mark x- and y-axes on each sheet of graph paper.
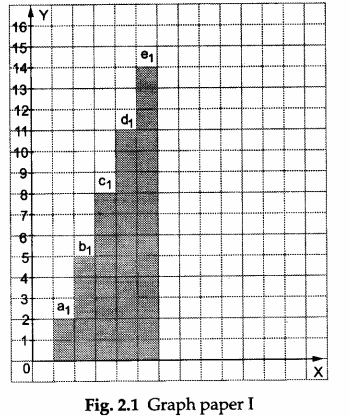
Step 3: We shall first test if the sequence 2,5,8,11,14,… is an AP.
Step 4: Cut the paper tape in rectangular strips of lengths 2 units, 5 units, 8 units, 11 units, 14 units,….
Step 5: Using the x-axis as the base, paste the strips on graph paper I sequentially (as shown in Figure 2.1). Record your observations in the first observation table.

Step 6: We shall now test if the sequence 2,6,9,13,16,… is an AP.
Step 7: Cut the paper tape in rectangular strips of lengths 2 units, 6 units, 9 units, 13 units, 16 units,….

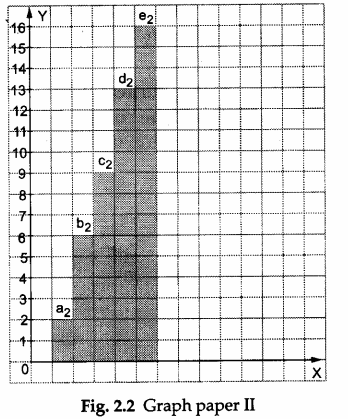
Step 8: Using the x-axis as the base, paste the strips on graph paper II sequentially (as shown in Figure 2.2). Record your observations in the second observation table.

Observations
I. For Figure 2.1

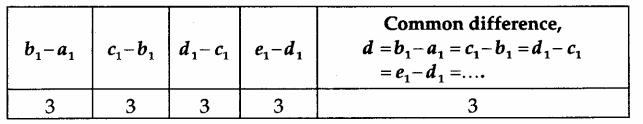
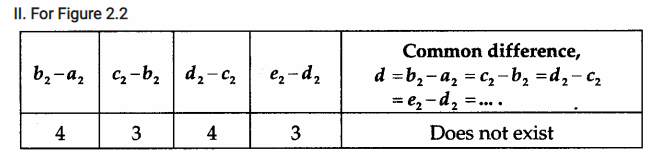
Conclusions

1. The sequence 2, 5, 8, 11, 14, … forms a uniform ladder having equal steps (as shown in Figure 2.1) and has a common difference d = 3 units (see the first observation table). Hence, this sequence is an AP.
2. The sequence 2,6,9,13,16,… forms a ladder but of unequal steps (as shown in Figure 2.2) and the common difference (d) does not exist (see the second observation table). Hence, this sequence is not an AP.

Math Labs with ActivityMath LabsScience Practical SkillsScience Labs