Math Labs with Activity - Perpendicular Drawn from Centre of a Circle to Bisect a Chord

Math Labs with Activity – Perpendicular Drawn from Centre of a Circle to Bisect a Chord

OBJECTIVE

To verify that the perpendicular drawn from the centre of a circle to a chord bisects the chord.

Materials Required

1. A sheet of white paper
2. A geometry box
3. A sheet of tracing paper
4. A piece of cardboard
5. A tube of glue

Theory
The theorem can be proved as below.
Consider a circle with centre O and radius r having a chord AB. Let OL be the perpendicular drawn from the centre of the circle to the chord AB. Join OA and OB (see Figure 18.1).

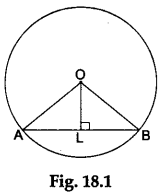
In ΔAOL and BOL, we have

1. OA = OB (each equal to r)
2. OL =OL (common)
3. ∠OLA = ∠OLB (each equal to 90°)

Therefore, ΔAOL is congruent to ΔBOL (by RHS-criterion).
So, LA = LB, i.e., L is the midpoint of AB.

Procedure
Step 1: Paste the sheet of white paper on the cardboard and mark a point O on this paper. With O as the centre, draw a circle with any radius.
Step 2: Draw a chord AB in this circle.
Step 3: Trace the circle along with the chord AB on the tracing paper.
Step 4: Fold the tracing paper along a line which passes through the centre O of the circle and also cuts the chord AB such that the part of the chord that lies on one side of this line overlaps the part on the other side.
Form a crease and unfold the tracing paper. Draw a line OL over the crease such that the point L lies on the chord AB, as shown in Figure 18.2. Then, OL is the perpendicular drawn from the centre of the circle to the chord AB.

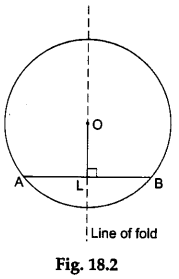
Step 5: Now fold the tracing paper along the line OL.

Observations
We observe that when the tracing paper is folded along the line OL, the point A lies exactly over the point B. This shows that AL = LB, i.e., L is the midpoint of AB, i.e., OL bisects the chord AB.

Result
It is verified that the perpendicular drawn from the centre of a circle to a chord bisects the chord.

Math Labs with ActivityMath LabsScience Practical SkillsScience Labs