Math Labs with Activity - Lateral Surface Area of a Right-Circular Cone Formula

Math Labs with Activity – Lateral Surface Area of a Right-Circular Cone Formula

OBJECTIVE

To demonstrate a method to derive a formula for finding the lateral surface area of a right-circular cone (Method 1).

Materials Required

1. A model of a right-circular cone made of chart paper
2. A sheet of white paper
3. A coloured glazed paper
4. A geometry box
5. A pair of scissors
6. A roll of Sellotape

Theory
A right-circular cone is formed by folding a sector of a circular sheet of paper. When such a cone of slant height l and base radius r (as shown in Figure 33.1) is unfolded,

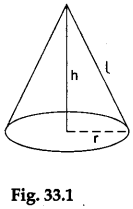
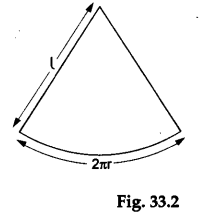
we get a sector of a circular sheet of radius l formed by an arc of length 2πr (as shown in Figure 33.2).

Procedure
Step 1: Take the model of the right-circular cone. Mark a point P on its circular edge. Mark its vertex as O.
Join OP and measure it. Let the length of OP be l (see Figure 33.3).

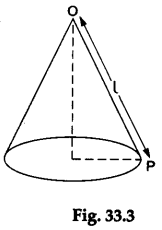
Then, the slant height of the cone is l.
Step 2: Place the cone over the sheet of white paper. Use a pencil and draw along the edge of the circular base of the cone to get a circle on the white paper. Determine the centre of this circle (by applying the method discussed in Activity 21). Mark it X. Take a point Y on the circumference of this circle. Join XY and measure it. Let this be r (see Figure 33.4).

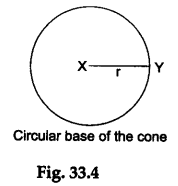
Then, the radius of the base of the cone is r.
Step 3: Mark a point O’ on the coloured glazed paper. Taking O’ as the centre, draw a circle of the radius l. Mark a point P’ on this circle.
Step 4: Calculate 2πr taking π = 22/7 and using the value of r measured in Step 2. Tate a thread of length 2πr. Place its one end at the point P’ and move it along the circumference of the circle. Mark the point Q’ on the circle where the thread has its other end. Cut the sector P’OQ’ from the glazed – paper as shown in Figure 33.5.

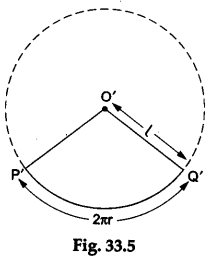
Step 5: Calculate the surface area of the sector drawn on the glazed paper (see Calculations).
Step 6: Fold the sector cut from the glazed paper so that the line O’P’ lies exactly over the line O’Q’. Join the two ends of the sector by Sellotape. Place this cone over the model cone. What do you observe?

Observations
We observe that the cone formed by folding the sector exactly covers the model cone.
Therefore, the curved area of the model cone = area of the sector used to form the cone.

Calculations
To find the area of the sector of the circle forming the cone, we proceed as follows.
Length of the arc P’Q’ = 2πr.

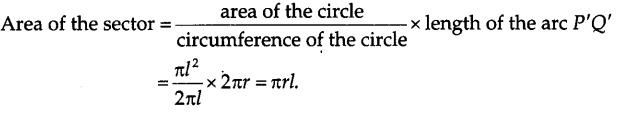
∴ curved area of the model cone = πrl.

Result
The curved surface area of a right-circular cone having slant height l and radius of the base r is given by πrl.

Remarks:
The total surface area of a right-circular cone can be determined by adding the area of its circular base, πr², to the curved surface area, πrl.
Thus, total surface area of the cone = πrl + πr² = πr(l+r).

Math Labs with ActivityMath LabsScience Practical SkillsScience Labs