Math Labs with Activity – Incircle of a given Triangle by Paper Folding Method
OBJECTIVE
To draw the incircle of a given triangle by the method of paper folding
Materials Required
- A sheet of white paper
- A geometry box
Theory
The point of intersection of the internal bisectors of the angles of a triangle gives the incentre of the triangle.
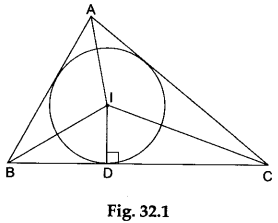
Let I be the incentre of a ΔABC. We drop a perpendicular from I on the side BC. Let ID ⊥ BC.
Taking I as the centre and ID as the radius, we can draw the incircle of the ΔABC (see Figure 32.1).
Procedure
Step 1: Draw any triangle on the sheet of white paper.
Mark its vertices as A, B and C. We shall draw the incircle of the ΔABC.
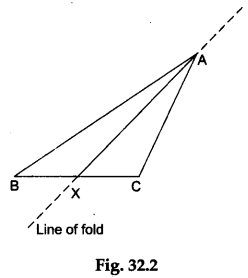
Step 2: Fold the paper along the line passing through the vertex A such that the side AB falls over the side AC. Make a crease and unfold the paper.
Draw a line AX along the crease. Then, AX is the internal bisector of ∠A as shown in Figure 32.2.
Step 3: Fold the paper along the line passing through the vertex B such that the side BC falls over the side AB. Make a crease and unfold the paper. Draw a line BY along the crease. Then, BY is the internal bisector of ∠B as shown in Figure 32.3.
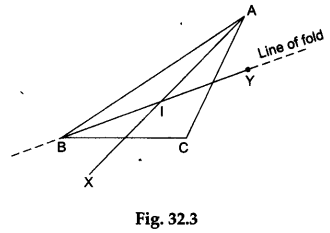
Step 4: Mark the point of intersection of the two angle bisectors as the point I.
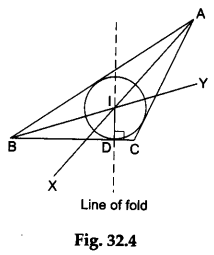
Step 5: Fold the paper along the line that passes through the point I and cuts the line BC in such a way that one part of the line BC falls over the other part. Make a crease and unfold the paper. Mark a point D where the line of fold cuts the line BC. Join ID as shown in Figure 32.4.
Step 6: Taking / as the centre and ID as the radius, we draw a circle (using a pair of compasses) as in Figure 32.4.
Result
The circle drawn in Figure 32.4 is the incircle of the given triangle.
Remarks: The teacher must explain it to the students that since all the angle bisectors of a triangle meet at a point, it is sufficient to construct only two angle bisectors so as to obtain their point of intersection as the incentre.
Math Labs with ActivityMath LabsScience Practical SkillsScience Labs