Math Labs with Activity – Complete a Circle if an Arc of the Circle is Given
OBJECTIVE
To complete a circle if an arc of the circle is given.
Materials Required
- A sheet of transparent paper
- A geometry box
- A bangle
Theory
If an arc of a circle is given, we can draw two chords by taking three points on this arc (see Figure 22.1).
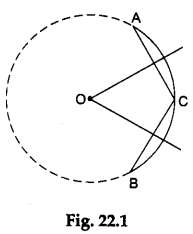
Now, using the concept (same as that used in Activity 21) that the perpendicular bisectors of two chords of a circle intersect at the centre of the circle, the centre of the circle can be determined.
Taking a point on the arc and joining it to the centre we get the radius of the circle, and thus the circle can be constructed.
Procedure
Step 1: Place the bangle on the sheet of transparent paper and using this bangle draw an arc AB. Now, we have to draw the circle having the arbitrary arc AB as part of its circumference.
Step 2: Mark a point C anywhere on the arc AB. Join AC and CB. Then, AC and CB are two chords of the circle.
Step 3: Fold the paper along the line which cuts the chord AC in such a way that the point A lies exactly over the point C. Form a crease and unfold the paper. On this crease, draw a line PQ.
Then, PQ is the perpendicular bisector of the chord AC.
Step 4: Again fold the paper along a line which cuts the chord CB in such a way that the point C lies exactly over the point B. Form a crease and unfold the paper.
On this crease, draw a line MN. Then, MN is the perpendicular bisector of the chord CB.
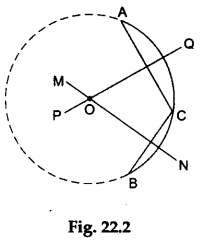
Step 5: The point of intersection, O, of the lines PQ and MN gives the centre of the circle. Join OA. With O as the centre and radius OA, draw a circle.
Result
The circle thus obtained is the required circle.
Math Labs with ActivityMath LabsScience Practical SkillsScience Labs