A Plus Topper

Improve your Grades

Math Labs with Activity - Chords of a Circle which are Equidistant from Centre of Circle

by

Math Labs with Activity – Chords of a Circle which are Equidistant from Centre of Circle

OBJECTIVE

To verify that the chords of a circle which are equidistant from the centre of the circle are equal.

Materials Required

  1. A sheet of transparent paper
  2. A geometry box

Theory
The theorem to be verified is the converse of the theorem verified in Activity 23.

Procedure
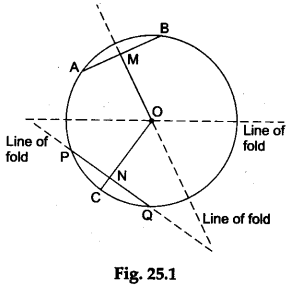
Step 1: Mark a point O on the sheet of transparent paper. Draw a circle with centre O taking any radius.
Step 2: Draw any chord AB in the circle. Fold the paper along the line that passes through the centre O of the circle and cuts the chord AB such that one part of the chord AB overlaps the other part.
Make a crease and unfold the paper. Mark the point M where the line of fold cuts the chord AB. Join OM.
Then, OM is the perpendicular bisector of the chord AB and gives the distance of the chord AB from the centre O of the circle.
Step 3: Draw any radius OC. On this radius OC, mark a point N such that OM = ON.
Step 4: Fold the paper along the line that passes through the point N such that NC overlaps NO. Make a crease and unfold the paper.
Mark the points P and Q where the line of fold cuts the circle. Join PQ.
Then, PQ is a chord of the circle whose distance from the centre O of the circle is ON, which is equal to the distance OM of the chord AB from the centre O of the circle (see Figure 25.1).
Step 5: Fold the paper along the line which passes through the centre O of the circle such that OM overlaps ON.
Math Labs with Activity - Chords of a Circle which are Equidistant from Centre of Circle 1

Observations

  1. OM exactly covers ON since OM = ON.
  2. AB exactly covers PQ. This shows that the chord AB is equal to the chord PQ.

Result
It is verified that the chords of a circle which are equidistant from the centre of the circle are equal.

Math Labs with ActivityMath LabsScience Practical SkillsScience Labs