Math Labs with Activity - Angles Subtended by an Arc of a Circle in the Same Segment

Math Labs with Activity – Angles Subtended by an Arc of a Circle in the Same Segment

OBJECTIVE

To verify that the angles subtended by an arc of a circle in the same segment of the circle are equal

Materials Required

1. A sheet of white paper
2. A piece of cardboard
3. A sheet of tracing paper
4. A geometry box
5. A tube of glue

Theory
The theorem can be proved as follows.
Consider a circle with centre O and radius r.
Let ∠ACB and ∠ADB be two angles made by an arc AB in the same segment ΔCDB of the circle, as shown in Figure 28.1. Join AO and BO.

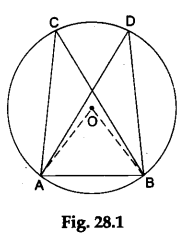
Then, by the theorem verified in Activity 27, we have
∠AOB = 2 ∠ACB and ∠AOB = 2 ∠ADB.
:. 2∠ACB = 2∠ADB i.e., ∠ACB = ∠ADB.

Procedure
Step 1: Paste the sheet of white paper on the cardboard.
Mark a point O on this paper. With O as centre, draw a circle of any radius.
Step 2: Mark two points A and B on the circle. Then, AB is an arc of the circle.
Mark two points C and D on the circle in the same segment. Join CA, CB, DA and DB.
Step 3: Then, ∠ACB and ∠ADB are the angles subtended by AB in the same segment of the circle, as shown in Figure 28.2.

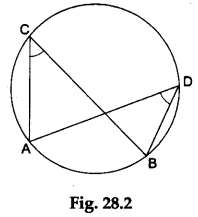
Step 4: Trace ∠ADB on the tracing paper and label it ∠A’D’B’.
Step 5: Place ∠A’D’B’ over ∠ACB such that D’B’ lies over AC, the point D’ lies over point B, and A’D’ lies over BC as shown in Figure 28.3.

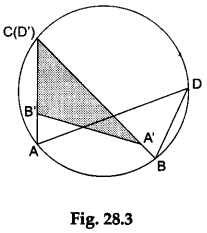
Observations
We observe that ∠A’D’B’ exactly covers ∠ACB.
∴ ∠ACB = ∠ADB [∴ ∠A’D’B’ is same as ∠ADB].

Result
It is verified that the angles subtended by an arc of a circle in the same segment of the circle are equal.

Remark:
The teacher must ask the students to verify the above result for the angles subtended by an arc in the same segment for the arcs equal to or greater than the semicircle.

Math Labs with ActivityMath LabsScience Practical SkillsScience Labs