Kerala SSLC Maths Previous Question Papers with Answers 2017 are part of Kerala SSLC Maths Previous Year Question Papers with Answers. Here we have given Kerala SSLC Maths Previous Question Papers with Answers 2017.
| Board | SCERT |
| Class | SSLC Class 10 |
| Subject | Maths |
| Category | Kerala SSLC Previous Question Papers |
Kerala SSLC Maths Previous Question Papers with Answers 2017 Free Download English Medium
Time Allowed: 2 1/2 hours
Cool off time: 15 Minutes
Maximum Marks: 80
Instructions
- Read each question carefully before writing the answer.
- Give explanations wherever necessary.
- First 15 minutes is cool-off time.
- No need to simplify irrationals like √2, √3, π etc. using approximations unless you are asked to do so.
- Simplification of irrationals like √2, π, etc with their approximate values is not required it not specified on
the question.
Question 1.
Write down the first three forms of the sequence of natural numbers leaving remainder 1 On division by 5. Check whether 510 is a term of above sequence.
Question 2.
Check whether x – 3 is a factor of the polynomial 2x3 – x2 -3x + 4
Question 3.
Heights (in centimeters) of some students in a class are given below
135, 120, 148, 153, 124, 122, 150, 147 Find the median of the heights
Question 4.
Find the area of the triangle whose sides are 30, 50, 60 centimetres.
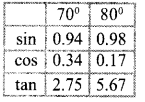
Question 5.
Angle measurement of a triangle are 30°, 70°, 80° If thelenth of its smallest side is 10 centimetrs.
Find the lengths of its other sides. You can use the following table.
Question 6.
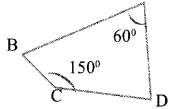
In the figure AB = AD, ∠A = 60°, ∠C = 150° Show that the circle, centred at A and radius AB
a) passes through the point D
b) passes through the point C B
Question 7.
Sum of a number and is reciprocal is 25/12 . Find the number.
Question 8.
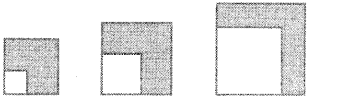
In these figures, the sides of the smaller squares are in the arithmetic sequence 2, 5, 8,……….. and the sides of
the larger squares are in the arithmetic sequence 5,8,11………….
a) Write down the algebrac form of each sequence
b) Write down the algebrac form of the sequence of areas of the shaded portion in each figure.
Question 9.
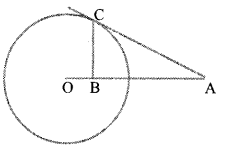
In the figure AC is largest to the circle centered at O.and OB is the perpendicular from C to OA. If the radius of the circle is. r show that OA x OB = r2.
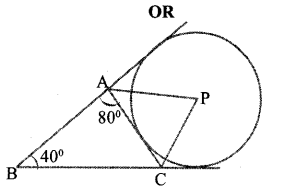
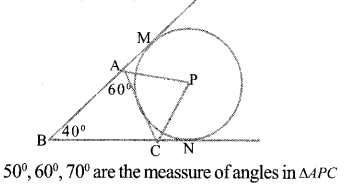
In the figure, P is the centre of an excircle of triangle ABC .If ∠ABC=40°and ∠BAC=80° Find the angle measurement of triangle APC.
Question 10.
The table below shown the workers in a factory sorted according to their daily wages.
| Daily wages (Rs) | Number of workers |
| 400 – 500 | 3 |
| 500 – 600 | 5 |
| 600 – 700 | 9 |
| 700 – 800 | 10 |
| 800 – 900 | 6 |
| 900- 1000 | 2 |
Calculate the median daily wage.
Question 11.
Find the quotient and remainder on dividing the polynomial P (x) = x3 + 5x2 + 2x – 6 by x + 2
Question 12.
The sides of a rectangular prism are 4, 6, 10 centimetres.
a) What is the maximum volume of a square pyramid which can be curved out from this prism.
b) Find the maximum volume of a sphere which can be curved out from the prism.
Question 13.
A cone of height 8 centimetres is to be made using a sector of circle of radius 10 centimetres
a) What should be the central angle of the sector?
b) Calculate the volume and curved surface area of the cone.
Question 14.
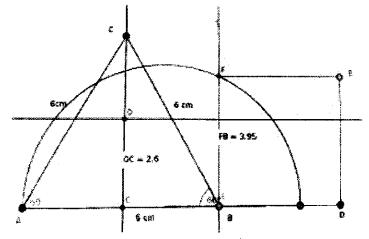
Draw an equilateral triangle of sides 6 centimetres. Draw a square of the same area.
Question 15.
One is asked to say a three digit number. What is the probabily that
a) all the digits of the number are same?
b) the number is a multiple of 6 ?
Question 16.
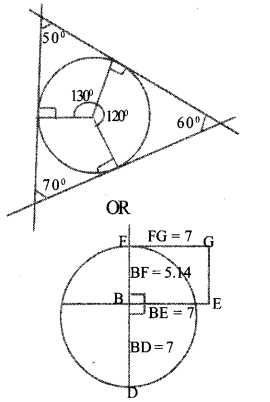
Draw a triangle of angle measures 50°, 60°, 70° and radius of whose incircle is 3centimetres
OR
Draw a rectangle of one side 7 centimetres and area 36 square centimetres.
Question 17.
Length of a rectangle is 20 centimetres and its breadth is 4 centimetres. When a new rectangle is formed by changing the length and breadth, its perimeter decreased by 8 centimetres and area increased by 16 square centimetres. Find the change in its length and breadth.
Question 18.
The first figure above is an equlateral triangle of side 2 centimetres. The second figure is obtained by drawing lines passing through the vertices and parallel to the sides of the triangle in the first figure. The third figure is got by drawing lines passing through the vertices and paeallel to the sides of the triangle in the second figure.
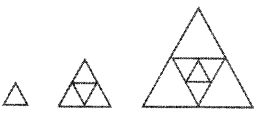
a) Write the sequence of perimetres of biggest triangle in each figure obtained by continuing this process.
b) Write the sequence of areas of biggest triangle in each figure
c) algebraic forms of both of the above sequences.
OR
The first term of an arithmetic sequence is 2 and the common differences is 2 and the common differences is
a) Find the sum of the first ten terms of this sequence.
b) Find the sum of the ten terms from the second term to the eleventh term.
c) Is it possible that the sum of any consecutive ten terms of the sequence is 500 ? Why ?
Question 19.
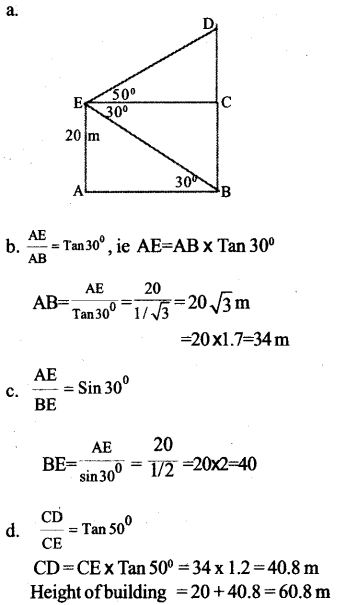
A boy, standing on the top of tower 20 meters height, saw the top of a building at an elevation of 50° and its
base at a depression of 30°. 5
a) Draw a tough figure according to the given data.
b) Find the distance between the flower and the building.
c) Find the distance from the top of the flower to the base of the building.
d) Find the height of the building.
[Use sin 50° = 0.77, cos 50° = 0.64, tan 50° =1.2, √3= 1.7 ]
Question 20.
a. Draw coordinate axes and mark the point (2, 4). Draw the circle of radius 4 units centred at the above point. 5
b. Find the coordinates of the point at which the circle touches the x axis.
c. Calculate the coordinates of the points at which the circle cuts the y axis.
Question 21.
a. Find the centre of the circle with the line joining the points (3, -1), (13 -9) as diameter. Find the equation of this circle.
b. Show that there is no point on the circle whose x and y coordinates are equal.
Question 22.
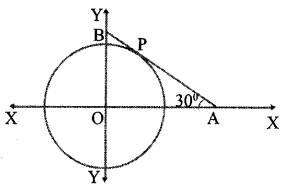
In the figure, the radius of the circle centred at O is 6 units. Line AB touches the circle at P and ∠OAB=30°
a. find the coordinates of the points A and P.
b. find the equation of AB. 5
OR
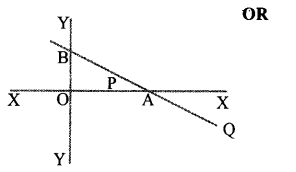
In the figure, equation of the line joining the points A and B is x + 2y = 10. P and Q are points on this line.
a. find the coordinates of the points A and B.
b. find the coordinates of the point P that divides the line AB in the ratio 2:3.
c. if AQ : BQ = 2:3, find the coordinates of the point Q.
ANSWERS
Answer 1.
The first 3 terms having remainder 1 when divided by 5 -1,6,11. 510 is not a term of this sequence because when it is divided by 5 the remainder is not 1 (510 is a multiple of 5).
Answer 2.
P(x) = 2x3 – x2– 3x + 4
P(3) = 2×33 – 32– 3 x 3 + 4 = 40 ≠ 0
i.e, 2x3 – x2 – 3x + 4 4 is not a factor of x – 3
Answer 3.
When the given information is written in ascending order 120, 122, 124, 135, 147, 148, 150, 153.
![]()
Answer 4.
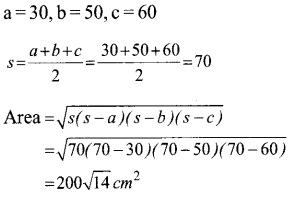
Answer 5.
AB = c = 10 cm, ∠C=30°
![]()
Diameter of in circle = b / SinB
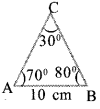
b = Diameter of in circle x Sin 80°
= 20 x 0.98 = 19.6 cm a
= Diameter of in circle x Sin 70°
= 20 x 0.94= 18.8 cm
other sides are 19.6 cm, 18.8 cm a.
Answer 6.
a. GivenAB = AD and ∠A = 60°. When BD is joined ΔABD which is an equilateral triangle is obtained ∠B=60°,∠D=600 The circle drawn with A as the centre and AB as the radius passes through D.
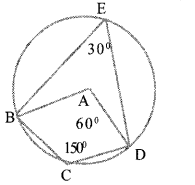
b. Angle of arc BED which is an alternate arc of BCD =1/2 ∠A=30°
∠C +∠E=18° will pass through the circle C.
Answer 7.
The number x and its reciprocal 1/x
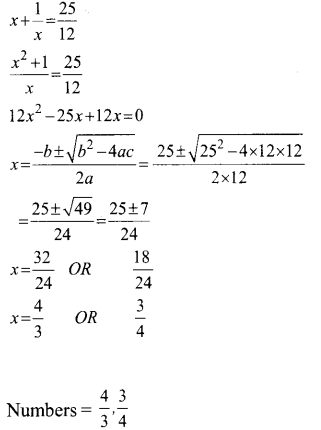
Answer 8.
a. The algebriac form of the sequence 2, 5,
8………. = 3n -1
The algebriac form of the sequence5,
8, 11…………. = 3n + 2
b. The sequence of the coloured part
52 – 22,82 – 52,112 – 82, = 25 – 4,64 – 25,
121-64, ……..= 21,39, ,57…………
Algebriac form = 18n + 3
Answer 9.
In ΔAOC , ΔCOB
∠B = ∠C=90°
∠AOC = ∠BOC
(Same angles)
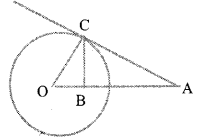
ΔAOC , ΔCOB are similar triangle AO / CO = OC / OB
AO x BO = CO x OC = OC2 AO x BO = r2
OR
In ABAC ∠B=40° ,∠BAC=80°
∠BCA=60°
∠CAM=180°-80° =100°
A4OV=1800 -60° =120°
BA, BC are the tangents of the outer circle. AP is the bisector of ∠ACM in the same way PC is the bisector of ∠ACN.
∠PAC=100 / 2 = 50°
∠PAC=120/ 2=60°
∠P=180-(50+60) 70°
Answer 10.
| Daily wages | Number of workers |
| Below 500 | 3 |
| Below 600 | 8 |
| Below 700 | 17 |
| Below 800 | 27 |
| Below 900 | 33 |
| Below 1000 | 35 |
35 + 1 = 18th worker’s income will be the median income. Median range = 700 – 800.
The income of 10 workers from 18 to 27 will ) be in the range between 700-800.
If 100 rupees in the range between 700 – 800 is divided into 10 equal parts the income of each person will be in this range.
The income of the 18th person will be in be tween 700 and 710.
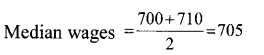
Answer 11.
x3 + 5 x2 + 2x – 6 = (x + 2) ( ax2 + bx+c + d)
= ax3 + bx2 + cx + 2ax2 + 2bx + 2c + d
Comparing the coefficients of x3,1 = a ie a = 1
Comparing the coefficients of x2,5 = b + 2a = b + 2
i.e., b = 5 – 2 =3
Comparing the coefficients of X
2 = c + 2b = c + 6
iec = 2- 6 = -4
Comparing the constant terms
-6 = 2c + d = -8 + d
ie d = -6 + 8 = 2
Quotient = x2 +3x – 4
Remainder = 2
Answer 12.

Answer 13.
Radius of circle = 10 cm
Lateral height of cone = 10 cm
height of cone = 8 cm

Answer 14.
The square BDEF and triangle ABC have the same area
Answer 15.
The total 3 digit numbers = 900
a. 3 digit numbers which have the 3 digits same = 9
Probability of getting 3 digit numbers which have the 3 digits same = 9 / 900 =1/100
b. Smallest 3 digit number which is a multiple of 6= 102
Largest 3 digit number which is a multiple of 6 =996
This is an arithmetic sequence Algebraic form = 6n + 96,6n + 96 = 996 n = 900/6= 150
Number of 3 digit numbers which are multiples of 6= 150
Probability of getting multiples of 6 = 150/900=1/6
Answer 16.
Answer 17.
Length of rectangle = 20 cm
Width of rectangle = 4 cm
Perimeter= 2 x Length + 2 x width = 48 cm
Area = 20 x 4 = 80 cm2
Length of new rectangle = x
Width of new rectangle = y
Perimeter of rectangle = 2 (x + y)
This is lesser than the perimeter of the first rectangle by 8 cm.
ie 2 (x + y) = 48 – 8 = 40 cm
x+y=40/2 = 20 cm, y = 20 – x
area of rectangle = 2 (x + y)
This is greater by 16 cm2 than the perimeter of the first rectangle
ie xy = 80 + 16 = 96 cm2 x2 – 20x + 96 = 0
iex2 – 20x = -96, x2 – 20x +100 = -96 + 100
(x-10)2 = 4, x – 10= ± 2
x = 2 + 10 = 12, x = -2 + 10 = 8
ie Length of new rectangle = 12 cm
Width of new rectangle = 8 cm
Length of the new rectangle (12 cm), lesser
by 8 cm than the first rectangle (12 cm).
Width of the new rectangle (8 cm), 4 cm
greater than the width of the first rectangle (4 cm)
Answer 18.
Length of one side in the first figure = 2 cm Length of one side in the second figure = 4 cm Length of one side in the third figure = 8 cm
a. Sequence of perimeter = 6,12,24,….
b. Sequence of areas =
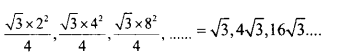
c. Algebriac form of the sequence of perimeters= 6 x 2n-1 = 3 x 2 x 2n-1 = 3 x 2n-1 Algebriac form of the sequence of areas
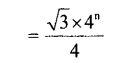
OR
First term = 2, common difference = 4
a. Algebriac form of the sum = 2n2 Sum of the first 10 of the term
= 2 x 102 = 2 x 100 = 200
b. To find the sum of terms from 2 to 11 substract the sum of first 11 terms from the first term.
Sum of first 11 terms=2 x 112 = 2 x 121 = 242
Sum of terms from 2 to 11 = 242 – 2 = 240
c. To find the sum of terms 3 to 12 substract the sum of the first 12 terms from the 22d term = 2 x 122 – 2 – 6
= 288 – 8 = 280
ie. The sum of any 10 consecutive terms of this sequence will be a multiple of 40. Since 500, is not a multiple of 40 it will not be the sum of 10 consecutive terms.
Answer 19.
Answer 20.
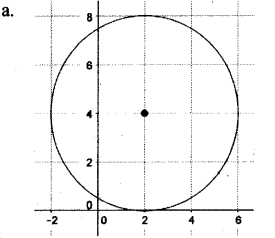
Equation of circle (x – 2 )2 + (y – 4)2 = 42
b. The Y coordinates on X axis will be 0.
(x – 2)2 + (0 – 4)2 = 42
(x – 2)2 = 0, x – 2 = 0, x = 0
ie, the point which touches the axis (2, 0).
c. X coordinates on the Y axis will be 0.
(0 – 2)2+(y – 4)2 = 42
(y – 4)2 = 16 – 4 = 12
y – 4= =± √12 = ± 2 √3
y = 4 ± 2√3
The points which passes through Y axis
(0, 4 + 2 √3 ), (0, 4 -2 √3)
Answer 21.
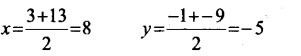
a. The coordinates of the midpoint (8, -5)
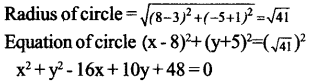
b. If x coordinate and y coordinate are equal x = y
ie x2 + x2 – 16x + 10x + 48 = 0
2x2– 6x + 48 = 0, x2 – 13x + 24 = 0
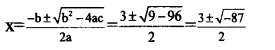
Since negative numbers do not have square root. Numbers with equal values of x and y cannot be found, ie, There are no points in this circle with equal x and y coordinates.
Answer 22.


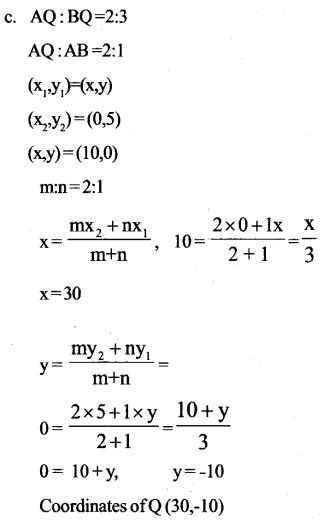
We hope the Kerala SSLC Maths Previous Question Papers with Answers 2017 help you. If you have any query regarding Kerala SSLC Maths Previous Question Papers with Answers 2017, drop a comment below and we will get back to you at the earliest.