Kerala SSLC Maths Model Question Papers with Answers Paper 3 are part of Kerala SSLC Maths Previous Year Question Papers with Answers. Here we have given Kerala SSLC Maths Model Question Papers with Answers Paper 3.
| Board | SCERT |
| Class | SSLC Class 10 |
| Subject | Maths |
| Category | Kerala SSLC Previous Question Papers |
Kerala SSLC Maths Model Question Papers with Answers Paper 3 Free Download English Medium
Time Allowed: 2 1/2 hours
Cool off time: 15 Minutes
Maximum Marks: 80
Instructions
- Read each question carefully before writing the answer.
- Give explanations wherever necessary.
- First 15 minutes is cool-off time.
- No need to simplify irrationals like √2, √3, π etc. using approximations unless you are asked to do so.
- Simplification of irrationals like √2, π, etc with their approximate values is not required it not specified on
the question.
Answer any 3 questions from 1 to 4. Each question carries 2 scores. (Scores 3 x 2 = 6)
Question 1.
The 25th term of an arithmetic sequence is 140 and the 27th term is 166. What is its common difference? What is its 35th term?
Question 2.
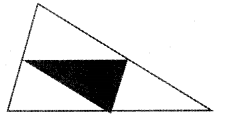
In the figure, the shaded triangle is drawn by joining the mid point of the sides of large triangle calculate the probability of a dot put on larger triangle to be within the shaded triangle.
Question 3.
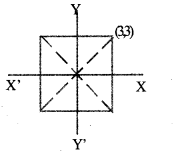
In the figure, the sides of the square are parallel to the axes and the origin is the mid point. Coordinates of one vertex of the square is (3, 3). Write the coordinates of two other vertices of the square.
Question 4.
The ages of 10 members of a club are 20, 25, 22, 32, 42, 27, 35, 27, 35 and 30. Find the median age.
Answer any 5 questions from 5 to 11. Each question carries 3 scores. (Scores 5 x 3 = 15)
Question 5.
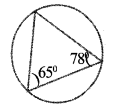
Draw a circle with radius 4 centimetres. Draw a triangle with two of its angles 65° and 78° and all vertices on the circle.
Question 6.
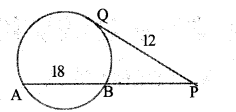
In the figure, the length of the chord AB is 18 centimetre. The chord is extended to P and the tangents drawn from that point have length 12 centimetres. Find the length of BP.
Question 7.
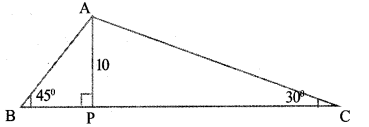
In triangle ABC, thr length of AP is 10 centimetres. What is the length of BP? What is the length of BP? What is the length of PC? Calculate the length of BC.
Question 8.
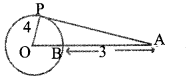
AP is the tangent to the circle with centre at O and radius 4 centimetres. AB = 3 cm. Find the length of OA and the length of the tangent AP.
Question 9.
The radius of two spherical tanks are in the ratio 3 : 4. The volume of the first tank is 540 litres. Find the volume of the second tank.
Question 10.
Write P(x) = x2 – 9x + 20 as a product of two first degree polynomials. Write also the solutions of the equation P(x) = 0
Question 11.
Find the slope of line joining (2, 4) and (4, 7). Write the coordinate of another point on the line. Check whether (5,8) is on this line.
Answer any 7 questions from 12 to 21. Each question carries 4 scores. ( Scores 7 x 4 = 28)
Question 12.
Sum of the first five terms of an arithmetic sequence is 45. What is the third term? The common difference of the sequence is 4. Write the first two terms. Write another arithemetic sequence having the sum of the first five term 45.
Question 13.
Draw a rectangle of area 18 square centimetre. Draw a square of the same area.
Question 14.
From all two digit numbers with each digit 1,2,3,4 or 5 one number is chosen:
a. What is the probability of both digits being the same?
b. What is the probability of the sum of the digits being 8 ?
c. What is the probability that it is a multiple of 5?
Question 15.
In triangle ABC, length of AB = 6 cm, ∠A = 70°, ∠B = 55°
a. Find ∠C
b. Find AC
c. Find the area of triangle ABC (sin 70° = 0.93)
Question 16.
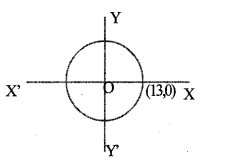
The centre of the circle shown is the origin and radius is 13?
a. Check whether each of the points (12, 5), (10, 6) is inside, outside or on the circle.
b. Write the coordinates of two other points on the circle.
Question 17.
Calculate the area and perimetre of a triangle of sides 30 centimetre, 28 centimetre and 26 centimetre. Also calculate the radius of the incircle.
Question 18.
A square pyramid of base edge 10 centimetres and height 12 centimetres is to be made of paper.
a. Calculate the slant height of the pyramid.
b. What is the area of the paper needed to make square pyramid?
Question 19.
P(x) = ax3 + bx2 + cx + d
a. Find P(-1).
b. If x+1 is a factor of P(x) then prove that a + c = b + d.
c. Write a third degree polynomial having (x+1) as a factor.
Question 20.
In the picture, mid points of the sides of the quadrilateral ABCD are joined to draw PQRS.
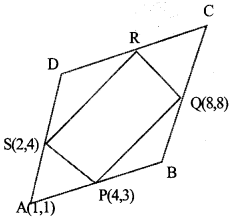
a. Find Coordinates of R.
b. Write Coordinates of all vertices of quadrilateral ABCD.
Question 21.
Some households in a locality are sorted according to their electricity usage in the table below.
| Usage of electricity (Unit) | No. of households |
| 80 – 100 | 8 |
| 100 – 120 | 12 |
| 120 – 140 | 10 |
| 140 – 160 | 9 |
| 160 – 180 | 6 |
a. If the household using the least unit of electricity is numbered as one and the second least as two and so on, what is assumed to be usage of electricity of the 21st household.
b. Calculate the median usage of electricity?
Answer any 5 questions from 22 to 28. Each question carries 5 scores.
Question 22.
a. Find the least and heighest three digit number which leave a remainder 1 on division by 9.
b. How many three digit numbers are there, which leave a remainder one on division by 9?
c. Find the sum of all such numbers.
Question 23.
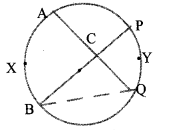
In the circle shown, the chords AQ and BP passes through C.
a. The central angle of arc AXB is 100° calculate ∠Q. The central angle of arc PYQ is 60°. Find all angles of the triangle BQC.
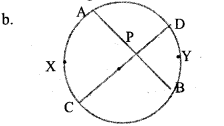
In the picture, prove that ∠APC is half the sum of the central angle of arc AXC and arc BYD.
Question 24.
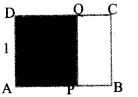
From the rectangle ABCD of breadth 1 metre, the largest possible square APQD is cut off. The remaining rectangle is PBCQ.
a. Taking the length of ABCD as x, write the length and breadth of PBCQ.
b. The ratio of length and breadth of the rectangle, ABCD and PBCQ are same. Find length of AB.
Question 25.
A man standing on the top of a light house sees a ship approaching the seashore at an angle of depression of 22°. After the ship has travelled 100 metres more. Towards the sea shore,he sees it at an angle of depression of 31°. The ship stops there.
a. Draw a rough-sketch.
b. How far is the ship from the light house.
c. Find the height of light house. [tan22° = 0.4, tan31° = 0.6]
Question 26.
Draw a triangle of sides 6 centimetre, 7 centimetre and 8 centimetre. Draw a circle which touches all sides of the triangle and measure its radius.
Question 27.
A cone is made from sector of radius 10 centimetre and central angle 216°.
a. What is slant height and radius of the cone?
b. Find the volume of the cone.
Question 28.
Find the length of line joining A(-2, -3) and B(4, 5). Write the equation of circle whose diameter is AB.
Question 29.
Read the mathematical concept given below carefully and understand it. Then answer the following questions.

Diagonal of a polygon is a line joining two non-adjacent vertices see this tables.

From the above table, we see the relationship between the number of sides of a polygon and the number of diagonals.
Answer the question’s given below:
a. Which polygon has the same number of sides and diagonals?
b. How many diagonals can be drawn from a single vertex of an 8 – sided polygon?
c. How many diagonals does 20 sided polygon have?ch contains many perfect squares.
ANSWERS
Answer 1.
Given 25th term = 140 and 27 h term is 166 a + 24d = 140 and a + 26d = 166 Solve this equations for a and d
Then we get d = 13 and a = -172
35th term = a+34 d=-172+34 x 13
= -172 + 442 = 270
Answer 2.
In the figure, successively joined the mid points of the lager triangle sides being made four equal triangles and its area also be equal. In the figure, shaded area of the triangle be the one fourth area of the larger triangle. Hence the probability of the dot in the Shaded triangle be 1/4.
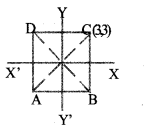
Answer 3.
From the figure, coordinates of B = (3, -3) coordinates of. A = (-3,-3)and coordinates of D = (-3,3)
Answer 4.
Given ages = 20, 25, 22, 32, 42, 27, 35 ,27, 35, and 30
Arrange data in assenting order = 20,22,25, 27,27,30,32,35,35 and 42.
Median =\(\frac { 27+30 }{ 2 } \) = 28.5
Answer 5.
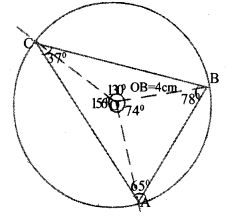
Draw a circle radius OB = 4 cm. Make an angle ∠BOC = 130° (2 ∠B = 2 x 65 = 130) and ∠AOC =156° and marks B and A respectively. Joint AB, BC, CA is the required construction.
Answer 6.
Consider BP = x cm
AP = AB + BP ⇒ 18 + x
AP X BP = PQ2
⇒ (18 + x) x = 122
⇒(18x + x2) = 144
⇒ x2 + 18x – 144 = 0
⇒ (x-6) (x + 24) = 0
ie., x = 6 or x = -24; -24 is rejected because -24 is not become the measurement of a line.
Hence x = 6
BP = 6 cm
Answer 7.
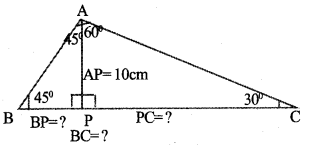
In the given figure we can understand that triangle APB be an isosceles triangle. So the base angle ∠B = ∠A = 45° each.
AP = BP = 10 cm (Give AP = 10 cm)
ie.,BP = 10 cm
In the figure right angled triangle APC,

Answer 8.
From the figure OP = 4 cm (given radius)
ie.,OP = OB = 4 cm
OA = OB + AB = 4 + 3 = 7 cm
ΔAPO be right angled triangle, right angle at P (tangent theorem) By Pythagoras,
AP2 – OA2 = 72 – 42 = 49 – 16 = 33
AP = √33
Answer 9.
Ratio of the radii = 3 : 4.
ie., r1 : r2 = 3x : 4x
Volume of the first tank (V1) = 540
Let the volume of the Second tank be V2 Volume of the first tank
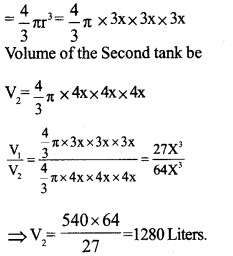
Answer 10.
Given P(x) = x2 – 9x + 20
Product of two first degree polynomial
= (x – 5) (x – 4)
Solution of the polynomial, Given P(x) = 0
ie., (x – 5) (x – 4)=0 (Using zero factor theorem)
Either x – 5 = 0 or x – 4 = 0
ie., x = 5 or x = 4
Hence the solution be 5 or 4
Answer 11.

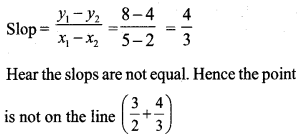
Answer 12.
Given the sum of the first five term of an AP =45
Common difference = 4
Third term is its middle term
sum = middle term x number of term
![]()
ie., Second term=third term – common difference = 9 – 4 = 5
First term = Second term – common difference = 5 – 4 = 1
The first two terms = 1 and 5.
If the sum of the first five term of an AP is 45, then the third term should be 9 but the common difference may be changed. In this condition we can make many AP’s.
Hence The AP = 5, 7, 9, 11, 13,………
or = 3, 6, 9, 12, 15,………….
Answer 13.
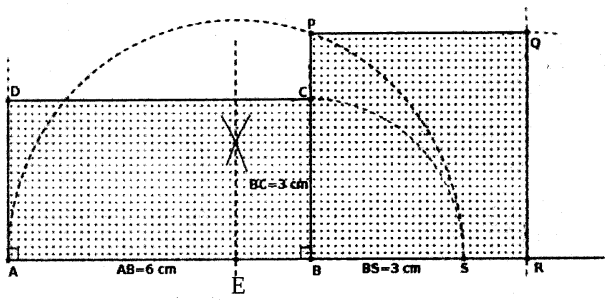
Given area = 18 cm2 So sides be 6 cm and 3 cm.
Construction
Draw a rectangle ABCD length be 5 cm and breadth be 3 cm. To extant the line AB and mark S as BS = 3 cm. Draw a perpendicular bisector of AS and mark E on AS. Draw a semi circle, center be E and radius is AE. BC extant and meet the semi circle at P. Construct a square Sides are BP = PQ = QR = BR. BPQRB be the required square.
Answer 14.
Digits = 1,2,3,4 or 5.
Two digits numbers which will formed by 1, 2, 3, 4 and 5 are 11, 12, 13, 14, 15, 21, 22, 23, 24, 25, 31, 32, 33, 34, 35, 41, 42, 43, 44, 45, 51, 52, 53, 54, 55.
Total number of two digits number = 25, N = 25
a. Both digits being the same = 11, 22, 33, 44, 55, F = 5.
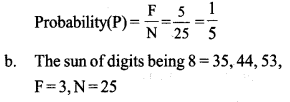

Answer 15.
Given AB = 6 cm, ∠A = 70°, ∠B = 55°
a. ∠C = 180 – (70 + 55) = 180 – 125 = 55°
b. ABC is an isosceles triangle
AB = AC = 6 cm
c. Area of the triangle
![]()
(ADB is right angled triangle. Sin 70 is the included angle of sides AB and AC.)
Area of the triangle
![]()
Answer 16.
Given radius = 13.
Given points = (12, 5), (10, 6). Orgin = (0,0).
Distance b/w (0, 0) and (12, 5)

Answer 17.
Given sides of the triangle (a, b, c) = 30 cm, 28 cm, 26 cm
The perimeter of the triangle
= a + b + c = 30 + 28 + 26 = 84 cm.
Area of the triangle (Using Hero’s formula)

Answer 18.
Given base edge (a) = 10 cm. Height (h)= 12 cm.
a. Slant height (I)
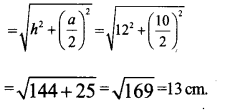
b. Paper needed to make the square pyramid = TSA of the pyramid.
TSA = a2 + 2al
= 102+2 x 10 x 13 = 100 + 260 = 360 cm2
Hence, paper needed to make the square pyramid = 360 cm2
Answer 19.
Given P (x) = ar3 + bx2 + cx + d
P(-1) = -a + b -C + d
Given (x +1) is a factor of P(X).
That means P (- 1) = 0
ie., -a + b – c + d = 0 a + c = b + d.
Hence proved.
P(x) = 6x3 + 4x2 + 3x+5
Answer 20:
a. If joining the mid points of a quadrilateral will give a parallelogram.
The coordinates of R
= (2 x 8 – 4, 4 x 8 – 3) = (6, 9)
b. The coordinates of A = (1, 1).
The coordinates of B
= (2 x 4 – 1,2 x 3 – 1) = (7, 5)
The coordinates of C = (2 x 8 – 7,2 x 8 – 5) = (9, 11)
The coordinates of D
= (2 x 2 – 1,2 x 4 – 1) = (3, 7)
Answer 21.
Consumption | No. of househopds | Consumption (Units) | Cumulative |
| 80 – 100 | 8 | Less than 100 | 8 |
| 100 – 120 | 12 | Less than 120 | 20 |
| 100 – 140 | 10 | Less than 140 | 30 |
| 100 – 160 | 9 | Less than 160 | 39 |
| 100 – 180 | 6 | Less than 180 | 45 |
a. The consumption of 10 houses from 21st to 30th house will be 120 -140 units. The 20 unites between 120 and 140 will have 10 subdivisions and the use of electricity will be the center of each subdivision. The consumption in the 21st house will be 121, between 120 and 122.
b. Median consumption
= 23rd consumption of house.
= 21st consumption of house + 2 x 2 = 121 + 4= 125 Units
Answer 22.
a. The smallest three digit number dividing by 9, the reminder comes up 1 = 99 + 1 = 100
The largest three digit number dividing by 9 = 999 – 8 = 991.
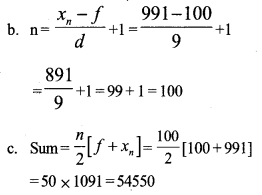
Answer 23.
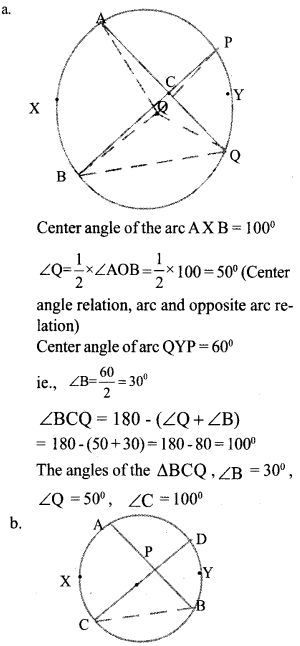
Join C and B.
In ΔPBC , the exterior angle ∠APC = ∠B +∠C(sum of the interior opposite angles)
∠APC = 1/2 [Center angle of the arc AXC + Center angle of the arc BYD]
Hence the ∠APC is the half sum of the center angles of the arc AXC and BYD.
Answer 24.
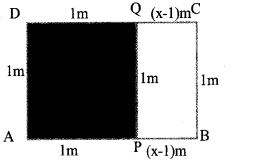
Let the length of the rectangle ABCD be xm
length of the rectangle PBCQ = 1 m Breadth = x – 1m.
b. Given that the ratio of length and breadth of the rectangle ABCD and PBCQ are same.
ie., x: 1 = 1 : x – 1
(The product of means is equal to the product of extreme)
ie., x (x – 1) = 1
x2 – x = 1 x2– x – 1 = 0 is a quadratic equation and find the solution
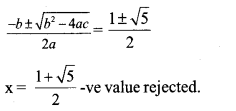
Answer 25.
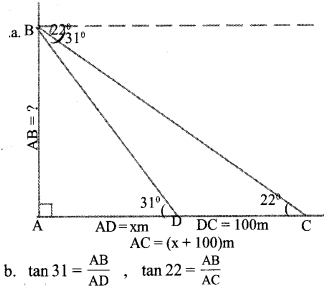

Answer 26.
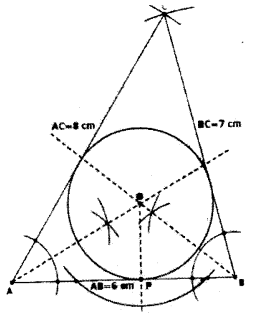
Construct the triangle in the given measurement. Draw any two angle bisector and intersect it at a point O. Draw the circle OP as the radius.
Answer 27.
Given the sector radius = 10 cm and the center angle be 216°.
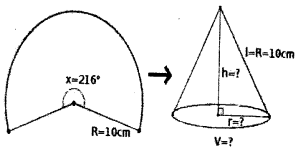
Slant height (1) of the cone = Radius of the sector = 10 cm (given)
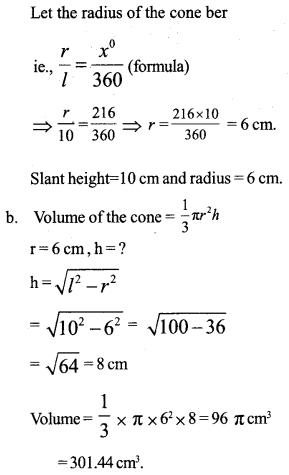
Answer 28.
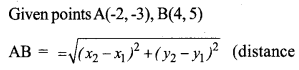

Answer 29.
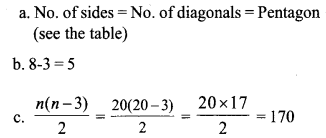
We hope the Kerala SSLC Maths Model Question Papers with Answers Paper 3 help you. If you have any query regarding Kerala SSLC Maths Model Question Papers with Answers Paper 3, drop a comment below and we will get back to you at the earliest.