What is an Equivalent Fraction
Equivalent Fraction
To understand the concept of equivalent fractions, let us take an example – Rama gave four cakes to his four children. The first child cut his cake into two equal halves and ate the first half. The second child cut his cake into four equal parts and ate two pieces out of four. The third child cut his cake into six equal parts and ate three of them, and the fourth child cut the cake into eight equal pieces and ate four of them.
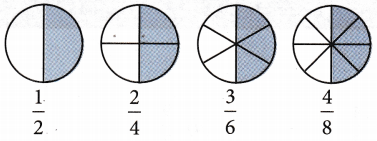
Do you think, they have eaten equal parts of the cake? Yes.
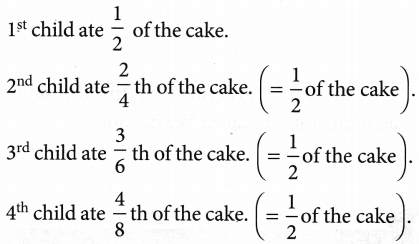
This means they all ate \(\frac{1}{2}\) of the cake. Thus, fractions \(\frac{1}{2}\), \(\frac{2}{4}\), \(\frac{3}{6}\), \(\frac{4}{8}\) represent the same fraction \(\frac{1}{2}\). These are called equivalent fractions. So, two or more fractions representing the same part (value) of the whole are called equivalent fractions.
To check if the fractions are equivalent or not, we do cross-multiplication.
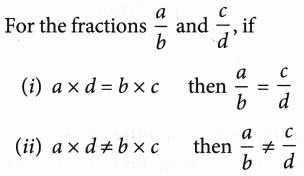

Read More:
- Comparing and Ordering of Fractions
- Conversion of Decimal into Fraction
- Operations on Fractions
- RS Aggarwal Class 6 Solutions Fractions
- RS Aggarwal Class 7 Solutions Fractions
Note:
We can get as many equivalent fractions as we want, by multiplying/dividing the numerator and denominator of the given fraction by the same number.
Example 1: Write five equivalent fractions of \(\frac{3}{5}\)
Solution:
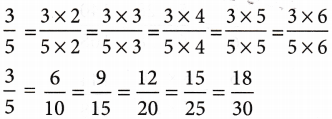
Hence, the five equivalent fractions of \(\frac{3}{5}\) are
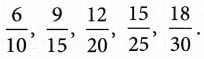
Example 2: Which ofthefollowing pairs of fractions are equivalent:

Solution:
(i) By cross-multiplying the terms of the fractions,
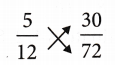
5 × 72 = 12 × 30
360 = 360
∴ \(\frac{5}{12}\) is equivalent to \(\frac{30}{72}\)
(ii) By cross-multiplying the terms of the fractions,
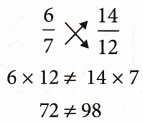
∴ \(\frac{6}{7}\) is equivalent to \(\frac{12}{14}\)
Simplest Form of a Fraction
A fraction is said to be in the lowest term or the simplest form, if its numerator and denominator do not have any common factor other than 1.
Methods to reduce a fraction into the simplest form:
(i) Find the HCF of the numerator and the yg denominator of the given fraction.
(ii) Divide its numerator and denominator by their HCF.
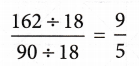
Example: \(\frac{162}{90}\)
HCF of 162 and 90 = 18
Dividing the numerator and denominator of the fraction by their HCF,
So, \(\frac{9}{5}\) is the lowest form of the given fraction because common factor of 9 and 5 is only 1.