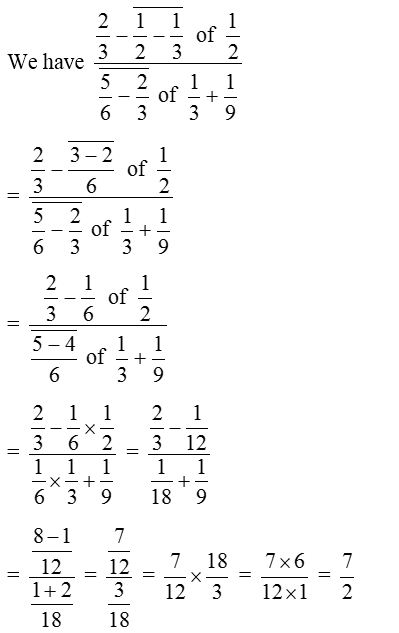What are the Operations on Fractions

What are the Operations on Fractions

Now, we have to learn, how to add and subtract the fractions. Certain methods are to be followed for doing these operations.

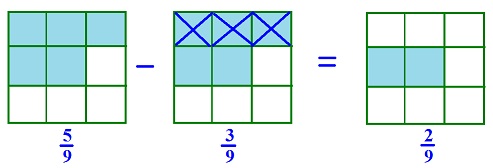
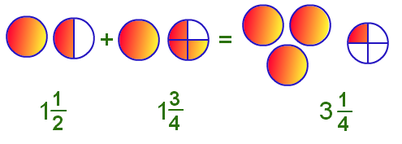
Addition and subtraction of like fractions

For adding and subtracting like fractions, we follow these steps:
Step 1. Add/subtract the numerators with common denominator.
Step 2. Reduce the fraction to its lowest term.
Step 3. If the result is an improper fraction, convert it into a mixed fraction.



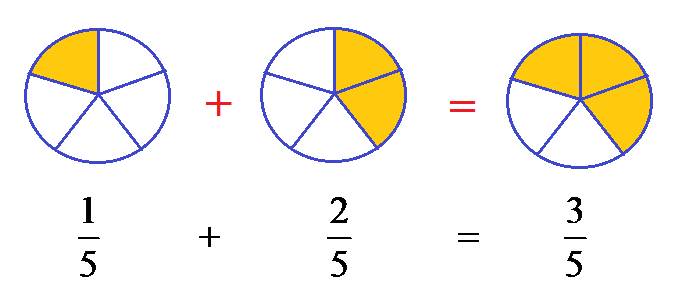
Read More:

• Comparing and Ordering of Fractions
• Conversion of Decimal into Fraction
• RS Aggarwal Class 6 Solutions Fractions
• RS Aggarwal Class 7 Solutions Fractions

Example 1: Find the sum of

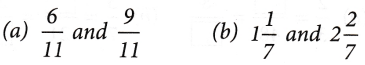
Solution:

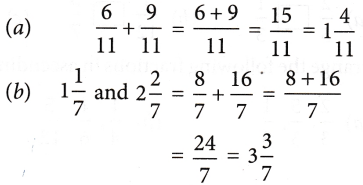
Example 2: Subtract

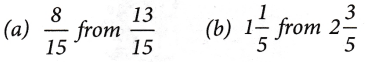
Solution:

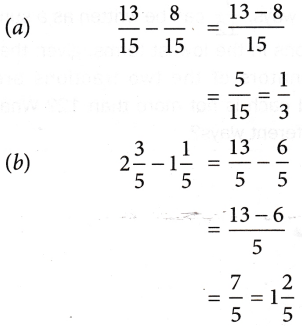
Addition and subtraction of unlike fractions

For adding/subtracting unlike fractions, we follow these steps:
1. Find the LCM of denominators of the given fractions.
2. Convert unlike fractions into like fractions by making LCM as its denominator.
3. Add/ subtract the like fractions.

Example 3: Add \(\frac{9}{5}\) and \(\frac{5}{6}\)
Solution: LCM of 10 and 6 = 30

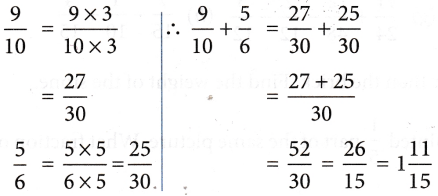
Example 4:

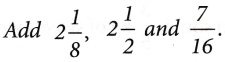
Solution:


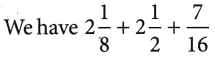
Example 5: Find \(\frac{13}{5}\) – \(\frac{4}{5}\)
Solution: LCM of 15 and 5 = 15

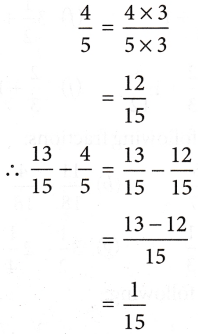
Example 6: Simplify \(6\frac { 1 }{ 2 }\) + \(2\frac{2}{3}\) – \(\frac{1}{4}\)
Solution: \(6\frac { 1 }{ 2 }\) + \(2\frac{2}{3}\) – \(\frac{1}{4}\)

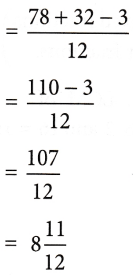
Multiplication of Fractions

Rule:

(i) Whole number by a fraction
(ii) Fraction by a fraction
(iii) Whole number by a mixed fraction
(iv) Multiplication of two mixed fractions

Whole number by a fraction:
To multiply a whole number by a fraction, we simply multiply the numerator of the fraction by the whole number, keeping the denominator same.

Example 1: Find the product

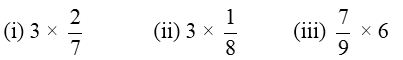
Solution:

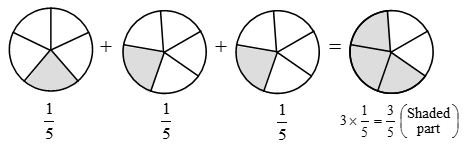
Example 2: Show \(3\times \frac { 1 }{ 5 }\) by picture.
Solution:

Note : Multiplication is commutative i.e. ab = ba

Fraction by a fraction :

Example 3: Find the product

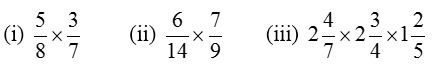
Solution:

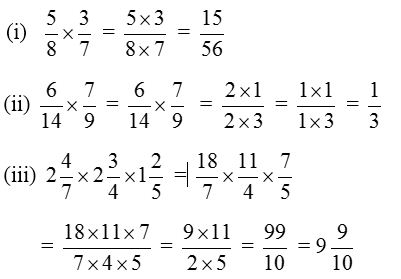
Whole Number by a Mixed Fraction :
To multiply a whole number by a mixed fraction, we follow the following steps:

1. Convert the mixed fraction into an improper fraction.
2. Multiply the numerator by the whole number keeping the denominator same.
3. After multiplication, the fraction should be converted in its lowest form.
4. Convert the improper fraction (product so obtained) into a mixed numeral.

Example 4: Find \(8\times 5\frac { 1 }{ 6 }\)
Solution:

Example 5: Find \(6\times 3\frac { 1 }{ 2 }\)
Solution:

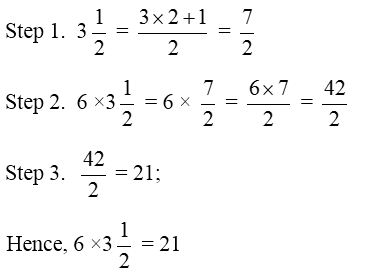
Multiplication of two Mixed Fractions:

1. To multiply two or more mixed numerals, we follow the following steps :
2. Convert the mixed fractions into improper fractions.
3. Multiply the improper fractions.
4. Reduce to lowest form.
5. If the product is an improper fraction, convert it into mixed fraction.

Example 6: Find the product of

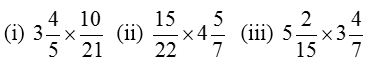
Solution:

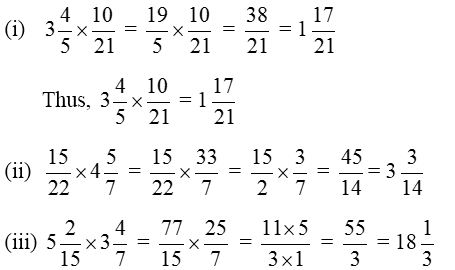
Facts:

1. It is not necessary first to multiply the fractions and then simplify. We may simplify first then multiply. For example,
   
2. Cancellation could use only for fractions are multiplied and could not use for addition & subtraction of fractions.
3. Double of 3 or half of 7 can be written as 2 × 3 and 1/2 × 7 respectively.
   If word ‘OF’ is in between two fractions then multiply those fractions.
4. Product of two proper fractions < Each proper fraction.
   
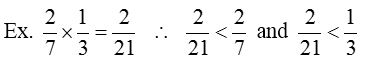
5. Product of two improper fractions > Each improper fraction.
   ;
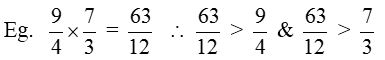6. Proper fraction < Product of proper and improper fraction < Improper fraction
   
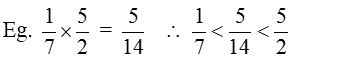
7. When the product of two fractional numbers or a fractional number and a whole number is 1, then either of them is the multiplicative inverse (or reciprocal) of the other. So the reciprocal of a fraction (or a whole number) is obtained by interchanging its numerator and denominator.
   Note : Reciprocal of zero (0) is not possible.

Division of Fractional Numbers

∵ We know Division = Dividend ÷ Divisor
When a fraction number (or whole no.) divide by fractional number (or whole no.) then we multiply dividend to reciprocal of divisor.

Example 1: Find the value of

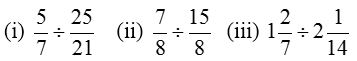
Solution:

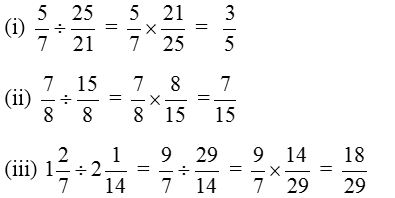
Facts:

1. (Fractional number) ÷ 1 = same fractional number
   
2. 0 ÷ Fractional number = 0 (always)
3. non zero fractional number ÷ same number = 1 (always)
   
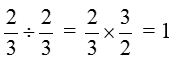
4. ‘0’ cannot be a divisor (∵ reciprocal of zero is not possible)

Example 2:

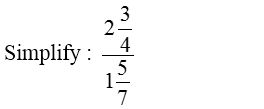
Solution:

Example 3:

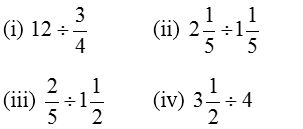
Solution:

Simplifying brackets in fractions

Example 1:

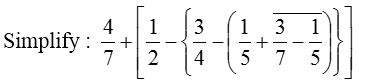
Solution:

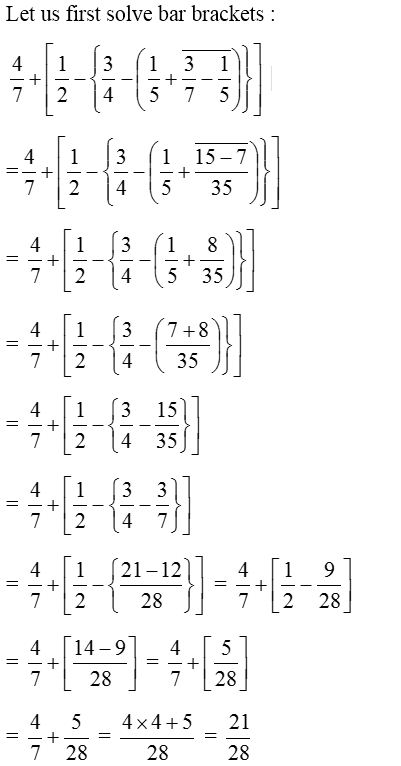
Example 2:

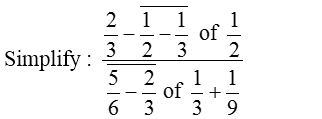
Solution:

Maths