ICSE Solutions for Class 10 Physics – Electricity
ICSE SolutionsSelina ICSE Solutions
APlusTopper.com provides ICSE Solutions for Class 10 Physics Chapter 7 Electricity for ICSE Board Examinations. We provide step by step Solutions for ICSE Physics Class 10 Solutions Pdf. You can download the Class 10 Physics ICSE Textbook Solutions with Free PDF download option.
Download Formulae Handbook For ICSE Class 9 and 10
Short Answers
Question 1: State and define Ohm’s law.
Answer: Ohm’s law states that at a constant temperature, the current flowing in a conductor is directly proportional to the potential difference across its ends, i.e., if the potential difference is halved, the current is also halved and if p.d. is doubled, the current is also doubled, i.e.,
V (potential difference) ∝ i (current)
Or V = iR, where R is constant, called the resistance of the conductor.
So V = iR represents Ohm’s law.
Question 2: Define the unit ohm.
Answer: One ohm is the resistance of a conductor in which 1 ampere current flows when the potential difference across its ends is 1 volt.
Question 3: Define ampere and volt with respect to Ohm’s law.
Answer: Ampere: It is the S.I. unit of current. If a current flows in a conductor of resistance of 1Ω, when the potential difference across its ends is 1 volt, the current is said to be 1 ampere, i.e.,
1 ampere = 1 volt/1 ohm
Volt: It is the S. I. unit of potential difference. If a current of 1 ampere flows in a conductor of resistance 1 ohm, then potential difference across its ends is said to be 1 volt, i.e.,
1 volt = 1 ampere × 1 ohm.
Question 4: State the limitations of Ohm’s law.
Answer: There are two main limitations:
(i) Temperature, (ii) Physical condition of the conductor.
It is found that the ratio V/I is mo longer constant when the temperature is not kept constant. Generally, resistance increases with the rise in the temperature of the conductor.
Physical conditions of any conductor mainly include:
(i) Its length, (ii) Its cross-sectional area, (iii) The kind of the material.
If there is no change in any of the above three conditions and also other condition like temperature remains constant, then Ohm’s law holds good, i.e., the ratio V/I remains constant.
Question 5: What is non-ohmic resistor?
Answer: This is a resistor which does not obey Ohm’s Laws.
V -1 graph for non-ohmic resistor is not a straight line.
Question 6: Define the term potential and state its S.I. unit.
Answer: Potential at a point is defined as the work done in bringing a unit positive charge from infinity
to that point. Its S.I. unit is volt, where 1 V = 1 joule/1 coulomb
Question 7: Explain, why the potential difference across the terminals of a cell is more when the cell is not in use than it is when the cell is being used.
Answer: The reason is that when the cell is being used, there is a drop in potential across the internal resistance of the cell.
Question 8: What is e.m.f. of a cell? A cell is sending current in an external circuit. How does the terminal voltage compare with the e.m.f. of the cell?
Answer: When no current is drawn from a cell, i.e., when the cell is not connected to any external circuit (or is in open circuit), then the potential difference between its electrodes (or plates) is called its electromotive force, i.e., e.m.f. It is denoted by E. Emf of a cell is greater than terminal voltage.
Question 9: State the factors on which the e.m.f of a cell depends.
Answer: The e.m.f. of different cell depends on the following factors:
(i) The material of the electrodes. (ii) The electrolyte used in the cell.
It is to be noted that the e.m.f. of a cell does not depend on its shape or size.
Question 10: A cell of e.m.f. E and internal resistance r is used to send current I in an external resistance R. Write expressions for (i) the current drawn from the cell, (ii) the terminal voltage V of the cell, and (iii) the voltage drop across the internal resistance. How are E and V related?
Answer: Total resistance of circuit = R + r
![]()
(ii) The terminal voltage of the cell, V = IR
(iii) The voltage drop across the internal resistance = IR
E and V are related as E = V + IR.
Question 11: Point out two differences between e.m.f. and potential difference as applied to electric circuits.
Answer: Electromotive force or e.m.f. of a cell is potential difference between its two electrodes when it is in open circuit, i.e., not sending current in the external circuit; while potential difference is the difference in potential between the terminals when the cell is in closed circuit or it is sending current in the given circuits, e.m.f. is always greater than potential difference or terminal voltage of a cell on account of energy being spent in driving charge through the circuit.
Question 12: Explain why potential difference is always less than the e.m.f. of a cell?
Answer: When a cell is in closed circuit, i.e., when current is drawn from it, then the potential difference between its electrodes is called the terminal voltage. It is always less than the e.m.f. because when charge flows in a circuit, some energy is spent in the flow of charge through the electrolyte of the cell.
Question 13: Define the term current and state its S.I. unit.
Answer: Current is defined as the amount of charge flowing per second.

Question 14: What is the voltage of the electricity that is generally supplied to a house?
Answer: The voltage of the electricity which is generally supplied to a house is 220 volt at 50 Hz.
Question 15: How is direction of current related to the direction of flow of electrons?
Answer: The direction of current is opposite to the direction of flow of electrons.
Question 16: Write an expression for the electrical energy spent in the flow of current through an electrical appliances in terms of I, R and t.
Answer: Electric energy = I2Rt.
Question 17: What do you understand by the resistance of a wire?
Answer: The obstruction offered in the flow of electrons (or current) by the material of the wire, is called its resistance.
Question 18: State the S.I. unit of electrical resistance and define it.
Answer: The S.I. unit of electrical resistance is ohm (Ω). The resistance of a conductor is said to be 1 ohm if 1 ampere current flows through it when the potential difference across its end is 1 volt.
Question 19: State four factors on which resistance of a conductor depends.
Answer: (i) Length of conductor. (ii) Area of cross-section of conductor.
(iii) Material of conductor. (iv) Temperature of conductor.
Question 20: How does the resistance of a metallic wire depend on the following:
(i) the length of wire; (ii) the thickness of wire, (iii) the temperature of wire?
Answer: (i) The resistance of a wire increases with increases in the length of wire (R ∝ l).
(ii) The resistance of a wire decreases with increase in its thickness (R ∝ l/a where a = πr2, the area of cross-section of the wire).
(iii) The resistance of a metallic wire increases with increase in its temperature.
Question 21: A given wire is stretched to double its length. How will its resistance change?
Answer: When a given wire is stretched to double its length, its area of cross-section will be halved, so the resistance of wire will become four times.
Question 22: A given metallic wire of resistance R is doubled on itself. What will be its new resistance?
Answer: When a given metallic wire is doubled on itself, its length is reduced to half, but its area of cross-section gets doubled. So, the resistance of the wire will become one-fourth i.e., the new resistance of wire will be R/4 (or 0.25 R).
Question 23: How does the resistance of (i) a semi-conductor, and (ii) an alloy, vary with temperature?
Answer: (i) The resistance of a semi conductor decreases with increase in temperature.
(ii) The resistance of an alloy remains nearly unaffected by the change in temperatue.
Question 24: Bends in a rubber pipe reduce the flow of water through it. How would the bands in a wire affect its electric resistance?
Answer: Bends in the wire will not affect its resistance. This is because the electrons are extremely small in size as compared to the bends. So, the electrons can easily change their direction of motion.
Question 25: State the order of resistivity of (i) a metal, (ii) a semi-conductor, and (iii) an insulator.
Answer: (i) 10-8 ohm × m (ii) 10-3 ohm × m (iii) 1010 ohm × m.
Question 26: Name the material of wire used for making standard resistances. Give a reason.
Answer: Constantan is used for making standard resistances. The reason is that its resistance remains almost unaffected with change in temperature.
Question 27: What material is used for making wire to prepare heating coils? Give a reason.
Answer: Nichrome is used for making wire to prepare heating coils. The reason is that its melting point is high and its resistivity is also high.
Question 28: Why are thick copper wires used as connecting wires?
Answer: The resistance of connecting wires should be almost negligible. For this thick wires are used . since a thicker wire has a small resistance and the wires are made of copper because the resistivity of copper is low.
Question 29: State the effect of rise in temperature on the resistance of semi-conductors.
Answer: In the case of semi-conductors like carbon, silicon, germanium, etc., the resistance decreases with increase in temperature.
Question 30: Write an expression for the resistance of a conducting wire in terms of its length and area of cross-section.
Answer: Let R be the resistance of a conducting wire of length l and area of cross-section A. We then have:
R = ρl/A
Here ρ is a constant characteristic of the material of the wire and is called its resistivity. Thus,
![]()
Question 31: How does the resistivity of a metallic wire depend on temperature?
Answer: The resistivity of a metallic wire increases with increase in temperature.
Question 32: How does the resistivity of a semiconductor depends on temperature.
Answer: The resistivity of a semi conductor decreases with increase in temperature.
Question 33: How does the resistivity of an alloy such as constantace depends on temperature.
Answer: The resistivity of an alloy almost remains unaffected with change in tempeature.
Question 34: State expression for Cells connected in series.
Answer:
![]()
Question 35: What is meant by internal resistance of a cell?
Answer: The resistance offered by the electrolyte inside the cell to the flow of current is called internal resistance of cell.
Question 36: Define the term resistivity and state its S.I. unit. Which will have higher resistivity a conductor or an insulator.
Answer: The resistivity of a substance is the resistance of a wire of that substance of unit length and unit area of cross-section. Its S. I. unit is ohm × m. An insulator will have higher resistivity.
Question 37: The voltage applied to a given rheostat is made four times its initial value. By what factor will be resistance of the rheostat change?
Answer: The resistance of the rheostat will not change at all as it does not depend on the voltage applied across it.
Question 38: Two copper wires are of the same length, but one is thicker than the other.
(i) Which wire will have more resistance?
(ii) Which wire will have more specific resistance?
Answer: (i) Thinner wire will have more resistance. R ∝ l/a area of cross-section.
(ii) Thicker wire will have more specific resistance. Since specific resistance is directly proportional to length.
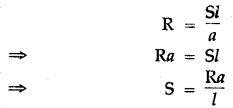
Question 39: State expression for Resistance connected in series.
Answer: R = r1 + r2 + r3, resistances in series.
Question 40: State expression for Resistance connected in parallel.
Answer:
![]()
Question 41: State expression for Cells connected in parallel.
Answer:
![]()
Question 42: State the condition when it is advantageous to connect cells—(i) in series, and (ii) parallel.
Answer: (i) It is advantageous to connect cells in series if the external resistance is large enough compared to the total internal resistance of cells.
(ii) It is advantageous to connect cells in parallel if the internal resistance of each cell is high enough compared to the external resistance.
Question 43: State the factors on which the internal resistance of a cell depends.
Answer: The factors which govern the internal resistance of cell are:
(i) The surface area of the electrodes: The larger the surface area, less is the internal resistance.
(ii) The distance between the electrodes: As the distance between the electrodes increases, the internal resistance of cell also increases. It is also affected by the nature, concentration and temperature of the solution (electrolyte).
Question 44: How should the electric lamps in a building be connected?
Answer: Electric lamps are connected in parallel.
Question 45: What determines the direction of flow of electrons between two charged conductors kept in contact?
Answer: The potentials of the two conductors determine the direction of flow of electrons. The electrons flow from the conductor at low potential to the conductor at high potential.
Question 46: What is consumed using different electrical appliances, for which electricity bills are paid?
Answer: Electrical energy in kWh which is commercially called a unit of electrical energy.
1 kWh = 1 kW × 1 hr = 1 unit of electricity.
Question 47: Write an expression for calculating electrical power in terms of current and resistance.
Answer: Electrical power in terms of current and resistance is P = I2R.
Question 48: Give two differences between a d.c. motor and an a.c. generator.
Answer: Two differences between d.c. motor and a.c. generator are given below:
| D.C. Motor | A .C. Generator |
| 1. It is a device which converts electrical energy into mechanical energy. | It is a device which converts mechanical energy into electrical energy. |
| 2. It works on the principle of magnetic effect of current. | It works on the principle of electromagnetic induction. |
Question 49: Which part of an electrical appliance is earthed?
Answer: Metal body of an electrical appliance is earthed.
Question 50: State the conditions for the flow of charge in a circuit from one point to the other.
Answer: The main condition for the flow of charge between two points is the difference in their potentials. If the potential difference is greater, a strong current flows and if both points are at the same potential, no current will flow.
Question 51: An electrical gadget can give an electric shock to its user under certain circumstances. Mention any two of these circumstances.
Answer: When the live wire comes in contact with the metal body of the electrical gadget.
Question 52: What is the purpose of using a fuse in an electrical circuit?
Answer: Fuse is a safety device which is used to limit the current in an electric circuit.
Question 53: What are the characteristic properties of fuse wire?
Answer: Characteristic properties of a fuse wire:
(i) It is made up of an alloy of lead and tin.
(ii) It has high resistivity and low melting point.
Question 54: A substance has nearly zero resistance at a temperature of 1 K. What is such a substance called?
Answer: Super conductor.
Question 55: What is an Ohmic resistor?
Answer: An ohmic resistor is a resistor which obeys ohm’s law i.e., its resistance remains constant with increase in temperature
V ∝ I
V = IR at constant temperature.
Question 56: What is the colour code for the insulation on the earth wire?
Answer: Earth wire – Insulation is of Green or Yellow colour.
Question 57: State a relation between electrical power, resistance and potential difference in an electrical circuit.
Answer: In an electrical circuit, electrical power
P = V2/R
where V = potential difference and R = resistance.
Long Answers
Question 1: What is a resistance? Define it with respect to Ohm’s law,
Answer: In the flow of current in a conductor, electrons are drifted. During this drift or flow, electrons mutually collide against each other and the atoms of the conductor. These collison give rise to some obstruction to the flow of electrons. This opposition or obstruction offered by a conductor to the flow of electrons is called ‘Resistance’. According to Ohm’s law, the ratio between potential difference V and the current i, is a constant provided the temperature and physical conditions of the conductor remain unaltered. As such the ratio V/I is called the resistance, i.e., ‘Ohmic resistance’ of the conductor.
Question 2: State and explain the laws of resistance.
Answer: The following are the main laws of resistance:
(i) Resistance of a conductor is directly proportional to its length, provided temperature and other physical conditions remain unchanged.
It means that R ∝ l i.e., if the length increases, the resistance also increases and if length decreases, its resistance also decreases.
(ii) Resistance of a conductor is inversely proportional to its area of cross section, other conditions remaining the same.
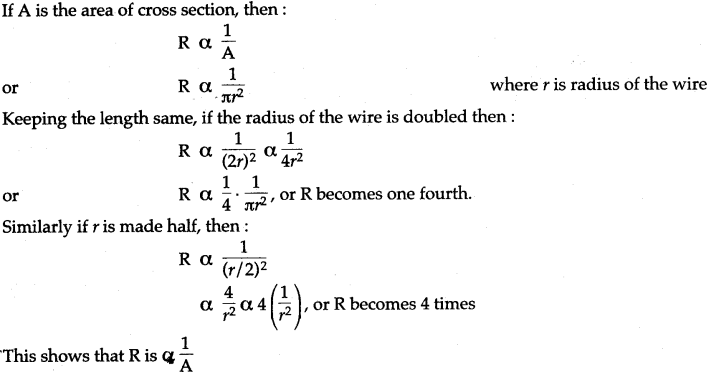
(iii) R depends on the nature of the material of the conductor. It means, if we take equal lengths of wires of copper, aluminium and iron and all of the same cross-sectional area, their resistance are different from each other since they are of different materials.
Figure Based Short Answers</span
Question 1: What are ohmic conductors? Give one exmaple. Draw a graph showing the current-voltage relationship for an ohmic conductor.
Solution: The conductors which obey Ohm’s law (i.e., V/I is constant) are called ohmic conductors.
Example: Silver.
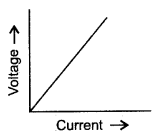
A graph showing the current-voltage relationship for a ohmic conductor is shown in the figure.
Question 2: What are non-ohmic conductors? Give one exmaple. Draw a current-voltage graph for a non-ohmic conductor.
Solution:The conductors which do not obey Ohm’s law (i.e., V/I is not constant) are called non-ohmic conductors.
Example: Diode valve.
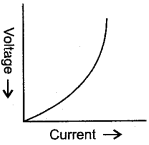
The current-voltage graph for a non-ohmic conductor is shown in figure alongside.
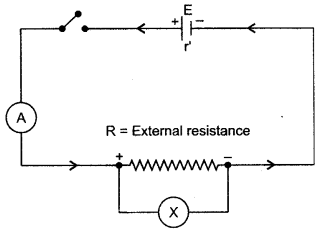
Question 3: Draw a neat diagram for the verification of Ohm’s law by voltmeter-ammeter method. By another diagram show the relation between p.d. and current.
Solution:
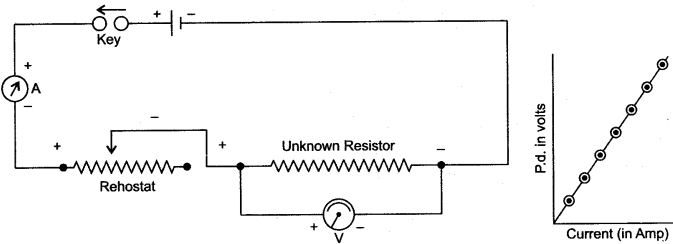
Question 4: A cell of emf. 1.5 V and internal resistance 10 ohms is connected to a resistor of 5 ohms, with an ammeter in series (see fig.). What is the reading of the ammeter?
Solution:
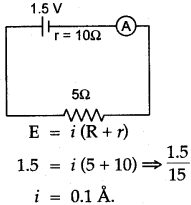
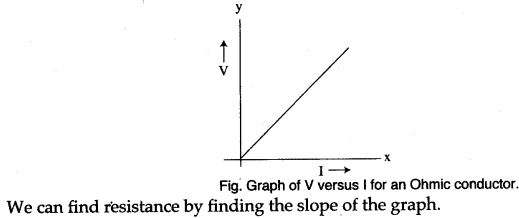
Question 5: Draw a graph of Potential difference (V) versus Current (I) for an ohmic resistor. How can you find the resistance of the resistor from this graph?
Answer: We can find resistance by finding the slope of the graph.
Question 6: The V-I graph for a series combination and of a parallel combination of two resistors is as shown in the figure:
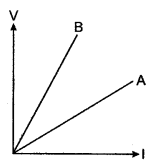
Which of the two, A or B, represents the parallel combination? Give a reason for your answer.
Answer: ‘A’ shows parallel combination because in case of parallel combination, the resistance is less for their potential is less, currents is more.
Question 7: In given figure, calculate the effective resistance between the points A and B.
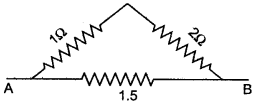
Solution:
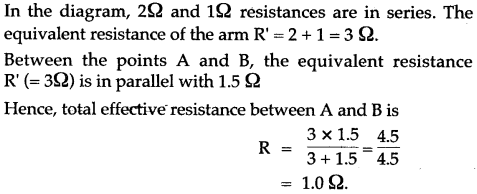
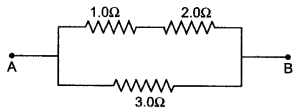
Question 8: You are provided with three resistors of resistance 1.0 Ω, 2.0 Ω and 3.0 Ω How would you connect them to obtain the total effective resistance 1.5 Ω? Draw diagram of the arrangement and check it by calculations.
Solution:
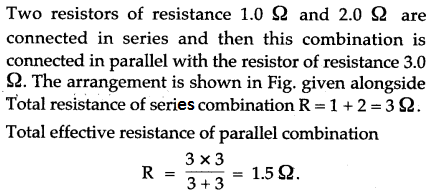
Question 9: Three resistors, each of 2Ω are connected together so that their total resistance is 3Ω Draw a diagram to show this arrangement and check it by calculations.
Solution:
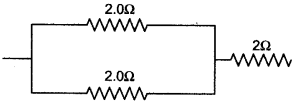

Then total resistance of series combinations of R’ = 1Ω with 2Ω resistors is R = 1 + 2 = 3Ω.
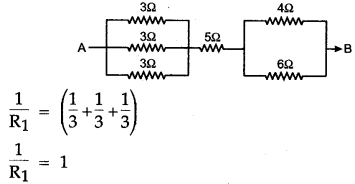
Question 10: Find the equivalent resistance between points A and B.
Solution:
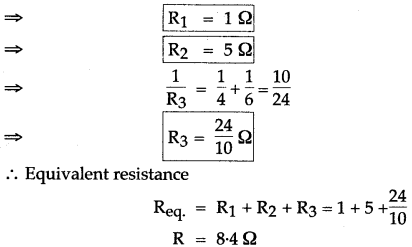
Question 11: Calculate the equivalent resistance between the points A and B for the following combination of resistors:
Solution:
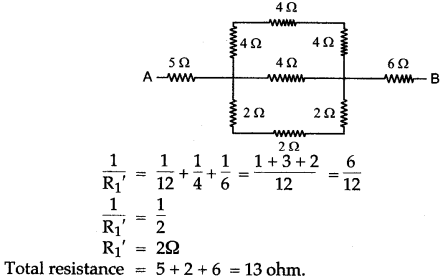
Question 12: Calculate the equivalent resistance between P and Q from the following diagram:
Solution:
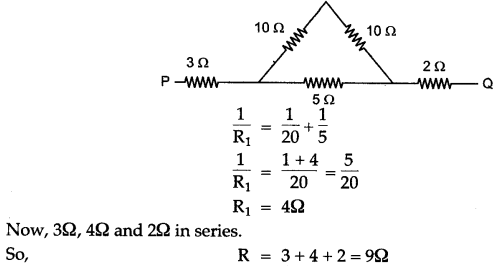
Question 13: Calculate the equivalent resistance between A and B from the following diagram:
Solution:
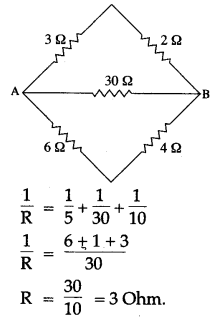
Question 14: Six resistances are connected together as shown in the figure. Calculate the equivalent resistance between the points A and B.
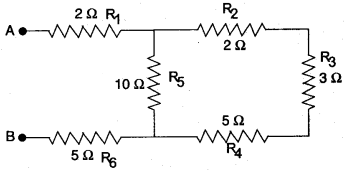
Solution:
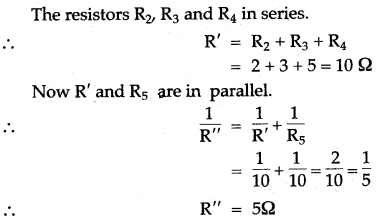
Now R1, R” and R6 in series between the points A and B. The equivalent resistance between A and B is
R = R1 + R” + R6 = 2 + 5 + 5 = 12Ω
Question 15: Four resistances of 2.0Ω each are joined end to end, to form a square ABCD. Calculate the equivalent resistance of the combination between any two adjacent comers.
Solution: The diagram indicates a square ABCD formed by joining four resistances of 2Ω each, end to end.
Let us calculate the equivalent resistance of the combination B between the two adjacent comets C and D.


Question 16: Three resistors of 6Ω, 3Ω and 2Ω are connected together so that their total resistance is greater than 6Ω but less than 8Ω Draw a diagram to show this arrangement and calculate its total resistance.
Solution:

Question 17: In the circuit shown below, calculate the equivalent resistance between the points (i) A and B, (ii) C and D.
Solution:
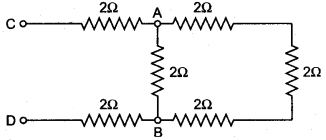

(ii) Between the points C and D:
The above combination of equivalent resistance 1.5 Ω is in series with two resistances 2Ω and 2Ω
Total effective resistance between the points C and D is R = 1.5 + 2 + 2 = 5.5
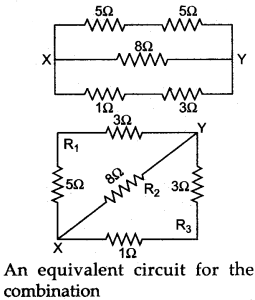
Question 18: What is the equivalent resistance between the points X and Y for the given network?
Solution:
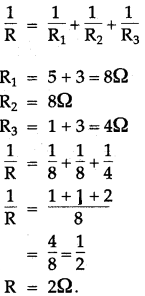
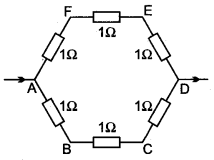
Question 19: Six equal resistors of 1 ohm each are connected to form the sides of a hexagon ABCDEF. Calculate the resistance offered by the combination if the current enters at A and leaves it at D.
Solution: From figure it is clear that there are two sets of parallel resistances between A and D. Each group has three resistances of 1Ω each, in series. Equivalent resistance R1 of one group (AB, BC and CD) = 1Ω + 1Ω + 1Ω = 3Ω
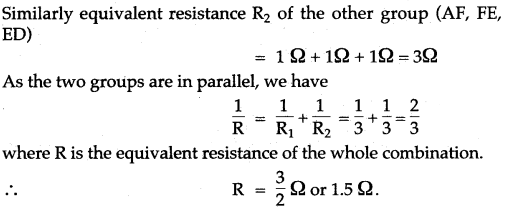
Question 20: Two lamps of resistance 30Ω and 20Ω respectively are connected in series in a 110V circuit. Calculate (i) the total resistance in the circuit (ii) the current in the circuit, and
(iii) the voltage drop across each lamp.
Solution:


Question 21: Calculate the equivalent resistance of the following combinations of resistors r1, r2, r3, r4.
Solution:

Question 22: Four cells, each of e.m.f. 1.5 V and internal resistance 2.0 ohms are connected in parallel. The battery of cells is connected to an external resistance of 2.5 ohms. Calculate:
(i) The total resistance of the circuit.
(ii) The current flowing in the external circuit.
(iii) The drop in potential across-the terminals of the cells.
Solution: E.m.f. of cell (each) = 1.5 V. and also e.m.f. of all four cells = 1.5V, internal resistance of each cell = 2.0 ohm.
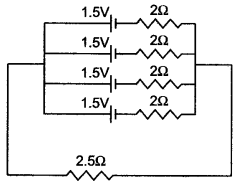
Total internal resistance of all four cells

Question 23: 2Ω resistor A, 1Ω resistor B and 4Ω resistor C are connected in parallel. The combination is connected across a 2V battery of negligible resistance. Draw the diagram of the arrangement and calculate: (i) The current in each resistor A and C, (ii) The current through battery.
Solution: The diagram of the arrangement is shown in Fig.
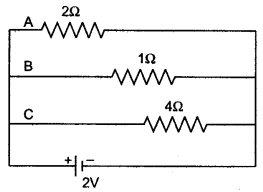
![]()

Figure Based Long Answers
Question 1: Define the e.m.f. (E) of a cell and the potential difference (V) of a resistor R in terms of the work done in moving a unit charge. State the relation between these two works and the work done in moving a unit charge through a cell connected across the resistor. Take the internal resistance of the cell as ‘r’. Hence obtain an expression for the current i in the circuit.
Answer: E. M. F. of a cell is generally defined as the amount of work done (or the energy spent) in taking a unit positive charge around the complete circuit of the cell (i.e., in the wire outside the cell and the electrolyte within the cell). It is also defined as the potential difference between the terminals of a cell when no current is drawn from it (or when the cell is in open circuit).
Potential difference (p.d.) or the terminal voltage of a cell is generally defined as the amount of work done in carrying a unit positive charge round the circuit connected across the terminals of the cell. If W is the amount of work done (in J) in moving a test charge q between the terminals of a cell through a resistor R, then the p.d. i.e., work done in moving a unit positive charge across the terminals of the cell.
Relation between E, V (p.d.), external resistance R and the internal resistance r’,

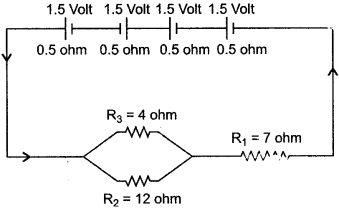
Question 2: A battery of 4 cell, each of e.m.f. 1.5 volt and internal resistance 0.5 Ω is connected to three resistances as shown in the figure. Calculate:
(i) The total resistance of the circuit.
(ii) The current through the cell.
(iii) The current through each resistance.
(iv) The p.d. across each resistance.
Solution: Let total e.m.f. of 4 cells = nE (n = number of cells)
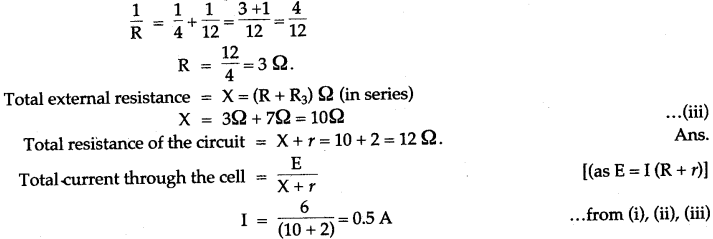

Question 3: Four cells each of e.m.f. 2V and internal resistance 0.1 Ω are connected in series to an ammeter of negligible resistance, a 1.6 Ω resistor and an unknown resistor R1. The current in the circuit is 2A. Draw a labelled diagram and calculate:
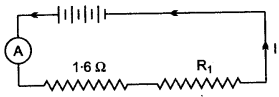
(i) Total resistance of the circuit, (ii) Total e.m.f. (iii) The value of R1 and (iv) The p.d. across R1.
Solution:
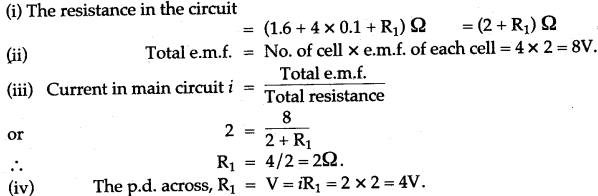
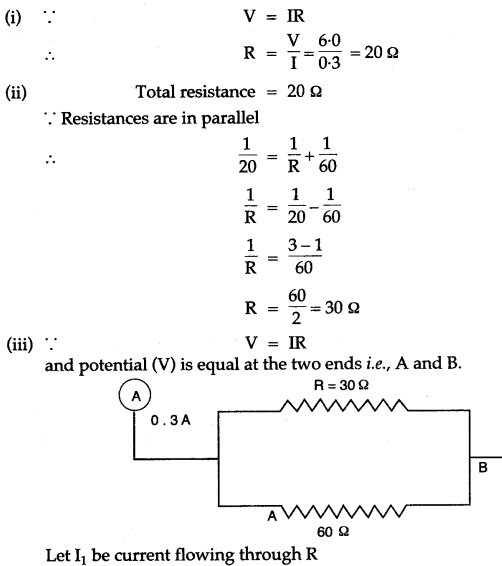
Question 4: In the figure below, the ammeter A reads 0.3 A. Calculate:
(i) the total resistance of the circuit (ii) the value of R
(iii) the current flowing through R.
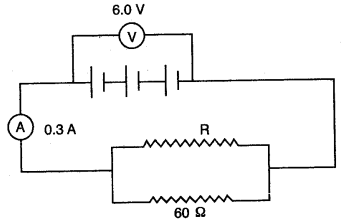
Solution:

Question 5: Three resistors are connected to a 12 V battery as shown in the figure given below:
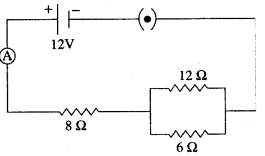
(i) What is the current through the 8 ohm resistor?
(ii) What is the potential difference across the parallel combination of 6 ohm and 12 ohm resistor?
(iii) What is the current through the 6 ohm resistor?
Solution: (i) 6 ohm and 12 ohm are connected in parallel, So

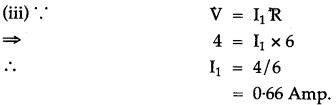
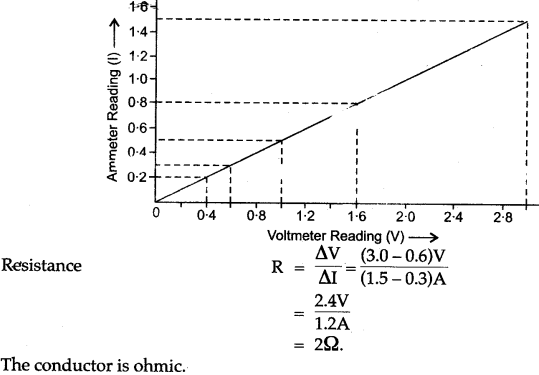
Question 6: From the following observations taken while determining the resistance of a conductor, draw the current-voltage graph and calculate the resistance of conductor. Is the conductor ohmic?
| Ammeter reading I (in ampere) | Voltmeter reading V (in volt) |
| 0.2 | 0.4 |
| 0.3 | 0.6 |
| 0.5 | 1.0 |
| 0.8 | 1.6 |
| 1.5 | 3.0 |
Solution: The current voltage graph is shown in figure.
Question 7: Calculate equivalent resistance in the following cases:
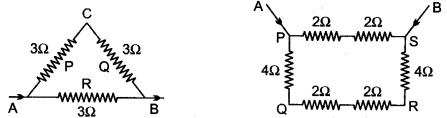
Solution:

Question 8: Three resistors are connected to a 6 V battery as shown in the figure given below:
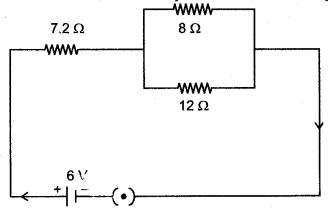
Calculate:
(i) the equivalent resistance of the circuit.
(ii) total current in the circuit.
(iii) potential difference across the 7.2 Ω resistor.
Solution:

Question 9: Five resistors of different resistances are connected together as shown in the figure. A 12 V battery is connected to the arrangement.
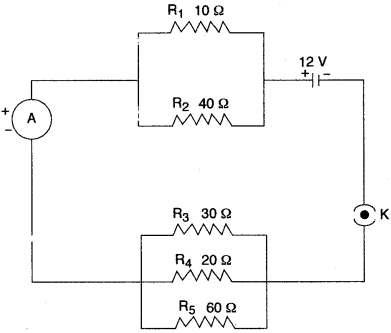
Calculate:
(i) the total resistance in the circuit
(ii) the total current flowing in the circuit.
Solution:

Question 10: Suppose there are three resistors A, B and C having resistances r1, r2 and r3 respectively. If R represent their equivalent resistance, establish the following relations:
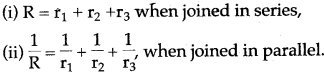
Solution:
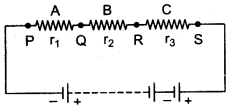
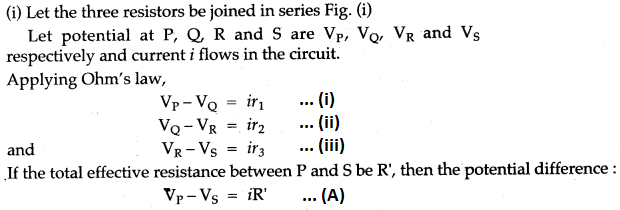


Question 11: Illustrate-combination of cells e.g., three cells, in (i) series and (ii) parallel, explaining each combination briefly. Obtain an expression for current ‘i’ in each combination.
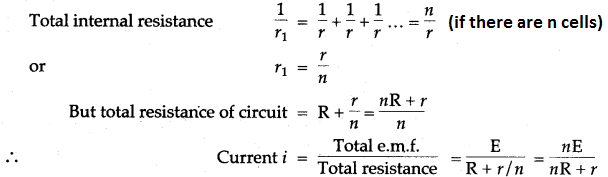
Solution: (i) Combination of cells in series:

In this combination, the cells are so connected that the negative terminal of one cell is connected to the positive terminal of the other cell such that in the end one free positive and one free negative terminal are left. These free terminals are connected to the external circuit. If the e.m.f of each cell is E and Y be the internal resistance and I be the current, then e.m.f. of the cell in series = nE (here n = 3)
The total internal resistance = nr
and External resistance = R
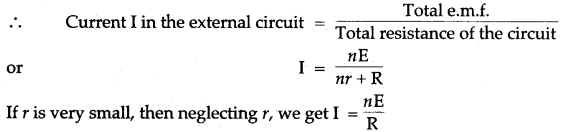
This shows that it is advantageous to connect cells in series to get a large current when their internal resistance is negligible.
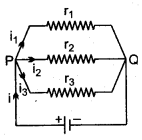
(ii) Combination of cells in parallel: Let there be n cells, each of e.m.f. E and internal resistance r, be connected in parallel as shown in the diagram.
Total e.m.f. across the point A and B is E
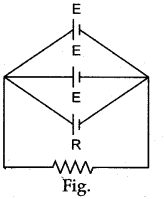
It is advantageous to join cells in parallel when the internal resistance of each cell is quite high as compared to the external resistance R.
![]()
Question 12: Two resistors of 4Ω and 6Ω are connected in parallel to a cell to draw 0.5 A current from the cell.
(i) Draw a labelled circuit diagram showing the above arrangement.
(ii) Calculate the current in each resistor.
Solution: (i)
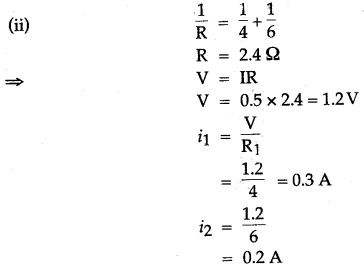
Question 13: The figure shows a circuit.
When the circuit is switched on, the ammeter reads 0.5 A.
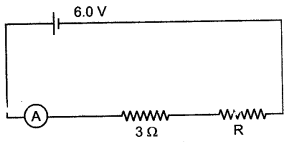
(i) Calculate the value of the unknown resistor R.
(ii) Calculate the charge passing through the 3 Ω resistor in 120 s.
(iii) Calculate the power dissipated in the 3 Ω resistor.
Solution:

Question 14: In the figure given below, A, B and C are three ammeters. The ammeter B reads 0.5A. (All the ammeters have negligible resistance.)

Calculate:
(i) the readings in the ammeters A and C.
(ii) the total resistance of the circuit.
Solution:

∴ Current through A = Current passing through B + current passing through C
= 0.5 + 1.0 = 1.5 ampere
Short Numericals
Question 1: A cell supplies a current of 0.6 A through a 2Ω coil and a current of 0.3 A through on 8Ω coil. Calculate the e.m.f and internal resistnce of the cell.
Solution:
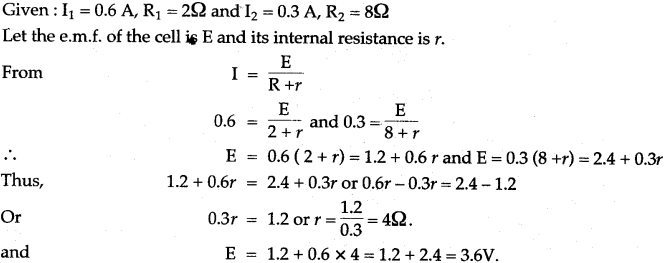
Question 2: A cell of e.m.f 2.0 V and internal resistance 1Ω is connected to the resistors of 3Ω and 6Ω in series. Calculate: (i) the current drawn from the cell, (ii) the p.d. across each resistor, (iii) the terminal voltage of the cell and (iv) the voltage drop.
Solution:

Question 3: A current of 0.2 A flows through a conducting wire for 5 minutes. How much charge will flow?
Solution: Given: I = 0.2A, t = 5 minute = 5 × 60s = 300s.
Charge Q = I × t = 0.2 × 300 = 60 C.
Question 4: A current of 100 mA. flows through a wire. The charge on an electron is 1.6 × 10-19 C. Find the number of electrons passing per second through the cross-section of the conductor.
Solution: Given: I = 100mA = 100 × 10-3 A = 0.1A, e = 1.6 × 10-19 C
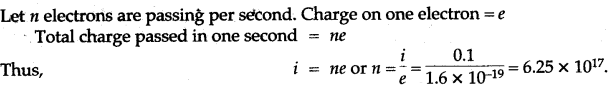
Question 5: An electric bulb draws 0.5 A current at 3.0 V. Calculate the resistance of the filament of the bulb.
Solution:

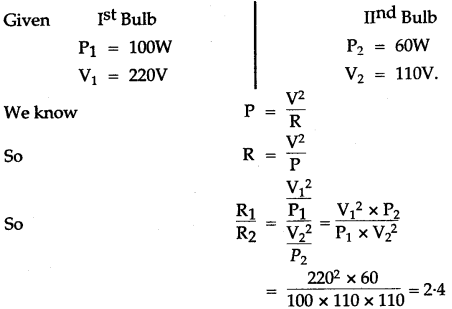
Question 6: Two bulbs are marked 100 W, 220 V and 60 W, 110 V. Calculate the ratio of their resistances.
Solution:
Question 7: An ammeter placed in series with an electric radiator reads 0.5 amps and a voltmeter placed across it reads 230 volts. What is the resistance of the radiator?
Solution:
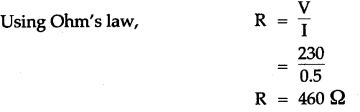
Question 8: What should be the length of a nickel wire of area of cross-section 3 mm2 used for making a rheostat of 750 ohm? (ρ of nickle = 0.069 Ohm mm2/m)
Solution:

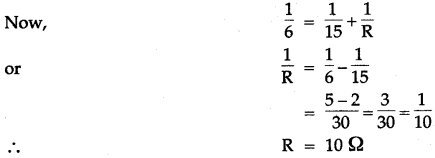
Question 9: Calculate the value of the resistance which must be connected to a 15 ohm resistance to provide on effective resistance of 6 ohm.
Solution: Resistance decreases in parallel combination. S let R resistance is connected to 15 Ω resistance parallel to make resultant 6 ohm.
Question 10: A metal wire of resistance 6 Ω is stretched so that its length is increased to twice its original length. Calculate its new resistance.
Solution:
R’ = n2R
= 22 × 6 = 24 Ohm.
Question 11: Calculate the quantity of heat that will be produced in a coil of resistance 75 Ω if a current of 2A is passed through it for 2 minutes.
Solution:
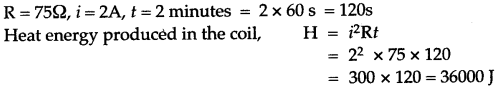
Question 12: Two wires of same material and same lengths have radii in the ratio of 2 : 3, Compare their resistances.
Solution:
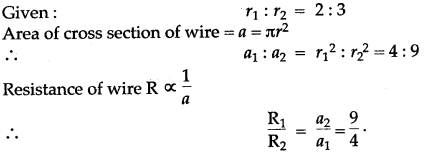
Question 13: Two resistors having 2Ω and 3Ω resistance are connected—(i) in series, and (ii) in parallel. Find the equivalent resistance in each case.
Solution:

Question 14: A wire of uniform thickness with a resistance of 27Ω is cut into three equal pieces and they are joined in parallel. Find the resistance of the parallel combination.
Solution:

Question 15: The resistance of two resistors joined in series is 8Ω and in parallel is 1.5Ω. Find the value of the two resistances.
Solution:
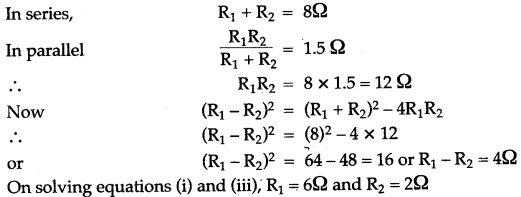
Question 16: An electrical appliance is rated at 1000 KVA, 220V. If the appliance is operated for 2 hours, calculate the energy consumed by the appliance in: (i) kWh (ii) joule.
Solution:

Question 17: An electric bulb is marked 100 W, 250 V. What information does this convey? How much current will the bulb draw if connected to a 250 V supply?
Solution:

Long Numericals
Question 1: A cell of e.m.f. 1.5 V and internal resistance 1.0 W is connected to two resistors of 4.0 W and 20.0 in series as shown in the figure:
Calculate the:
(i) Current in the circuit.
(ii) Potential difference across the 4.0 ohm resistor.
(iii) Voltage drop when the current is flowing.
(iv) Potential difference across the cell.
(i) E.m.f. of cell = 1.5 volt, Internal resistance = 1.0 ohm
Solution: (i) E.m.f. of cell = 1.5 volt, Internal resistance = 1.0 ohm

Question 2: A 10 m long wire of a particular material is of reistance 5Ω What will be the resistance: (i) of 5m long wire of same material and same thickness, (ii) of 10m long wire of same material but the double radius (iii) If the wire is doubled itself, (iv) if the wire is stretched to double its length?
Solution:

Question 3: Three resistances, of which two are equal when connected in series have an effective resistance of 30 ohms. When the three resistances are connected in parallel, the effective resistances is 3 ohms. Find the values of the individual resistances.
Solution:

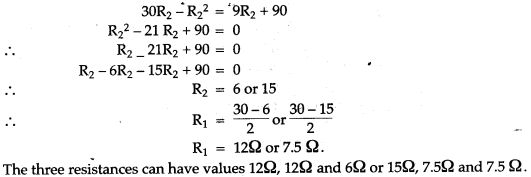
Question 4: When a resistance of 3Ω is connected across a cell, the current flowing is 0.5 A. On changing the resistance to 7Ω, the current becomes 0.25A. Calculate the e.m.f. and the internal resistance of the cell.
Solution:

For More Resources