Arithmetic Sequences and Series
A sequence is an ordered list of numbers.
The sum of the terms of a sequence is called a series.


Read More:
While some sequences are simply random values, other sequences have a definite pattern that is used to arrive at the sequence’s terms.
Two such sequences are the arithmetic and geometric sequences. Let’s investigate the arithmetic sequence.
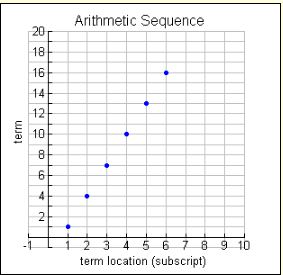
If a sequence of values follows a pattern of adding a fixed amount from one term to the next, it is referred to as an arithmetic sequence. The number added to each term is constant (always the same).
The fixed amount is called the common difference, d, referring to the fact that the difference between two successive terms yields the constant value that was added. To find the common difference, subtract the first term from the second term.
Notice the linear nature of the scatter plot of the terms of an arithmetic sequence. The domain consists of the counting numbers 1, 2, 3, 4, … and the range consists of the terms of the sequence. While the x value increases by a constant value of one, the y value increases by a constant value of 3 (for this graph).

Examples:
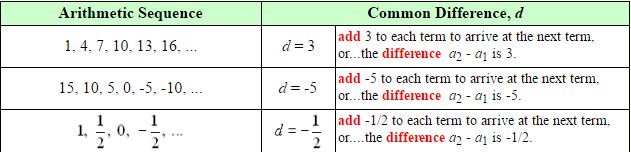
Formulas used with arithmetic sequences and arithmetic series:

Examples:

