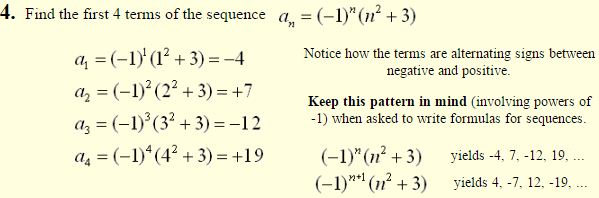Sequences
In the previous lesson, we learned about pattern of numbers. In this lesson we discuss about Sequences.
A sequence is an ordered list of numbers.

The sum of the terms of a sequence is called a series.
- Each number of a sequence is called a term (or element) of the sequence.
- A finite sequence contains a finite number of terms (you can count them). 1, 4, 7, 10, 13
- An infinite sequence contains an infinite number of terms (you cannot count them). 1, 4, 7, 10, 13, . . .
- The terms of a sequence are referred to in the subscripted form shown below, where the natural number subscript refers to the location (position) of the term in the sequence.

(If you study computer programming languages such as C, C++, and Java,
you will find that the first position in their arrays (sequences) start with a subscript of zero.)
The general form of a sequence is represented:
- The domain of a sequence consists of the counting numbers 1, 2, 3, 4, … and the range consists of the terms of the sequence.
- The terms in a sequence may, or may not, have a pattern, or a related formula.
- For some sequences, the terms are simply random.
Let’s examine some sequences that have patterns:
Sequences often possess a definite pattern that is used to arrive at the sequence’s terms.
It is often possible to express such patterns as a formula. In the sequence shown at the left, an explicit formula may be:
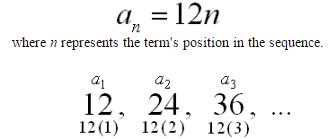
Examples: