What Is Arithmetic Progression
Arithmetic Progression (A.P.)
Arithmetic Progression is defined as a series in which difference between any two consecutive terms is constant throughout the series. This constant difference is called common difference.
A sequence of numbers < tn > is said to be in arithmetic progression (A.P.) when the difference tn – tn–1 is a constant for all n ∈ N. This constant is called the common difference of the A.P. and is usually denoted by the letter d.
If ‘a’ is the first term and ‘d’ the common difference, then an A.P. can be represented as a + (a + d) + (a + 2d) + (a + 3d) + ……

Example : 2, 7, 12, 17, 22, …… is an A.P. whose first term is 2 and common difference 5.
Algorithm to determine whether a sequence is an A.P. or not.
Step I: Obtain an (the nth term of the sequence).
Step II: Replace n by n – 1 in an to get an–1.
Step III: Calculate an – an–1.
If an – an–1 is independent from n, the given sequence is an A.P. otherwise it is not an A.P.
∴ tn = An + B represents the nth term of an A.P. with common difference A.
Note: If a,b,c, are in AP ⟺ 2b = a + c
General term of an A.P.
(1) Let ‘a’ be the first term and ‘d’ be the common difference of an A.P. Then its nth term is a + (n– 1) d i.e., Tn = a + (n– 1) d.
(2) rth term of an A.P. from the end: Let ‘a’ be the first term and ‘d’ be the common difference of an A.P. having n terms. Then rth term from the end is (n – r + 1)th term from the beginning
i.e., rth term from the end = T(n-r+1) = a + (n – r)d.
If last term of an A.P. is l then rth term from end = l – (r – 1)d.
Selection of terms in an A.P.
When the sum is given, the following way is adopted in selecting certain number of terms :
| Number of terms | Terms to be taken |
| 3 | a – d, a, a + d |
| 4 | a – 3d, a – d, a + d, a + 3d |
| 5 | a – 2d, a – d, a, a + d, a + 2d |
In general, we take a – rd, a – (r – 1)d, ……., a – d, a, a + d, ……, a + (r – 1)d, a + rd, in case we have to take (2r + 1) terms (i.e. odd number of terms) in an A.P.
And, a – (2r – )d, a – (2r – 3)d,…….., a – d, a + d, ……, a + (2r – 1)d in case we have to take 2r terms in an A.P.
When the sum is not given, then the following way is adopted in selection of terms.
| Number of terms | Terms to be taken |
| 3 | a, a + d, a + 2d |
| 4 | a, a + d, a + 2d, a + 3d |
| 5 | a, a + d, a + 2d, a + 3d, a + 4d |
Sum of n terms of an A.P.
The sum of n terms of the series a, (a + d), (a + 2d), (a + 3d), …… {a + (n – 1)d} is given by
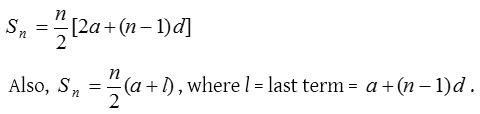
Arithmetic mean
If a, A, b are in A.P., then A is called A.M. between a and b.
(1) If a, A1, A2, A3, ….. An, b are in A.P., then A1, A2, A3, ….. An are called n A.M.’s between a and b.
(2) Insertion of arithmetic means
(i) Single A.M. between a and b :
If a and b are two real numbers then single A.M. between a and b = \(\frac { a+b }{ 2 }\)
(ii) n A.M.’s between a and b : If A1, A2, A3, ….. An are n A.M.’s between a and b, then
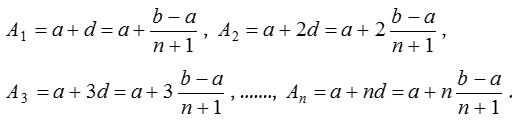
Properties of A.P.
- If a1, a2, a3, …… are in A.P. whose common difference is d, then for fixed non-zero number k ∈ R.
- a1 ± k, a2 ± k, a3 ± k, .….. will be in A.P., whose common difference will be d.
- ka1, ka2, ka3, …… will be in A.P. with common difference = kd.
- a1/k, a2/k, a3/k, ……will be in A.P. with common difference = d/k.
- The sum of terms of an A.P. equidistant from the beginning and the end is constant and is equal to sum of first and last term. i.e. a1 + an = a2 + an−1 = a3 + an−2 = …..
- If number of terms of any A.P. is odd, then sum of the terms is equal to product of middle term and number of terms.
- If number of terms of any A.P. is even then A.M. of middle two terms is A.M. of first and last term.
- If the number of terms of an A.P. is odd then its middle term is A.M. of first and last term.
- If a1, a2,…… an and b1, b2,…… bn are the two A.P.’s. Then a1 ± b1, a2 ± b2,.….. an ± bn are also A.P.’s with common difference d1 ≠ d2, where d1 and d2 are the common difference of the given A.P.’s.
- Three numbers a, b, c are in A.P. iff 2b = a + c.
- If Tn, Tn+1, and Tn+2 are three consecutive terms of an A.P., then 2Tn+1 = Tn + Tn+2.
- If the terms of an A.P. are chosen at regular intervals, then they form an A.P.
How to Find nth Term in Arithmetic Progression With Examples
Example 1: Find 26th term from last of an AP 7, 15, 23……., 767 consits 96 terms.
Solution. Method: I
rth term from end is given by
= Tn – (r – 1) d or
= (n – r + 1)th term from beginning where n is total no. of terms.
m = 96, n = 26
∴ T26 from last = T(96-26+1) from beginning
= T71 from beginning
= a + 70d
= 7 + 70 (8) = 7 + 560 = 567
Method: II
d = 15 – 7 = 8
∴ from last, a = 767 and d = –8
∴ T26 = a + 25d = 767 + 25 (–8)
= 767 – 200
= 567.
Example 2: If the nth term of a progression be a linear expression in n, then prove that this progression is an AP.
Solution. Let the nth term of a given progression be given by
Tn = an + b, where a and b are constants.
Then, Tn-1 = a(n – 1) + b = [(an + b) – a]
∴ (Tn – Tn-1) = (an + b) – [(an + b) – a] = a,
which is a constant.
Hence, the given progression is an AP.
Example 3: Write the first three terms in each of the sequences defined by the following –
(i) an = 3n + 2 (ii) an = n2 + 1
Solution. (i) We have,
an = 3n + 2
Putting n = 1, 2 and 3, we get
a1 = 3 × 1 + 2 = 3 + 2 = 5,
a2 = 3 × 2 + 2 = 6 + 2 = 8,
a3 = 3 × 3 + 2 = 9 + 2 = 11
Thus, the required first three terms of the sequence defined by an = 3n + 2 are 5, 8, and 11.
(ii) We have,
an = n2 + 1
Putting n = 1, 2, and 3 we get
a1 = 12 + 1 = 1 + 1 = 2
a2 = 22 + 1 = 4 + 1 = 5
a3 = 32 + 1 = 9 + 1 = 10
Thus, the first three terms of the sequence defined by an = n2 + 1 are 2, 5 and 10.
Example 4: Write the first five terms of the sequence defined by an = (–1)n-1 . 2n
Solution. an = (–1)n-1 × 2n
Putting n = 1, 2, 3, 4, and 5 we get
a1 = (–1)1-1 × 21 = (–1)0 × 2 = 2
a2 = (–1)2-1 × 22 = (–1)1 × 4 = – 4
a3 = (–1)3-1 × 23 = (–1)2 × 8 × 8
a4 = (–1)4-1 × 24 = (–1)3 × 16 = –16
a5 = (–1)5-1 × 25 = (–1)4 × 32 = 32
Thus the first five term of the sequence are 2, –4, 8, –16, 32.
Example 5: The nth term of a sequence is 3n – 2. Is the sequence an A.P. ? If so, find its 10th term.
Solution. We have an = 3n – 2
Clearly an is a linear expression in n. So, the given sequence is an A.P. with common difference 3.
Putting n = 10, we get
a10 = 3 × 10 – 2 = 28
Example 6: Find the 12th, 24th and nth term of the A.P. given by 9, 13, 17, 21, 25, ………
Solution. We have,
a = First term = 9 and, d = Common difference = 4
[∵ 13 – 9 = 4, 17 – 13 = 4, 21 – 7 = 4 etc.]
We know that the nth term of an A.P. with first term a and common difference d is given by an = a + (n – 1) d
Therefore,
a12 = a + (12 – 1) d = a + 11d = 9 + 11 × 4 = 53
a24 = a + (24 – 1) d = a + 23 d = 9 + 23 × 4 = 101
and, an = a + (n – 1) d = 9 + (n – 1) × 4 = 4n + 5
a12 = 53, a24 = 101 and an = 4n + 5
Example 7: Which term of the sequence –1, 3, 7, 11, ….. , is 95 ?
Solution. Clearly, the given sequence is an A.P.
We have,
a = first term = –1 and, d = Common difference = 4.
Let 95 be the nth term of the given A.P. then,
an = 95
⇒ a + (n – 1) d = 95
⇒ – 1 + (n – 1) × 4 = 95
⇒ – 1 + 4n – 4 = 95 ⇒ 4n – 5 = 95
⇒ 4n = 100 ⇒ n = 25
Thus, 95 is 25th term of the given sequence.
Example 8: Which term of the sequence 4, 9 , 14, 19, …… is 124 ?
Solution. Clearly, the given sequence is an A.P. with first term a = 4 and common difference d = 5.
Let 124 be the nth term of the given sequence. Then, an = 124
a + (n – 1) d = 124
⇒ 4 + (n – 1) × 5 = 124
⇒ n = 25
Hence, 25th term of the given sequence is 124.
Example 9: The 10th term of an A.P. is 52 and 16th term is 82. Find the 32nd term and the general term.
Solution. Let a be the first term and d be the common difference of the given A.P. Let the A.P. be
a1, a2, a3, ….. an, ……
It is given that a10 = 52 and a16 = 82
⇒ a + (10 – 1) d = 52 and a + (16 – 1) d = 82
⇒ a + 9d = 52 ….(i)
and, a + 15d = 82 ….(ii)
Subtracting equation (ii) from equation (i), we get
–6d = – 30 ⇒ d = 5
Putting d = 5 in equation (i), we get
a + 45 = 52 ⇒ a = 7
∴ a32 = a + (32 – 1) d = 7 + 31 × 5 = 162
and, an = a + (n – 1) d = 7 (n – 1) × 5 = 5n + 2.
Hence a32 = 162 and an = 5n + 2.
Example 10: Determine the general term of an A.P. whose 7th term is –1 and 16th term 17.
Solution. Let a be the first term and d be the common difference of the given A.P. Let the A.P. be a1, a2, a3, ……. an, …….
It is given that a7 = – 1 and a16 = 17
a + (7 – 1) d = – 1 and, a + (16 – 1) d = 17
⇒ a + 6d = – 1 ….(i)
and, a + 15d = 17 ….(ii)
Subtracting equation (i) from equation (ii), we get
9d = 18 ⇒ d = 2
Putting d = 2 in equation (i), we get
a + 12 = – 1 ⇒ a = – 13
Now, General term = an
= a + (n – 1) d = – 13 + (n – 1) × 2 = 2n – 15
Example 11: If five times the fifth term of an A.P. is equal to 8 times its eight term, show that its 13th term is zero.
Solution. Let a1, a2, a3, ….. , an, …. be the A.P. with its first term = a and common difference = d.
It is given that 5a5 = 8a8
⇒ 5(a + 4d) = 8 (a + 7d)
⇒ 5a + 20d = 8a + 56d ⇒ 3a + 36d = 0
⇒ 3(a + 12d) = 0 ⇒ a + 12d = 0
⇒ a + (13 – 1) d = 0 ⇒ a13 = 0
Example 12: If the mth term of an A.P. be 1/n and nth term be 1/m, then show that its (mn)th term is 1.
Solution. Let a and d be the first term and common difference respectively of the given A.P. Then,
1/n= mth term ⇒ 1/n = a + (m – 1) d ….(i)
1/m = nth term ⇒ 1/m = a + (n – 1) d ….(ii)
On subtracting equation (ii) from equation (i), we get
\( \frac{1}{n}-\frac{1}{m}=~\left( mn \right)d \)
\( \Rightarrow \frac{m-n}{mn}=~\left( mn \right)d\Rightarrow d=\frac{1}{mn} \)
\( ~\text{Putting d}=~\frac{1}{mn}\text{in equation }\left( \text{i} \right)\text{, we get} \)
\( \frac{1}{n}=a+\frac{(m-1)}{mn}\Rightarrow a=\frac{1}{mn} \)
∴ (mn)th term = a + (mn – 1) d
\( =\frac{1}{mn}+(mn-1)\frac{1}{mn}=1 \)
Example 13: If m times mth term of an A.P. is equal to n times its nth term, show that the (m + n) term of the A.P. is zero.
Solution. Let a be the first term and d be the common difference of the given A.P. Then, m times mth term = n times nth term
⇒ mam = nan
⇒ m{a + (m – 1) d} = n {a + (n – 1) d}
⇒ m{a + (m – 1) d} – n{a + (n – 1) d} = 0
⇒ a(m – n) + {m (m – 1) – n(n – 1)} d = 0
⇒ a(m – n) + (m – n) (m + n – 1) d = 0
⇒ (m – n) {a + (m + n – 1) d} = 0
⇒ a + (m + n – 1) d = 0
⇒ am+n = 0
Hence, the (m + n)th term of the given A.P. is zero.
Example 14: If the pth term of an A.P. is q and the qth term is p, prove that its nth term is (p + q – n).
Solution. Let a be the first term and d be the common difference of the given A.P. Then,
pth term = q ⇒ a + (p – 1) d = q ….(i)
qth term = p ⇒ a + (q – 1) d = p ….(ii)
Subtracting equation (ii) from equation (i),
we get
(p – q) d = (q – p) ⇒ d = – 1
Putting d = – 1 in equation (i), we get
a = (p + q – 1)
nth term = a + (n – 1) d
= (p + q – 1) + (n – 1) × (–1) = (p + q – n)
Example 15: If pth, qth and rth terms of an A.P. are a, b, c respectively, then show that
(i) a (q – r) + b(r – p) + c(p – q) = 0
(ii) (a – b) r + (b –¬ c) p + (c – a) q = 0
Solution. Let A be the first term and D be the common difference of the given A.P. Then,
a = pth term ⇒ a = A + (p – 1) D ….(i)
b = qth term ⇒ b = A + (q – 1) D ….(ii)
c = rth term ⇒ c = A+ (r – 1) D ….(iii)
(i) We have,
a(q – r) + b (r – p) + c (p – q)
= {A + (p – 1) D} (q – r) + {A + (q – 1)} (r – p) + {A + (r – 1) D} (p – q)
[Using equations (i), (ii) and (iii)]
= A {(q – r) + (r – p) + (p – q)} + D {(p – 1) (q – r) + (q – 1) (r – p) + (r – 1) (p – q)}
= A {(q – r) + (r – p) + (p – q)} + D{(p – 1) (q – r) + (q – 1) (r – p) + (r – 1) (p – q)}
= A . 0 + D {p (q – r) + q (r – p) + r (p – q) – (q – r) – (r – p) – (p – q)}
= A . 0 + D . 0 = 0
(ii) On subtracting equation (ii) from equation (i), equation (iii) from equation (ii) and equation (i) from equation (iii), we get
a – b = (p – q) D, (b – c) = (q – r) D and c – a = (r – p) D
∴ (a – b) r + (b – c) p + (c – a) q
= (p – q) Dr + (q – r) Dp + (r – p) Dq
= D {(p – q) r + (q – r) p + (r – p) q}
= D × 0 = 0
Example 16: Determine the 10th term from the end of the A.P. 4, 9, 14, …….., 254.
Solution. We have,
l = Last term = 254 and,
d = Common difference = 5,
10th term from the end = l – (10 – 1) d
= l – 9d = 254 – 9 × 5 = 209.
Example 17: Four numbers are in A.P. If their sum is 20 and the sum of their square is 120, then find the middle terms.
Solution. Let the numbers are a – 3d, a – d, a + d, a + 3d
given a – 3d + a – d + a + d + a + 3d = 20
⇒ 4a = 20 ⇒ a = 5
and (a – 3d)2 + (a – d)2 + (a + d)2 + (a + 3d)2 = 120
4a2 + 20 d2 = 120
4 × 52 + 20 d2 = 120
d2 = 1 ⇒ d = ±1
Hence numbers are 2, 4, 6, 8
Example 18: Find the common difference of an AP, whose first term is 5 and the sum of its first four terms is half the sum of the next four terms.
Sol. a1 + a2 + a3 + a4 = (a5 + a6 + a7 + a8)
⇒ 2[a1 + a2 + a3 + a4] = a5 + a6 + a7 + a8
⇒ 2[a1 + a2 + a3 + a4] + (a1 + a2 + a3 + a4) = [a1 + a2 + a3 + a4]+ (a5 + a6 + a7 + a8)
(adding both side a1 + a2 + a3 + a4)
⇒ 3(a1 + a2 + a3 + a4) = a1 + …. + a8 ⇒ 3S4 = S8
\(\Rightarrow 3\left[ \frac{4}{2}(2\times 5+(4-1)\,\,d \right]=\left[ \frac{8}{2}(2\times 5+(8-1)\,\,d \right]\)
⇒ 3[10 + 3d] = 2[10 + 7d]
⇒ 30 + 9d = 20 + 14d ⇒ 5d = 10 ⇒ d = 2
Example 19: If the nth term of an AP is (2n + 1) then find the sum of its first three terms.
Sol. ∵ an = 2n + 1
a1 = 2(1) + 1 = 3
a2 = 2(2) + 1 = 5
a3 = 2(3) + 1 = 7
∴ a1 + a2 + a3 = 3 + 5 + 7 = 15