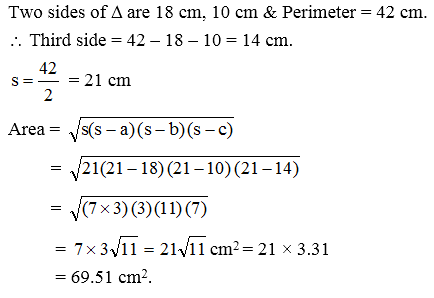How To Find Area Of Trapezium

Area Of Trapezium Example Problems With Solutions

Trapezium – A quadrilateral which has one pair of opposite sides parallel.

Example 1:    Find the area of a trapezium whose parallel sides 25 cm, 13 cm and other sides are 15 cm and 15 cm
Solution:

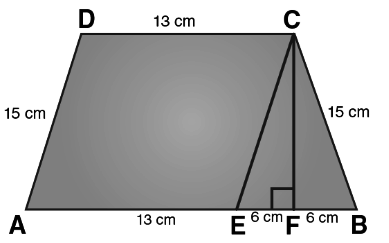
In ΔCEF,
CE = 10 cm and EF = 6cm
Using Pythagoras theorem:
CE² = CF² + EF²
CF² = CE² – EF²
CF² = 15² – 6²
CF² = 225-36
CF² = 189
CF = √189
= √ (9×21)
= 3√21 cm
From the figure we can write,
Area of trapezium = Area of parallelogram AECD + Area of area of triangle CEF
Area of trapezium = height + $\frac { 1 }{ 2 }$ (sum of parallel sides)
Area of trapezium = 3√21 × $\frac { 1 }{ 2 }$ (25 + 13)
Area of trapezium = 3√21 × 19 = 57√21
∴ Area of trapezium = 57√21 cm²

Example 2:    A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m. The nonparallel sides are 14 m and 13 m. Find the area of the field.
Solution:
Let ABCD be a trapezium with, AB∥CD

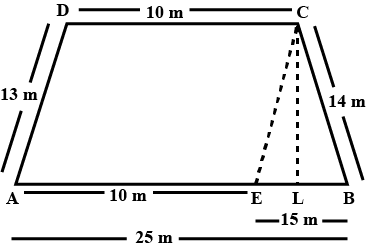
AB = 25m
CD = 10m
BC = 14m
AD = 13m
Draw CE∥DA. So, ADCE is a parallelogram with,
CD = AE = 10m
CE = AD = 13m
BE = AB − AE = 25 − 10 = 15m
In ΔBCE, the semi perimeter will be,

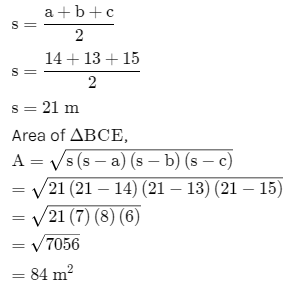
Also, area of ΔBCE is,

Therefore, the area of the trapezium is 196 m²

Example 3:    Students of a school staged a rally for cleanliness compaign. They walked through the lanes in two groups. One group walked through the lanes AB, BC and CA, while other through AC, CD and DA (see fig.). Then they cleaned the area enclosed within their lanes. If AB = 9 m, BC = 40 m, CD = 15 m, DA = 28 m, and ∠B = 90°. Which group cleaned more area and by how much? Find the total area cleaned by the students.
Solution:
Given, ΔABC is a right-angled triangle.

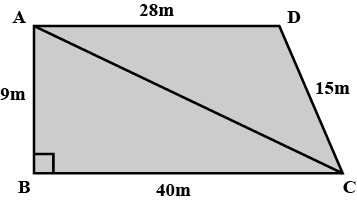
Therefore, AC² = AB² + BC²  … [Using Pythagoras Theorem]

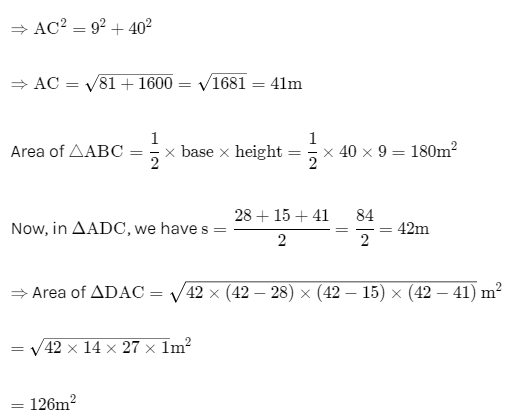
So, group 1 covered area ΔABC=180m² and group 2 covered area ΔDAC = 126m²
Hence, group 1 covers more area by group 2 which is 54m² = (180m² − 126m²) more.
Now, area covered by both the groups = Area ABC + Area DAC = 180m² + 126m² = 306m²

Example 4:    Radha made a picture of an aeroplane with coloured paper as shown in figure. Find the total area of the paper used.

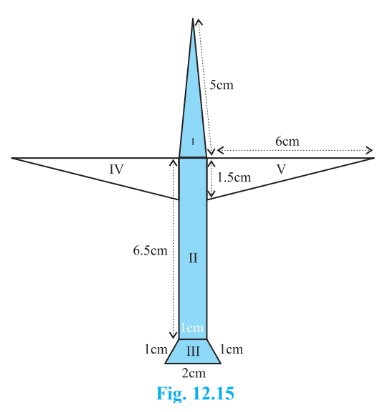
Solution:




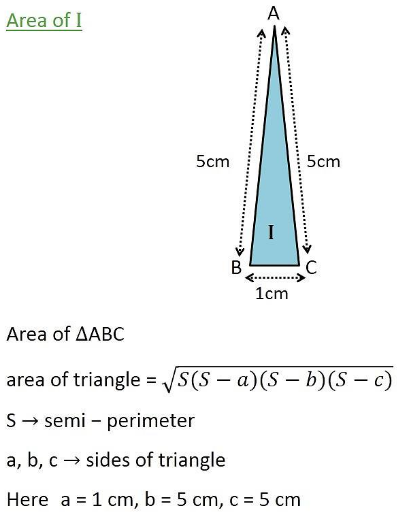
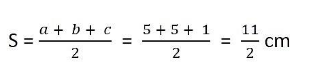
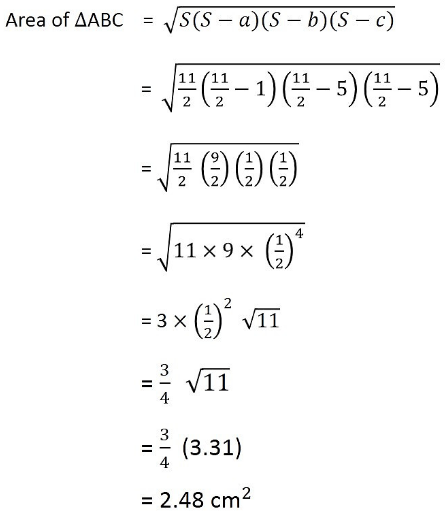
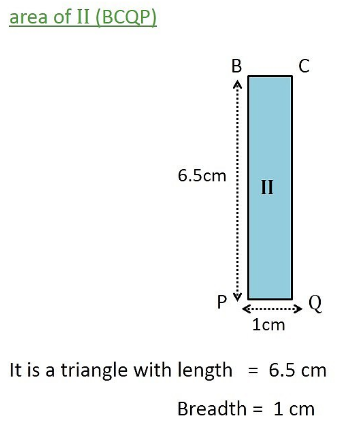
Area of Rectangle = Length × bredth
= 6.5 × 1 =6.5 cm²

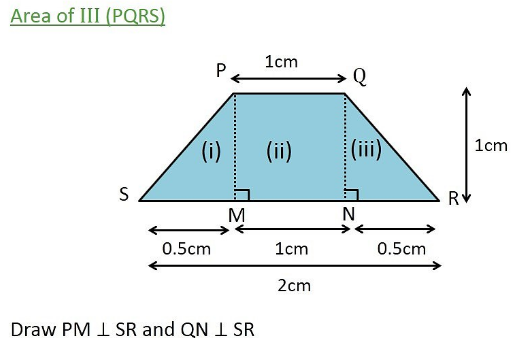
Hence we have the following
Area of III = Area of I + Area of II + Area of III
I and III are right angled triangles.
area (I) +area (II) = 2 area (I) (By symmetry)
= 2 × $\frac { 1 }{ 2 }$ × 0.5 × 1
= 0.5 cm²

(II) is a rectangle
∴ Area (II) = Length × bredth
= 1 × 1 = 1 cm²

Area of III = Area of I + Area of II + Area of III
= 0.5 × 1 = 1.5 cm²

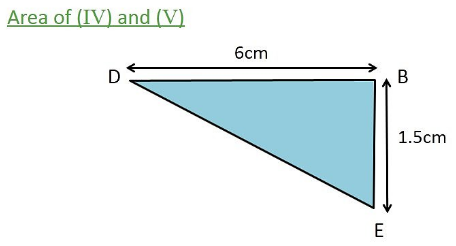
(IV) and (V) are similar right angled triangles.
Area of (IV) = Area of (V) = $\frac { 1 }{ 2 }$ × Base × Height
= $\frac { 1 }{ 2 }$ × 1.5 × 6
= 3 × 1.5
= 4.5 cm²

Thus,
Area = Area of I + Area of II + Area of III + Area of IV + Area of V
= 2.48 + 6.5 + 1.5 + 4.5 + 4.5
= 2.48 + 8.0 + 9.0
= 17.0 + 2.48
= 19.48 cm²
= 19.4 cm²

Example 5:    An umbrella is made by stitching 10 triangular pieces of cloth of two different colours (see figure), each piece measuring 20 cm, 50 cm and 50 cm. How much cloth of each colour is required for the umbrella?

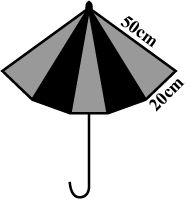
Solution:
There are 10 triangles, out of which 5 of black and 5 of grey color. Now,
Area of of each cloth = 5 × area of 1 triangle

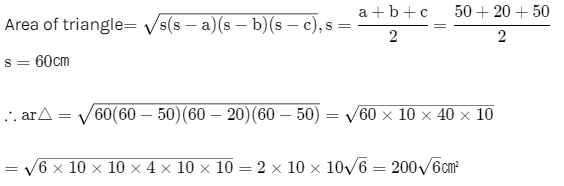
Area of each cloth required = (5 × 200√6) = 1000√6 cm²

Example 6:    A floral design on a floor is made up of 16 tiles which are triangular, the sides of the triangle being 9 cm, 28 cm and 35 cm (see figure). Find the cost of polishing the tiles at the rate of 50 paisa per cm².

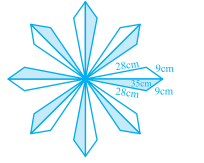
Solution:
Given that
a = 35cm, b = 28cm, c = 9cm

= 36 × 2.45 = 88.2 cm²
Area of total 16 tiles = 16 × 88.2 = 1411.2 cm²
Cost of polishing per cm² area = 50p
Cost of polishing 1411.2 cm² area = Rs. 50 × 1411.2 = Rs. 705.60

Example 7:    Sanya has a piece of land which is in the shape of a rhombus. She wants her one daughter and one son to work on the land and produce different crops to suffice the needs of their family. She divided the land in two equals parts. If the perimeter of the land is 400 m and one of the diagonals is 160 m, how much area each of them will get ?
Solution:

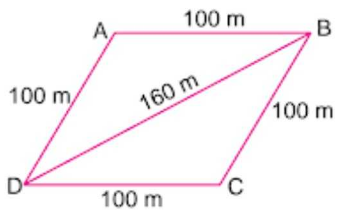
Let ABCD be the field. Given perimeter = 400 m
So, each side = $\frac { 400 }{ 4 }$ = 100 m
Diagonal BD = 160 m
Let a = 100 m, b = 100 m, c = 160 m


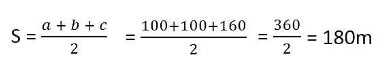
Hence, each of the two children will get an area of 4800 m².

Example 8:    There is a slide in a park. One of its side walls has been painted in some colour with a message ‘‘KEEP THE PARK GREEN AND CLEAN’’ (see figure). If the sides of the wall are 15 m, 11 m and 6 m, find the area painted in colour.

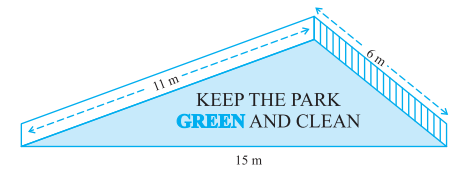
Solution:
Given that
Sides: a = 15m, b = 11m and c = 6m


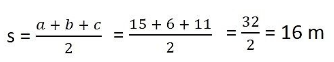
∴ The area painted in color is = 20√2 m²

Example 9:    A triangular park ABC has sides 120 m, 80 m and 50 m (see fig.). A gardener Dhania has to put a fence all around it and also plant grass inside. How much area does she need to plant? Find the cost of fencing it with barbed wire at the rate of 20 per metre leaving a space 3m wide for a gate on one side.
Solution:    Computation of area:

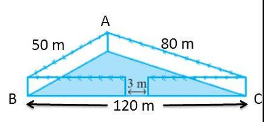
Clearly, the park is triangular with sides
a = BC = 120 m, b = CA = 80 m and
c = AB = 50 m

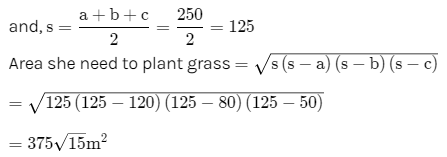
Number of meters to be fenced = 50 + 80 + 120 – 3
= 250 – 3 = 247 m
cost of fencing = Rs 20 per metre.
cost of fencing park = Rs 20 × 247
= Rs 4940

Example 10:    The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 122 m, 22 m and 120 m (see fig.). The advertisements yield an earning of 5000 per m² per year. A company hired both walls for 3 months. How much rent did it pay ?

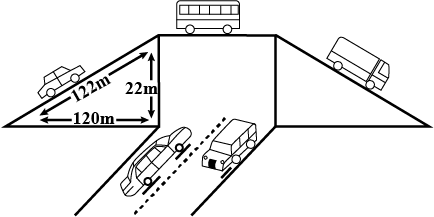
Solution:
In ΔABC
a = 122m, b = 22m, c = 120m

Example 11:    Sides of a triangle are in the ratio of 12 : 17 : 25  and its perimeter is 540 cm. Find its area.
Solution:
Let x be common ratio
∴ Sides of triangle will be: 12x, 17x and 25x
Perimeter = 540 cm(given)
⇒ 12x + 17x + 25x = 540 cm,
⇒ 54x = 540 cm
⇒ x = 10 cm
∴ Sides of triangle: a=120,b=170,c=250 cms
⇒ 2s = 540
⇒ s = 270 cm

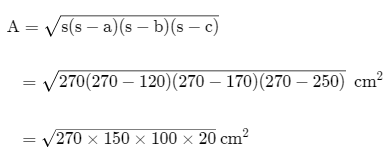
∴ A = 9000 cm²

Example 12:    Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is
42 cm.
Solution: