How do you Add and Subtract Rational Numbers?

How do you Add and Subtract Rational Numbers?

There are four basic operations on rational numbers :

1. Addition
2. Subtraction
3. Multiplication
4. Division.

Addition of Rational Numbers

If two rational numbers are to be added, we first express each one of them as rational number with positive denominator.
There are two possibilities :
(1) Either they have same denominators, or
(2) They have different denominators.

Adding Rational Numbers with Same Denominator:

Let us add \(\frac { 8 }{ 5 }\) and \(\frac { -6 }{ 5 }\)
Represent the numbers on the number line.

Here, the distance between two consecutive points is \(\frac { -6 }{ 5 }\). For  \(\frac { 8 }{ 5 }\), move 6 steps to the left of \(\frac { 8 }{ 5 }\) and we reach at \(\frac { 2 }{ 5 }\).

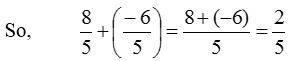
Example 1: Add : \(\frac { -5 }{ 9 }\) and \(\frac { -17 }{ 9 }\).
Solution:
Given rational numbers are \(\frac { -5 }{ 9 }\) and \(\frac { -17 }{ 9 }\).
Adding these two numbers, we have

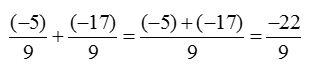
Which is the required answer.

Example 2: Add : \(\frac { -23 }{ 28 }\) and \(\frac { 5 }{ -28 }\).
Solution:
We first express \(\frac { 5 }{ -28 }\) as a rational number with positive denominator.

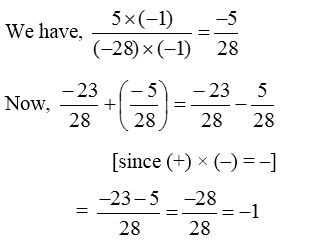
Addition of Rational numbers with Different Denominators:
In this case, we convert the given rational numbers to a common denominator and then add.

Examples:

1. Add \(\frac { 8 }{ -5 }\) and \(\frac { 4 }{ -3 }\).
Solution:
The given rational numbers are \(\frac { 8 }{ -5 }\) and \(\frac { 4 }{ -3 }\). Clearly, they have different denominators. Here, first we express the given rational numbers into standard forms.

Which is the required answer.

2. Add : \(\frac { 8 }{ 10 }\), 3.
Solution: 

3. Simplify : \(\frac { 4 }{ 3 } +\frac { 3 }{ 5 } +\frac { -2 }{ 5 } +\frac { -11 }{ 3 }\)
Solution:

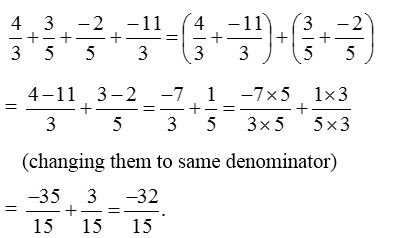
4. Add \(\frac { 7 }{ 9 }\) and \(\frac { -5 }{ 9 }\).
Solution:

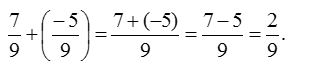
In case, if denominator of the rational number is negative, first we make it (denominator) Positive and then add.

5. Add : \(\frac { 6 }{ -5 }\) and \(\frac { 4 }{ 5 }\).
Solution:

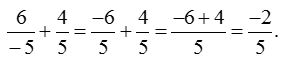
6. Find the sum of \(\frac { -8 }{ 5 }\) and \(\frac { -5 }{ 3 }\)
Solution:

Note : Addition of rational numbers is closure (the sum is also rational) commutative (a + b = b + a) and associative(a + (b + c)) = ((a + b) + c).

Additive inverse:
The negative of a rational number is called additive inverse of the given number.
Note: Zero is the only rational no. which is its even negative or inverse.

Subtraction of Rational Numbers

If we add the additive inverse of a rational number and other rational number then this is called subtraction of two rational numbers. So the subtraction is inverse process of addition and the term add the negative of use for subtraction.

Subtraction of Rational Numbers Problems with Solutions

1. Find value of \(\frac { 2 }{ 3 } -\frac { 4 }{ 5 }\).
Solution:

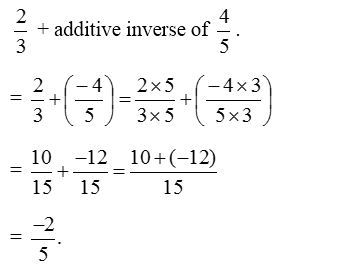
2. Find value of \(\frac { 2 }{ 7 } -\left( \frac { -5 }{ 3 }  \right)\).
Solution:

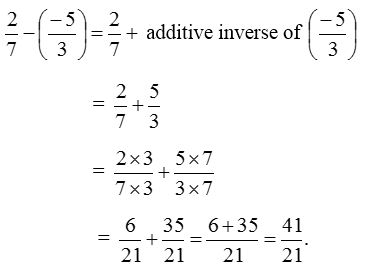
3. Subtract \(\frac { -5 }{ 8 }\) from \(\frac { -3 }{ 7 }\).
Solution:

4. Simplify : \(\frac { 1 }{ 6 } +\frac { -2 }{ 5 } -\frac { -2 }{ 15 }\).
Solution:

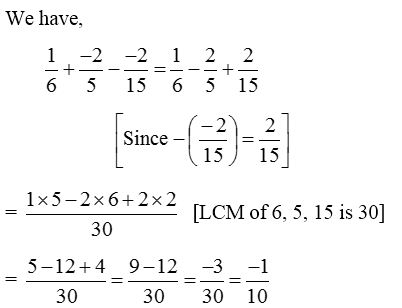
5. What number should be added to \(\frac { -5 }{ 8 }\) so that the sum is \(\frac { 5 }{ 9 }\)?
Solution:

6. What number should be subtracted from \(\frac { 27 }{ 11 }\) so as to get \(\frac { -5 }{ 33 }\)?
Solution:

7. The sum of two rational numbers is \(\frac { -3 }{ 5 }\) If one of them is \(\frac { -9 }{ 10 }\) Find the other.
Solution:

Maths