What is a Ratio and Proportion


RATIO
In our day-to-day life, we compare one quantity with another quantity of the same kind by using the ‘method of subtraction’ and ‘method of division’.
Example: The height of Seema is 1 m 67 cm and that of Reema is 1 m 62 cm. The difference in their heights is:
167 cm – 162 cm = 5 cm
Thus, we say Seema is 5 cm taller than Reema.
Similarly, suppose the weight of Seema is 60 kg and the weight of Reema is 50 kg. We can compare their weights by division, i.e.,
\(\frac{\text{Weight of Seema}}{\text{Weight of Reema}}=\frac{\text{50 kg}}{\text{60 kg}}\)
\(=\frac { 6 }{ 5 }\)
So, the weight of Seema is \(\frac { 6 }{ 5 }\) times the weight of Reema.
When we compare two similar quantities by division, the comparison is called the ‘ratio’. It is denoted by ‘:’ and read as ‘is to’.
Example: \(\frac { 5 }{ 8 }\) = 5 : 8 (read as 5 is to 8).
As shown in the above example a ratio is like a fraction or comparison of two numbers, where a numerator and a denominator is separated by a colon (:). The first term or the quantity (5), called antecedent means ‘that precedes’ and the second term, called consequent means ‘that follows’.
Read More:
Ratio and Proportion Rs Aggarwal Class 7 Solutions
Ratio and Proportion Rs Aggarwal Class 6 Solutions
Properties of Ratio
When we compare two quantities, the following points must be taken care of:
- A ratio is usually expressed in its simplest form.
Example:
\(\frac{12}{36}=\frac{1}{3}=1:3\) - Both the quantities should be in the same unit. So, ratio is a number with no unit involved in it.
Example: 200 g : 2 kg
= 200 g : 2000 g
\(\frac{200}{2000}=\frac{1}{10}=1:10\) - The order of the quantities of a ratio is very important.
Example: 5 : 6 is different from 6 : 5.
They are not equal.
5 : 6 ≠ 6 : 5
Equivalent Ratios
A ratio is similar to a fraction. So, if we divide or multiply the numerator (antecedent) and denominator (consequent) by the same number, we get an equivalent fraction (ratio).
Example: 5 : 6 = \(\frac { 5 }{ 6 }\)
Comparison of Ratios
To compare two ratios, we have to follow these steps:
Step 1: Convert each ratio into a fraction in its simplest form.
Step 2: Find the LCM of denominators of the fractions obtained in step 1.
Step 3: Convert the denominators equal to LCM obtained in step 2 in each fraction.
Step 4: Now, compare the numerators of the fractions; the fraction with a greater numerator will be greater than the other.
Example 1: Compare the ratio 5: 6 and 7: 9.
Solution:
Express the given ratios as fraction
5 : 6 = \(\frac { 5 }{ 6 } \) and 7 : 9 = \(\frac { 7 }{ 9 } \)
Now find the L.C.M (least common multiple) of 6 and 9
The L.C.M (least common multiple) of 6 and 9 is 18.
Making the denominator of each fraction equal to 18, we have
\(\frac { 5 }{ 6 } \) = (5 ×3)/(6 ×3) = \(\frac { 15 }{ 18 } \) and \(\frac { 7 }{ 9 } \) = (7 ×2)/(9 ×2) = \(\frac { 14 }{ 18 } \)
Clearly, 15 > 14
Now, \(\frac { 15 }{ 18 } \) > \(\frac { 14 }{ 18 } \)
Therefore, 5 : 6 > 7 : 9.
Example 2: Convert the ratio 275 : 125 in its simplest form.
Solution:
Find the GCD (or HCF) of numerator and denominator
GCD of 275 and 125 is 25
Divide both the numerator and denominator by the GCD
\(\frac{275 \div 25}{125 \div 25}\)
Reduced fraction:
\(\frac { 11 }{ 5 } \)
Therefore, \(\frac { 275 }{ 125 } \) simplified to lowest terms is \(\frac { 11 }{ 5 } \).
Example 3: Write the following ratios in descending order:
1 : 3, 5 : 12, 4 : 15 and 2 : 3
Solution: We have,
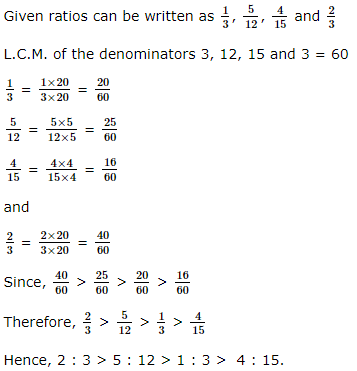
Example 4: Mr Lai divides a sum of Rs. 1500 between his two sons in the ratio 2 : 3. How much money does each son get?
Solution:
Let the first son get 2x and the second son get 3x.
⇒ 2x + 3x = 1500
⇒ 5x = 1500
⇒ x = \(\frac { 1500 }{ 5 } \)
⇒ x = 300
∴ first son get 2x = 2 × 300 = 600
second son get 3x = 3 × 300 = 900
Example 5: Two numbers are in the ratio 3 : 5 and their sum is 96. Find the numbers.
Solution: Let the first number be 3x and the second number be 5x.
Then, their sum = 3x + 5x = 96
8x = 96
x = 12
The first number = 3x = 3 × 12 = 36
The second number 5x = 5 × 12 = 60
Example 6: In a pencil box there are 100 pencils. Out of which 60 are red pencils and the rest are blue pencils. Find the ratio of:
(a) blue pencils to the total number of pencils.
(b) red pencils to the total number of pencils.
(c) red pencils to blue pencils.
Solution: Total number of pencils in the pencil box = 100
(a) no. of blue pencil = 100 – 60 = 40
no. of total pencil = 100
Ratio = \(\frac { 40 }{ 100 } \) =\(\frac { 4 }{ 10 } \) =\(\frac { 2 }{ 5 } \)
(b) no. of red pencil = 60
no. of blue pencil = 40
Ratio = \(\frac { 60 }{ 40 } \) =\(\frac { 6 }{ 4 } \) =\(\frac { 3 }{ 2 } \)
(c) no. of red pencil = 60
no. of total pencil = 100
Ratio = \(\frac { 60 }{ 100 } \) =\(\frac { 6 }{ 10 } \) =\(\frac { 3 }{ 5 } \)
PROPORTION
A proportion is an equation with a ratio on each side. It is a statement that two ratios are equal. When two ratios are equal then such type of equality of ratios is called proportion and their terms are said to be in proportion.
Example: If the cost of 3 pens is Rs. 21, and that of 6 pens is Rs. 42, then the ratio of pens is 3 : 6, and the ratio of their costs is 21 : 42. Thus, 3 : 6 = 21 : 42. Therefore, the terms 3, 6, 21, and 42 are in proportion.
Generally, the four terms, a, b, c, and d are in proportion if a : b = c : d.
Thus, a : b : : c : d means a/b = c/d or ad = ad = bc
Conversely, if ad = be, then a/b = c/d or a : b : : c : d
Here, a is the first term, b is the second term, c is the third term, and d is the fourth term. The first and the fourth terms are called extreme terms or extremes and the second and third terms are called middle terms or means.
Continued proportion
In a proportion, if the second and third terms are equal then the proportion is called continued proportion.
Example: If 2 : 4 : : 4 : 8, then we say that 2, 4, 8 are in continued proportion.

Mean proportion
If the terms a, b, and c are in continued proportion, then ‘b’ is called the mean proportion of a and c.
Example: If a, b, c are in continued proportion, then
Mean proportion = b2 = ac
Third proportion
If the terms a, b, c are in continued proportion, then c is called the third proportion.

Example 1: Find x, where x : 3 : : 4 : 12.
Solution: Here, x, 3, 4, and 12 are in proportion.
\(\frac { x }{ 12 } \) = \(\frac { 3 }{ 4 } \)
Now, after cross multiplying (the denominator of L.H.S. gets multiplied to the numerator of R.H.S. and similarly the denominator of R.H.S. with the numerator of L.H.S.), we get
4 × x = 3 × 12
4 × x = 36
x = \(\frac { 36 }{ 4 } \)
x = 9
So, the answer is x = 9.
Example 2: Find the third proportion of 10 and 20.
Solution: If a, b, c are in proportion, then b2 = ac.
10:20 = 20:x
\(\frac { 10 }{ 20 } \) = \(\frac { 20 }{ x } \)
20 × 20 = 10 × x
x = 40
Example 3: Find the value of x, if 14, 42, x are in continued proportion.
Solution: Here 14, 42, and x are in proportion.
The numbers is the continued proportion are in the form of \(\frac { a }{ b } \) = \(\frac { b }{ c } \)
Here, a = 14, b = 42 and c = x
Cross multiply
14 × x = 42 × 42
14 × x = 1764
∴ x = 126
∴ The value of x is 126.
Example 4: The cost of 1 dozen bananas is Rs. 24. How much do 50 bananas cost?
Solution: Let the cost of 50 bananas be x.
cost of 12 bananas =₹24
cost of 1 banana = \(\frac { 24 }{ 12 } \) = ₹2
cost of 50 bananas = (50 ×2) = ₹100
Example 5: Rajesh drives his car at a constant speed of 12 km per 10 minutes. How long will he take to cover 48 km?
Solution: Let Rajesh take x mins, to cover 48 km.
12 : 10
48 : x
⇒ 12 × x = 48 × 10
x = 40
therefore it will take Rajesh 40min to travel 48km.