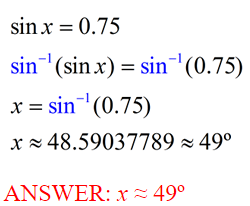Trigonometry: Solving for an Angle
Using Trigonometric Functions to Find a Missing Angle
The initial set up for solving these problems will be the same as that for finding a missing side.
To finish the problem, however, it will be necessary to use a calculator function referred to as an “inverse function” to find the actual number of degrees in the angle.
The inverse functions, on the graphing calculator, for each of the three trigonometric functions are found directly above the buttons for sine, cosine and tangent. They appear as sin-1, cos-1 and tan-1.
Note: sin-1(x) is read “the angle whose sine is x”.
You will discover, in later courses, that there are actually many angles whose sine is x, but in this course, we are looking for the simplest, most basic angle that has a sine x.
You can think of the inverse functions as “undoing” the trigonometric functions, leaving us with just the angle.
sin-1(sin x) = x
As your study of trigonometric inverse functions continues, you will see that sin-1(x), cos-1(x) and tan-1(x) may also be written as arcsin(x), arccos(x), and arctan(x), which are read “the arc whose sine is x”, and so on.
Set Up the Diagram:
Find x, to the nearest degree.
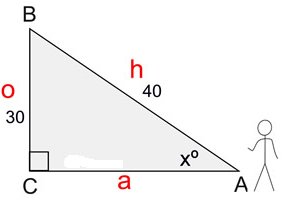
Notice that in this problem, the x is INSIDE the triangle representing the angle. The a is alone, so this problem deals with o and h, which is sine.
Set Up the Formula:
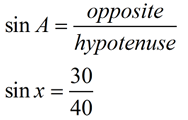
Now, divide 30 by 40 to change the fraction to a decimal.
sin x = 0.75
The goal now is to find an angle whose sine is 0.75. To do this, use the sin-1 function on your calculator!
On the graphing calculator: activate sin-1 (above the sin key) and then enter 0.75.
On the scientific calculator: enter 0.75 and then activate the sin-1 above the sin key.
Be sure you are in DEGREE MODE.