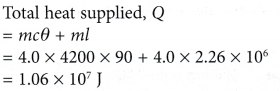Understanding Specific Latent Heat

Specific Latent Heat

The amount of heat required to change the phase of a substance depends on the mass and the type of material of the substance.
A small ice cube melts quickly but a large block of ice melts very slowly.
100 J of heat energy can melt a large amount of wax, but the same amount of heat can only melt a small amount of iron.
The specific latent heat of a substance is the amount of heat required to change the phase of 1 kg of the substance at a constant temperature.
The specific latent heat, l, of a substance can be calculated from the latent heat, Q, absorbed or released and the mass, m, of the substance that undergoes the change of phase.
where, Q = latent heat absorbed or released by the substance
m = mass of the substance
The SI unit for specific latent heat is J kg^-1.
The latent heat absorbed or released when a substance of mass m changes from one phase to another is given by:
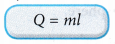
The specific latent heat of fusion of a substance is defined as the amount of heat required to change 1 kg of the substance from the solid to the liquid phase without a change in temperature.
The specific latent heat of vaporisation of a substance is defined as the amount of heat required to change 1 kg of the substance from the liquid to the gaseous phase without a change in temperature.
The specific latent heat of vaporisation of a substance is usually larger than the specific latent heat of fusion. This is due to the extra work done against atmospheric pressure during the change of phase from liquid to gas.
If heat is supplied electrically by a heater to change the phase of a substance, the formula Q = ml can be written as:
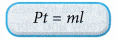where, P = power of the heater, in watts (W)
t = time the heater is switched on, in seconds (s)
Figure shows the heat and latent heat required to change a block of ice into steam. Note that the largest amount of heat is required for the change of phase from water to steam. This is due to the additional work done against atmospheric pressure when the steam expands into the air.
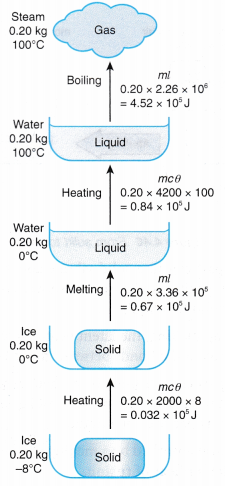
Table shows the specific latent heats of some common substances.

Understanding Specific Latent Heat 5

People also ask

What is the Latent Heat of Fusion?

The particles in a solid vibrate about their fixed mean positions. Figure shows the transition of a solid to a liquid.
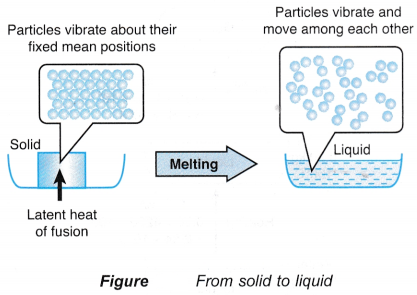
During melting, the latent heat absorbed is used to weaken the bonds between the particles.
The particles are freed from their fixed positions and are able to vibrate and move among each other as particles of a liquid.
The heat absorbed by a melting solid is known as the latent heat of fusion.
The heat required to convert a solid into the liquid state is called latent heat of fusion.
In other words ‘The latent heat of fusion of a solid is the quantity of heat in joules required to convert 1 kilogram of the solid to liquid, with out any change in temperature.
Ex: The latent heat of fusion of ice = 3.34 × 10⁵ J/kg
For a liquid to solidify at its freezing point, latent heat of fusion has to be removed from it.

What is the Latent Heat of Vaporisation?

The particles in a gas are in continuous random motion and they are much further apart from each other than the particles of a liquid.
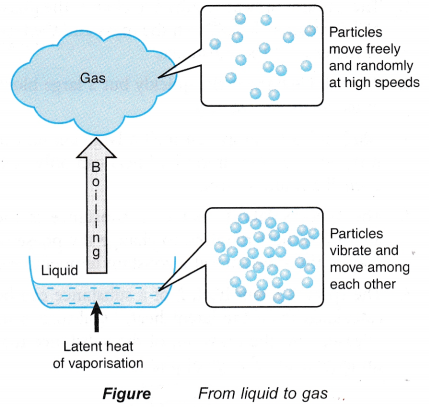
When a liquid boils, the latent heat absorbed is used to:
(a) completely break the bonds between the particles,
(b) do work against atmospheric pressure when the gaseous vapour expands into the atmosphere.
The heat absorbed during boiling is known as the latent heat of vaporisation.
The heat required to convert a liquid into the vapour state is called latent heat of vaporisation.
The other words ‘The latent heat of vaporisation of a liquid is the quantity of heat in joules required to convert 1 kilogram of the liquid to vapour or gas, without any change in temperature.
Ex: Latent heat of vaporisation of water = 22.5 × 10⁵ J/kg
When vapour condenses back into a liquid, latent heat of vaporisation is released.

Latent Heat of Fusion of Ice Experiment

Aim: To determine the specific latent heat of fusion of ice.
Material: Crushed ice
Apparatus: Two immersion heaters, two filter funnels, stopwatch
Method:
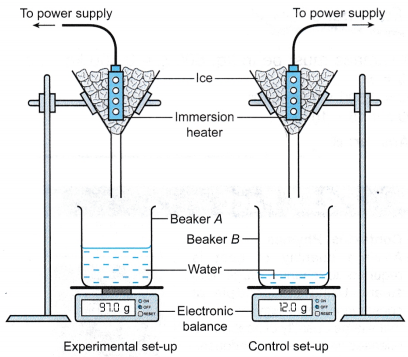
Specific Latent Heat Experiment

Beaker A and beaker B are placed on their respective electronic balances. The readings of the electronic balances are reset to zero.
The apparatus is set up as shown in Figure. Initially the filter funnels are not placed over the beakers.
The heater for experimental set-up is switched on. When water is dripping out of the filter funnels at a constant rate, the filter funnels are placed over Beaker A and Beaker B respectively, and a stopwatch is started.
After 10 minutes, the mass of water collected in beaker A and beaker B are measured and recorded as m₁ and m₂respectively.
The power of the immersion heater, P, is recorded.

Results:
Specific Latent Heat Experiment 1
Analysis of Data:
Mass of ice melted by the heat supplied from the heater,
m = (m₁ – m₂) g
= (97.0 – 12.0) g = 85.0 g
= 0.085 kg
Heat supplied, Q = Pt
= 48 x 10 x 60 J = 28 800 J

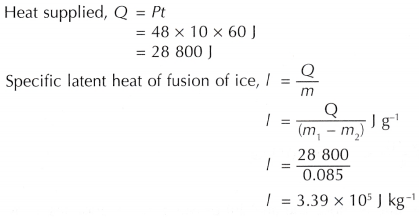
Discussion:

The temperature of ice is lower than the room temperature. The ice will absorb heat from the surroundings and melt by itself. The control set of apparatus was set up to determine the mass of ice that was melted by the heat from the surroundings. Only then, the correct mass of ice melted by the heater can be determined.
Crushed ice was used because the large surface area of the crushed ice allows for a more efficient absorption of heat.
The value of the specific latent heat of fusion of ice obtained from this activity is larger than the standard value. Some of the heat supplied by the heater is lost to the surroundings. In the calculation, it was assumed that no heat was lost to the surroundings and all the heat supplied was absorbed by the ice only.

Conclusion:
The specific latent heat of fusion of ice determined by the activity is 3.39 x 105 J kg^-1.

Latent Heat of Vaporisation of Water Experiment

Aim: To determine the specific latent heat of vaporisation of water. Material: Tap water
Apparatus: Immersion heater, beaker, electronic balance, stopwatch
Method:
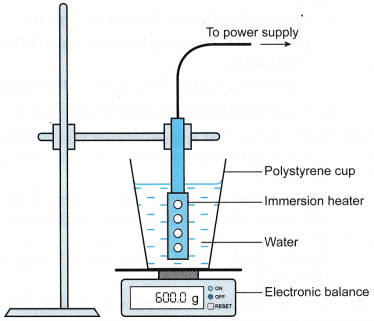
Specific Latent Heat Experiment 3

The apparatus is set up as shown in Figure.
The heater is turned on to boil the water.
When the water is boiling steadily, the stopwatch is started. At the same time, the reading on the electronic balance is recorded as m₁
After a time, t = 10 minutes, the reading on the electronic balance is recorded as m₂.
The heater is switched off. The power of the heater, P is recorded.

Results:
Specific Latent Heat Experiment 4
Analysis of Data:

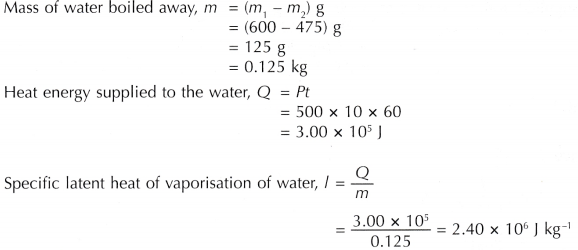
Discussion:

A high powered heater is used so that the boiling time is short. The amount of water that evaporates away during the short time of the experiment is very small and can be neglected. Therefore, a control set of apparatus is not necessary-for this activity.
The value of the specific latent heat of vaporisation of water obtained from this activity is larger than the standard value. Some of the heat supplied by the heater is lost to the surroundings. In the calculation, it was assumed that no heat was lost to the surroundings and all the heat supplied was absorbed by the water only.

Conclusion:
The specific latent heat of vaporisation of water determined by the activity is 2.40 x 106 J kg^-1.

Specific Latent Heat Example Problems With Solutions

A plastic bag containing 0.80 kg of soup at 38°C is put into the freezer compartment of a refrigerator. Calculate the amount of heat that must be removed to completely solidify the soup.
Assume the soup solidifies at -2°C.
[Specific heat capacity of the soup c = 4250 J kg^-1 °C^-1; specific latent heat of fusion of the soup, l = 3.38 x 10⁵ J kg^-1]
Solution:
The changes from liquid soup to solid can illustrated in the following diagram.
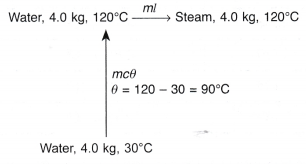
In a boiler, water boils at 120°C. How much heat must be supplied to 4.0 kg of water at 30°C to change it to steam at the same temperature?
[Specific heat capacity, c = 4200 J kg^-1 °C^-1; specific latent heat of vaporisation, l = 2.26 x 10⁶ J kg^-1]
Solution: