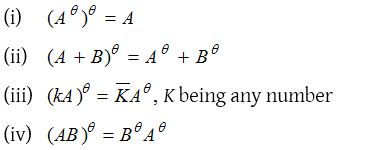What are the Special Types of Matrices?
Singular and Non-singular matrix :
Any square matrix A is said to be non-singular if |A| ≠ 0, and a square matrix A is said to be singular if |A| = 0. Here |A| (or det(A) or simply det |A| means corresponding determinant of square matrix A.
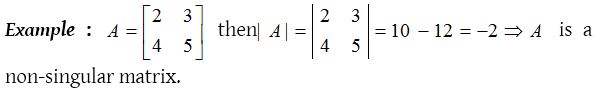
Hermitian and Skew-hermitian matrix :
A square matrix is said to be hermitian matrix if
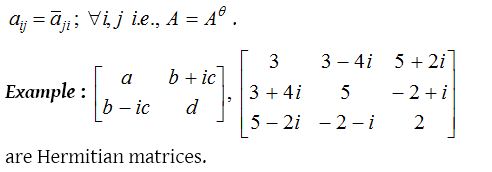
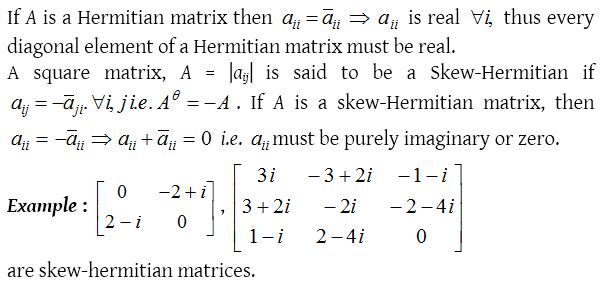
Orthogonal matrix :
A square matrix A is called orthogonal if AAT = I = AT A i.e., if A−1 = A.
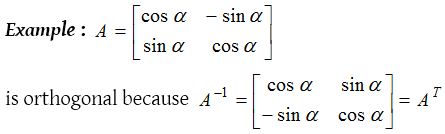
In fact every unit matrix is orthogonal. Determinant of orthonogal matrix is – 1 or 1.
Idempotent matrix :
A square matrix A is called an idempotent matrix if A2 = A.
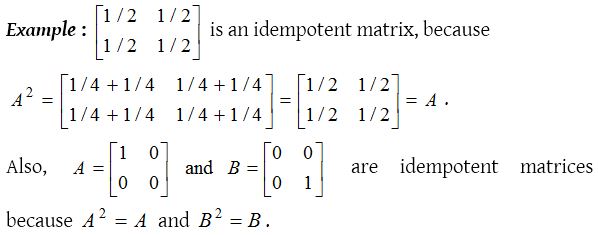
In fact every unit matrix is indempotent.
Involutory matrix :
A square matrix A is called an involutory matrix if A2 = I or A−1 = A.
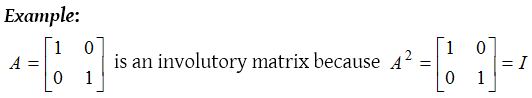
In fact every unit matrix is involutory.
Nilpotent matrix :
A square matrix A is called a nilpotent matrix if there exists a p ∈ N such that Ap = 0.
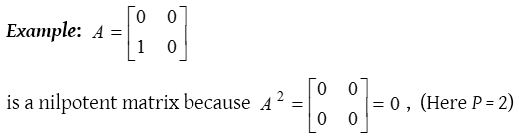
Determinant of every nilpotent matrix is 0.

Periodic matrix :
A matrix A will be called a periodic matrix if where k is a positive integer. If Ak+1 = A however k is the least positive integer for Ak+1 = A, then k is said to be the period of A.
Differentiation of a matrix : If then is a differentiation of matrix A.
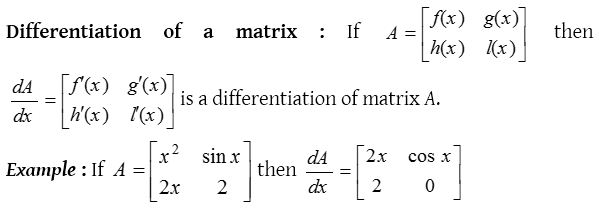
Conjugate of a matrix :
The matrix obtained from any given matrix A containing complex number as its elements, on replacing its elements by the corresponding conjugate complex numbers is called conjugate of A and is denoted by \(\overline { A }\).
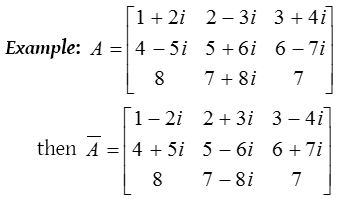
Properties of conjugates

Transpose conjugate of a matrix :
The transpose of the conjugate of a matrix A is called transposed conjugate of A and is denoted by Aθ. The conjugate of the transpose of A is the same as the transpose of the conjugate of A
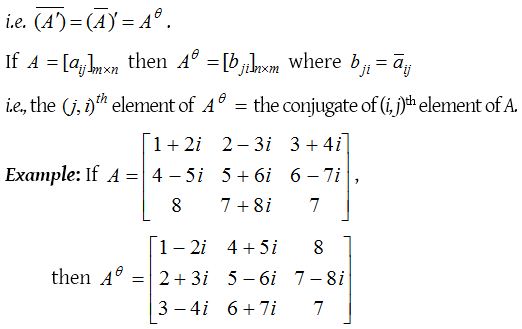
Properties of transpose conjugate