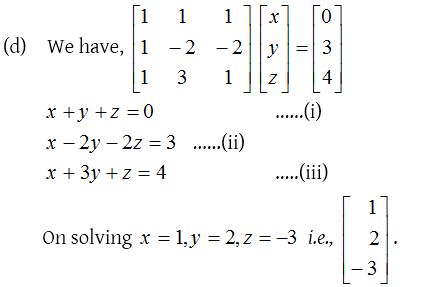Solving Systems of Linear Equations Using Matrices
Homogeneous and non-homogeneous systems of linear equations
A system of equations AX = B is called a homogeneous system if B = O. If B ≠ O, it is called a non-homogeneous system of equations.
e.g., 2x + 5y = 0
3x – 2y = 0
is a homogeneous system of linear equations whereas the system of equations given by
e.g., 2x + 3y = 5
x + y = 2
is a non-homogeneous system of linear equations.
Solution of Non-homogeneous system of linear equations
- Matrix method: If AX = B, then X = A-1B gives a unique solution, provided A is non-singular.
But if A is a singular matrix i.e., if |A| = 0, then the system of equation AX = B may be consistent with infinitely many solutions or it may be inconsistent. - Rank method for solution of Non-Homogeneous system AX = B
- Write down A, B
- Write the augmented matrix [A : B]
- Reduce the augmented matrix to Echelon form by using elementary row operations.
- Find the number of non-zero rows in A and [A : B] to find the ranks of A and [A : B] respectively.
- If ρ(A) ≠ ρ(A : B) then the system is inconsistent.
- ρ(A) = ρ(A : B) = the number of unknowns, then the system has a unique solution.
- ρ(A) = ρ(A : B) < number of unknowns, then the system has an infinite number of solutions.
Solutions of a homogeneous system of linear equations
Let AX = O be a homogeneous system of 3 linear equations in 3 unknowns.
- Write the given system of equations in the form AX = O and write A.
- Find |A|.
- If |A| ≠ 0, then the system is consistent and x = y = z = 0 is the unique solution.
- If |A| = 0, then the systems of equations has infinitely many solutions. In order to find that put z = k (any real number) and solve any two equations for x and y so obtained with z = k give a solution of the given system of equations.
Consistency of a system of linear equation AX = B, where A is a square matrix
In system of linear equations AX = B, A = (aij)n×n is said to be
- Consistent (with unique solution) if |A| ≠ 0.
i.e., if A is non-singular matrix. - Inconsistent (It has no solution) if |A| = 0 and (adj A)B is a non-null matrix.
- Consistent (with infinitely m any solutions) if |A| = 0 and (adj A)B is a null matrix.
Rank of matrix
Definition:
Let A be a m×n matrix. If we retain any r rows and r columns of A we shall have a square sub-matrix of order r. The determinant of the square sub-matrix of order r is called a minor of A order r. Consider any matrix A which is of the order of 3×4 say,
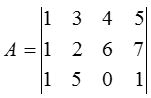 .
.
It is 3×4 matrix so we can have minors of order 3, 2 or 1. Taking any three rows and three columns minor of order three. Hence minor of order \(3=\left| \begin{matrix} 1 & 3 & 4 \\ 1 & 2 & 6 \\ 1 & 5 & 0 \end{matrix} \right| =0\)
Making two zeros and expanding above minor is zero. Similarly we can consider any other minor of order 3 and it can be shown to be zero. Minor of order 2 is obtained by taking any two rows and any two columns.
Minor of order \(2=\begin{vmatrix} 1 & 3 \\ 1 & 2 \end{vmatrix}=2-3=-1\neq 0\).
Minor of order 1 is every element of the matrix.
Rank of a matrix: The rank of a given matrix A is said to be r if
- Every minor of A of order r+1 is zero.
- There is at least one minor of A of order r which does not vanish. Here we can also say that the rank of a matrix A is said to be r ,if
- Every square submatrix of order r+1 is singular.
- There is at least one square submatrix of order r which is non-singular.
The rank r of matrix A is written as ρ(A) = r.
Echelon form of a matrix
A matrix A is said to be in Echelon form if either A is the null matrix or A satisfies the following conditions:
- Every non- zero row in A precedes every zero row.
- The number of zeros before the first non-zero element in a row is less than the number of such zeros in the next row.
If can be easily proved that the rank of a matrix in Echelon form is equal to the number of non-zero row of the matrix.
Rank of a matrix in Echelon form: The rank of a matrix in Echelon form is equal to the number of non-zero rows in that matrix.
Solving Systems of Linear Equations Using Matrices Problems with Solutions
1.
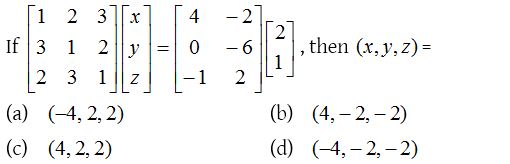
Solution:
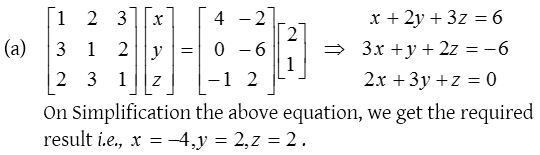
2.
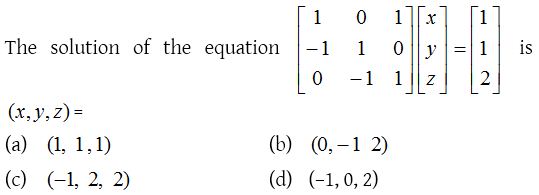
Solution:

3.
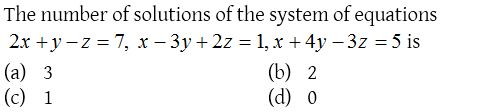
Solution:
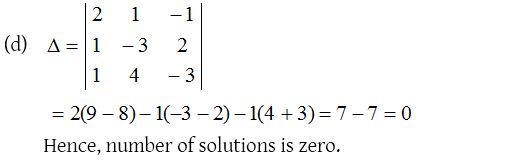
4.

Solution:

5.
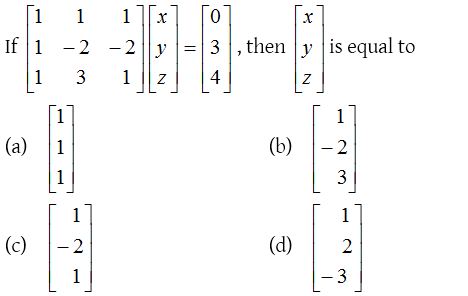
Solution: