Selina Concise Mathematics Class 10 ICSE Solutions Quadratic Equations

Selina Concise Mathematics Class 10 ICSE Solutions Quadratic Equations

Selina Publishers Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations

Quadratic Equations Exercise 5A – Selina Concise Mathematics Class 10 ICSE Solutions

Find which of the following equations are quadratic:

Solution 1(i)
(3x – 1)² = 5(x + 8)
⇒ (9x² – 6x + 1) = 5x + 40
⇒ 9x² – 11x – 39 =0; which is of the form ax² + bx + c = 0.
∴ Given equation is a quadratic equation.

Solution 1(ii)
5x² – 8x = -3(7 – 2x)
⇒ 5x² – 8x = 6x – 21
⇒ 5x² – 14x + 21 =0; which is of the form ax² + bx + c = 0.
∴ Given equation is a quadratic equation.

Solution 1(iii)
(x – 4)(3x + 1) = (3x – 1)(x +2)
⇒ 3x² + x – 12x – 4 = 3x² + 6x – x – 2
⇒ 16x + 2 =0; which is not of the form ax² + bx + c = 0.
∴ Given equation is not a quadratic equation.

Solution 1(iv)
x² + 5x – 5 = (x – 3)²
⇒ x² + 5x – 5 = x² – 6x + 9
⇒ 11x – 14 =0; which is not of the form ax² + bx + c = 0.
∴ Given equation is not a quadratic equation.

Solution 1(v)
7x³ – 2x² + 10 = (2x – 5)²
⇒ 7x³ – 2x² + 10 = 4x² – 20x + 25
⇒ 7x³ – 6x² + 20x – 15 = 0; which is not of the form ax² + bx + c = 0.
∴ Given equation is not a quadratic equation.

Solution 1(vi)
(x – 1)² + (x + 2)² + 3(x +1) = 0
⇒ x² – 2x + 1 + x² + 4x + 4 + 3x + 3 = 0
⇒ 2x² + 5x + 8 = 0; which is of the form ax² + bx + c = 0.
∴ Given equation is a quadratic equation.

Question 2(i)
Is x = 5 a solution of the quadratic equation x² – 2x – 15 = 0?
Solution:
x² – 2x – 15 = 0
For x = 5 to be solution of the given quadratic equation it should satisfy the equation.
So, substituting x = 5 in the given equation, we get
L.H.S = (5)² – 2(5) – 15
= 25 – 10 – 15
= 0
= R.H.S
Hence, x = 5 is a solution of the quadratic equation x² – 2x – 15 = 0.

Question 2(ii).
Is x = -3 a solution of the quadratic equation 2x² – 7x + 9 = 0?
Solution:
2x² – 7x + 9 = 0
For x = -3 to be solution of the given quadratic equation it should satisfy the equation
So, substituting x = 5 in the given equation, we get
L.H.S =2(-3)² – 7(-3) + 9
= 18 + 21 + 9
= 48
≠ R.H.S
Hence, x = -3 is not a solution of the quadratic equation 2x² – 7x + 9 = 0.

Question 3.
If \(\sqrt{\frac{2}{3}}\) is a solution of equation 3x² + mx + 2 = 0, find the value of m.
Solution:
For x = \(\sqrt{\frac{2}{3}}\) to be solution of the given quadratic equation it should satisfy the equation
So, substituting x = \(\sqrt{\frac{2}{3}}\) in the given equation, we get

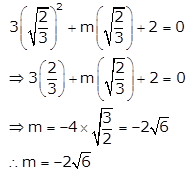
Question 4.
\(\frac{2}{3}\) and 1 are the solutions of equation mx² + nx + 6 = 0. Find the values of m and n.
Solution:
For x =  \(\frac{2}{3}\) and x = 1 to be solutions of the given quadratic equation it should satisfy the equation
So, substituting x =  \(\frac{2}{3}\) and x = 1 in the given equation, we get

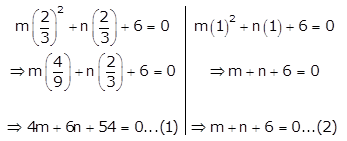
Solving equations (1) and (2) simultaneously,
4m  + 6n + 54 = 0 …..(1)
m + n  + 6 = 0 ….(2)
(1) – (2) × 6
⇒ -2m + 18 = 0
⇒ m = 9
Substitute in (2)
⇒ n = -15

Question 5.
If 3 and -3 are the solutions of equation ax² + bx – 9 = 0. Find the values of a and b.
Solution:
For x = 3 and x = -3 to be solutions of the given quadratic equation it should satisfy the equation
So, substituting x = 3 and x = -3 in the given equation, we get

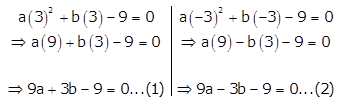
Solving equations (1) and (2) simultaneously,
9a + 3b – 9 = 0 …(1)
9a – 3b – 9 = 0 …(2)
(1) + (2)
⇒ 18a – 18 = 0
⇒ a = 1
Substitute in (2)
⇒ b = 0

Quadratic Equations Exercise 5B – Selina Concise Mathematics Class 10 ICSE Solutions

Question 1.
Without solving, comment upon the nature of roots of each of the following equations :
(i) 7x² – 9x +2 =0
(ii) 6x² – 13x +4 =0
(iii) 25x² – 10x +1=0
(iv) x² + 2√3x – 9=0
(v) x² – ax – b² =0
(vi) 2x² +8x +9=0
Solution:

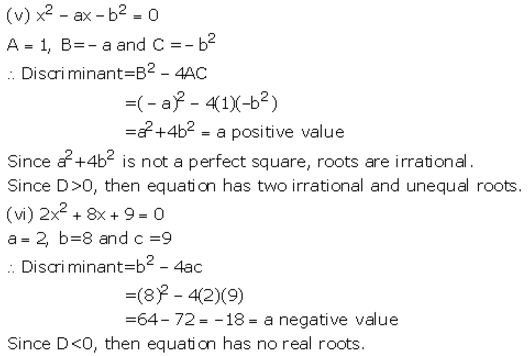
Question 2.
Find the value of p, if the following quadratic equation has equal roots : 4x² – (p – 2)x + 1 = 0
Solution:

Question 3.
Find the value of ‘p’, if the following quadratic equations have equal roots : x² + (p – 3)x + p = 0
Solution:
x² + (p – 3)x + p = 0
Here, a = 1, b = (p – 3), c = p
Since, the roots are equal,
⇒ b²– 4ac = 0
⇒ (p – 3)²– 4(1)(p) = 0
⇒p² + 9 – 6p – 4p = 0
⇒ p²– 10p + 9 = 0
⇒p²-9p – p + 9 = 0
⇒p(p – 9) – 1(p – 9) = 0
⇒ (p -9)(p – 1) = 0
⇒ p – 9 = 0 or p – 1 = 0
⇒ p = 9 or p = 1

Question 4.
The equation 3x² – 12x + (n – 5)=0 has equal roots. Find the value of n.
Solution:

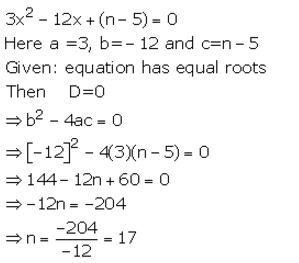
Question 5.
Find the value of m, if the following equation has equal roots : (m – 2)x² – (5+m)x +16 =0
Solution:

Question 6.
Find the value of p for which the equation 3x²– 6x + k = 0 has distinct and real roots.
Solution:

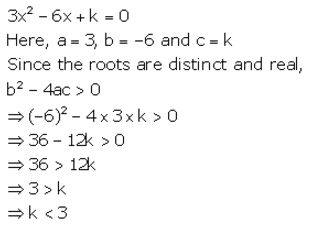
Quadratic Equations Exercise 5C – Selina Concise Mathematics Class 10 ICSE Solutions

Question 1.
Solve : x² – 10x – 24 = 0
Solution:

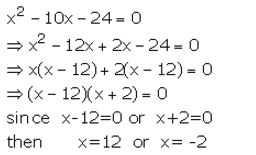
Question 2.
Solve : x² – 16 = 0
Solution:

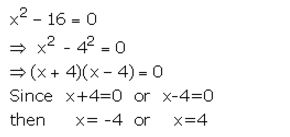
Question 3.

Solution:

Question 4.
Solve : x(x – 5) = 24
Solution:

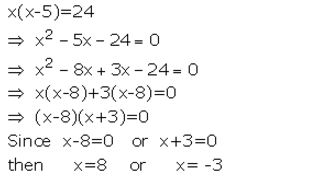
Question 5.

Solution:

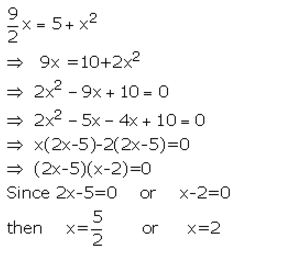
Question 6.

Solution:

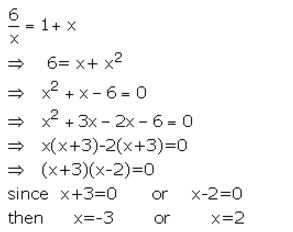
Question 7.

Solution:

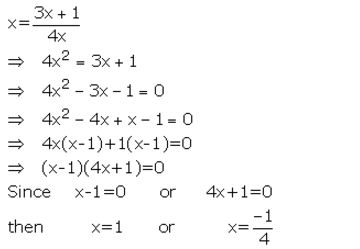
Question 8.

Solution:

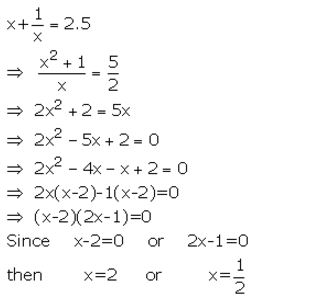
Question 9.
Solve : (2x – 3)² = 49
Solution:

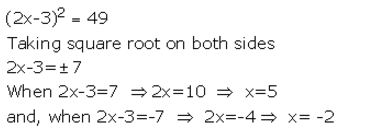
Question 10.
Solve : 2(x² – 6) = 3(x – 4)
Solution:

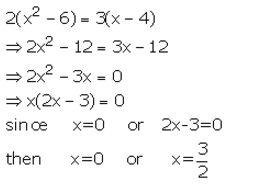
Question 11.
Solve : (x + 1)(2x + 8) = (x + 7)(x + 3)
Solution:

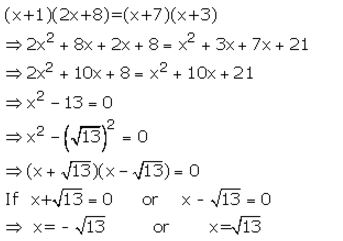
Question 12.
Solve : x² – (a + b)x + ab = 0
Solution:

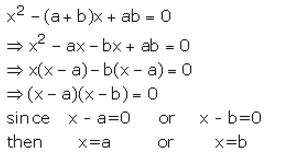
Question 13.
(x + 3)² – 4(x + 3) – 5 = 0
Solution:

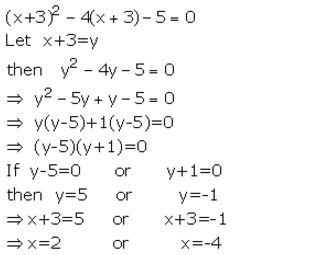
Question 14.
4(2x – 3)² – (2x – 3) – 14 = 0
Solution:

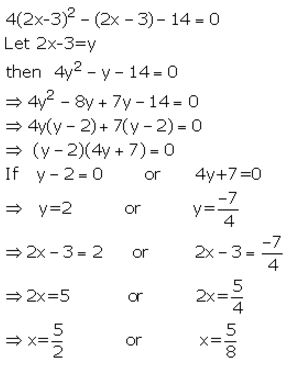
Question 15.

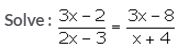
Solution:

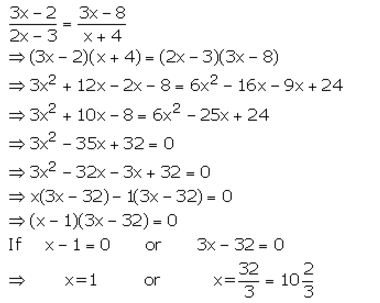
Question 16.
2x² – 9x + 10 = 0, When
(i) x∈ N
(ii) x∈ Q
Solution:

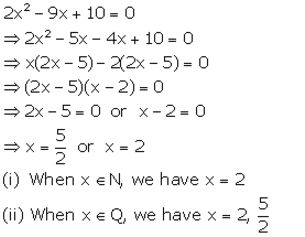
Question 17.

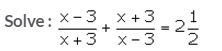
Solution:

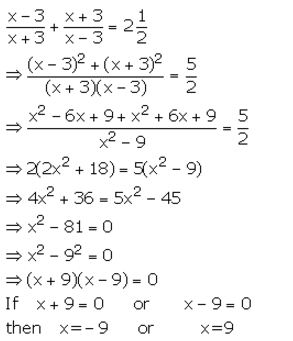
Question 18.

Solution:

Question 19.

Solution:

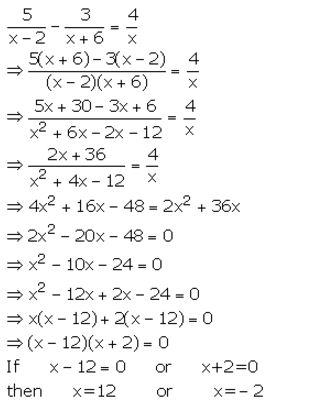
Question 20.

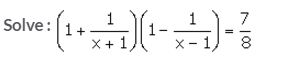
Solution:

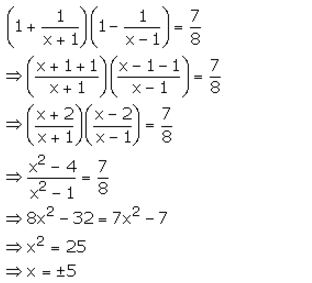
Question 21.
Find the quadratic equation, whose solution set is :
(i) {3, 5} (ii) {-2, 3}
Solution:

Question 22.

Solution:

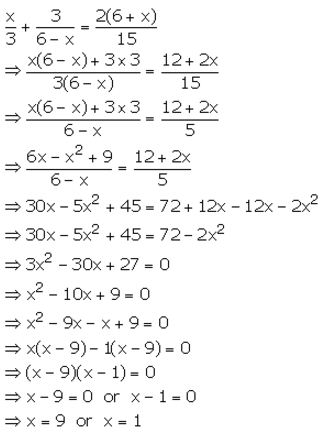
Question 23.

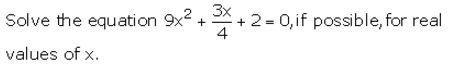
Solution:

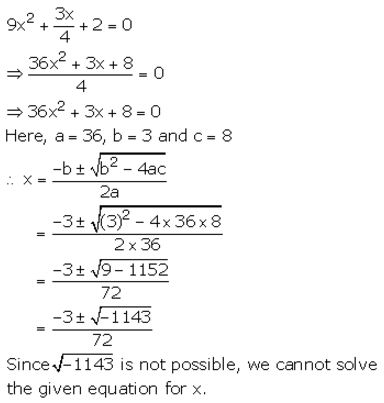
Question 24.
Find the value of x, if a + 1=0 and x² + ax – 6 =0.
Solution:

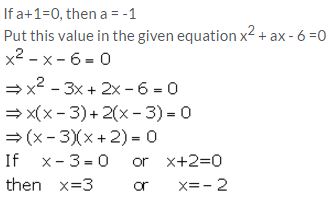
Question 25.
Find the value of x, if a + 7=0; b + 10=0 and 12x² = ax – b.
Solution:
If a + 7 =0, then a = -7
and b + 10 =0, then b = – 10
Put these values of a and b in the given equation

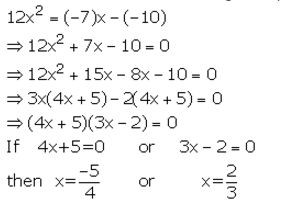
Question 26.
Use the substitution y= 2x +3 to solve for x, if 4(2x+3)² – (2x+3) – 14 =0.
Solution:

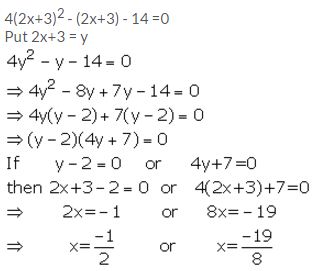
Question 27.
Without solving the quadratic equation 6x² – x – 2=0, find whether x = 2/3 is a solution of this equation or not.
Solution:

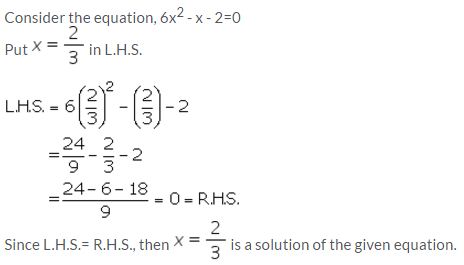
Question 28.
Determine whether x = -1 is a root of the equation x² – 3x +2=0 or not.
Solution:
x² – 3x +2=0
Put x = -1 in L.H.S.
L.H.S. = (-1)² – 3(-1) +2
= 1 +3 +2=6 ≠ R.H.S
Then x = -1 is not the solution of the given equation.

Question 29.
If x = 2/3 is a solution of the quadratic equation 7x²+mx – 3=0; Find the value of m.
Solution:

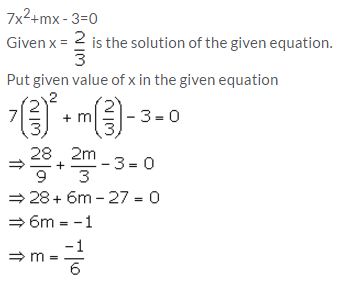
Question 30.
If x = -3 and x = 2/3 are solutions of quadratic equation mx² + 7x + n = 0, find the values of m and n.
Solution:

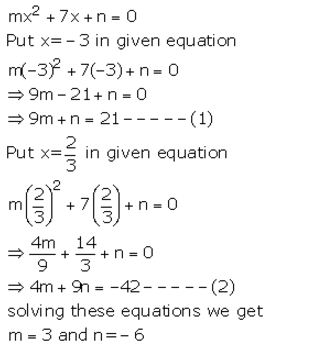
Question 31.
If quadratic equation x² – (m + 1) x + 6=0 has one root as x =3; find the value of m and the root of the equation.
Solution:

Question 32.
Given that 2 is a root of the equation 3x² – p(x + 1) = 0 and that the equation px² – qx + 9 = 0 has equal roots, find the values of p and q.
Solution:

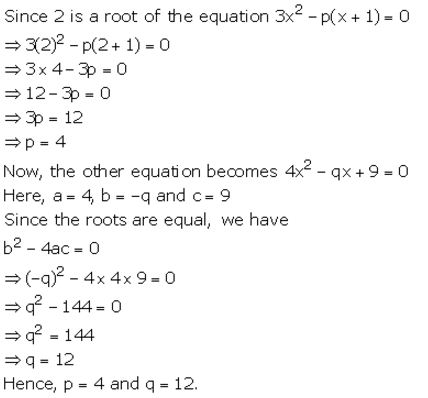
Question 33.

Solution:

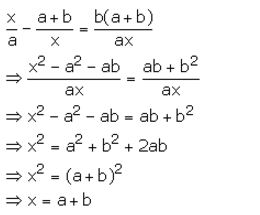
Question 34.

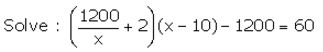
Solution:

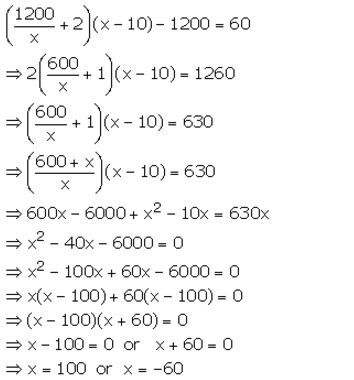
Question 35.
If -1 and 3 are the roots of x² + px + q = 0, find the values of p and q.
Solution:

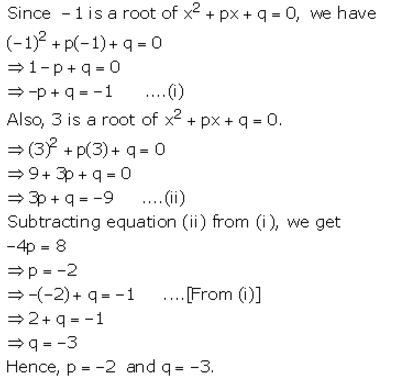
Quadratic Equations Exercise 5D – Selina Concise Mathematics Class 10 ICSE Solutions

Question 1.

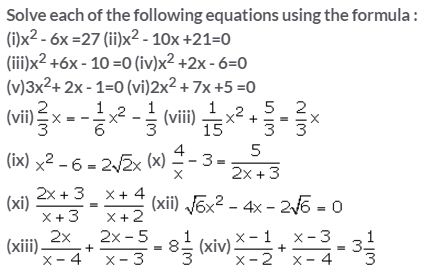
Solution:

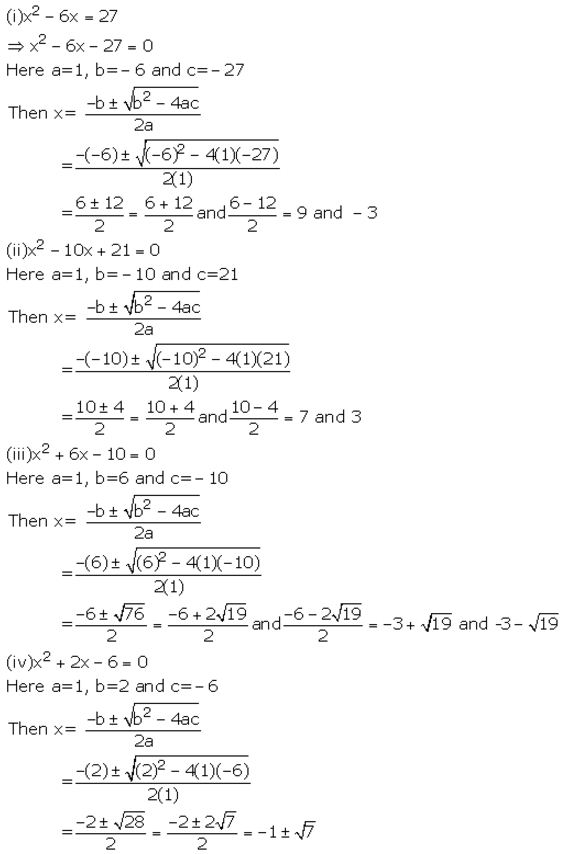
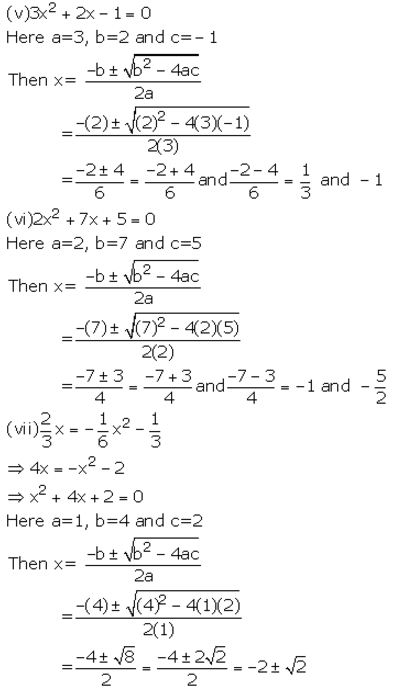
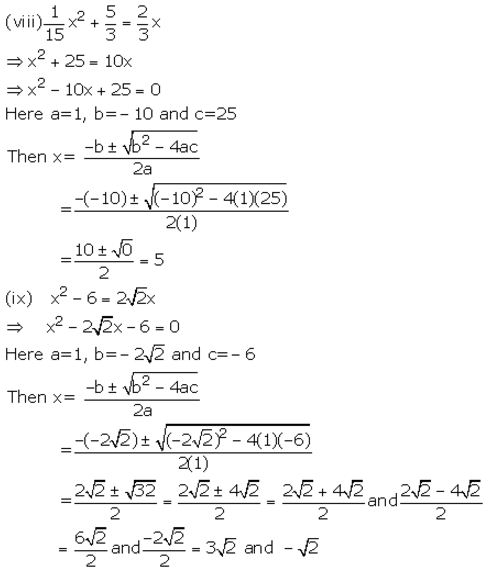
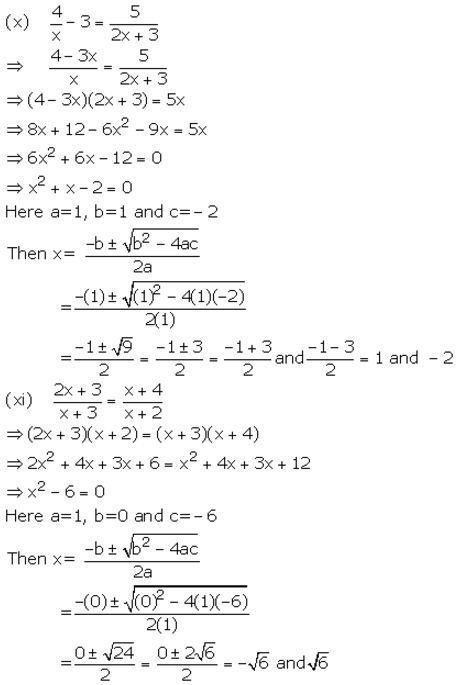
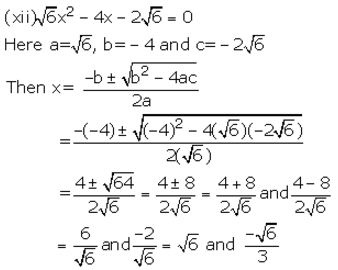
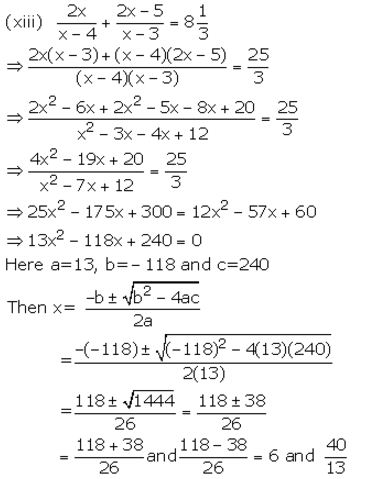
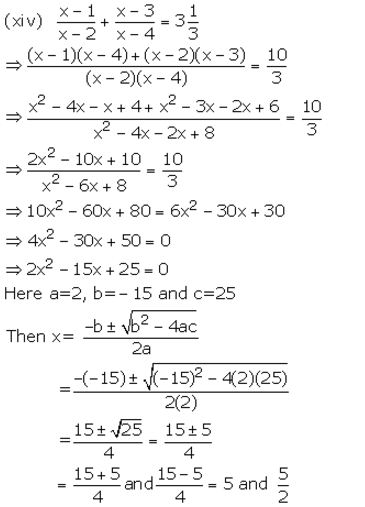
Question 2.
Solve each of the following equations for x and give, in each case, your answer correct to one decimal place :
(i) x² – 8x+5=0
(ii) 5x² +10x – 3 =0
Solution:

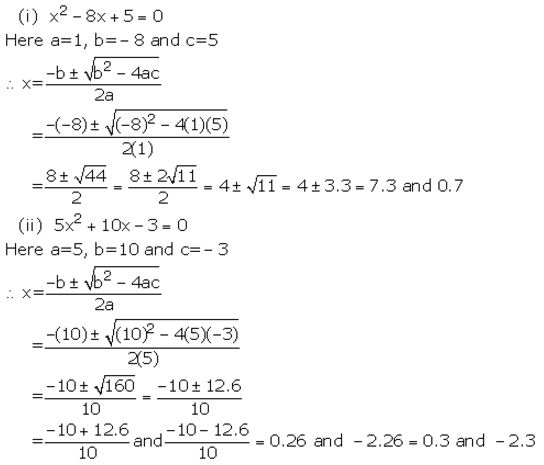
Question 3(i).
Solve each of the following equations for x and give, in each case, your answer correct to two decimal places :
(i) 2x² – 10x +5=0
Solution:

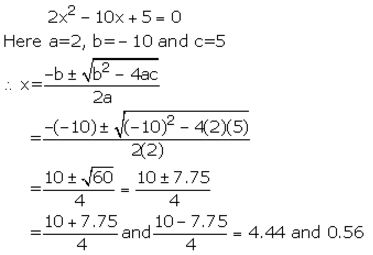
Question 3(ii).
Solve each of the following equations for x and give, in each case, your answer correct to two decimal places :
4x + 6/x + 13 = 0
Solution:

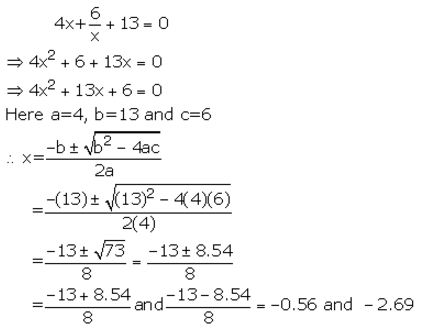
Question 3(iii).
Solve each of the following equations for x and give, in each case, your answer correct to two decimal places :
x² – 3x – 9 =0
Solution:

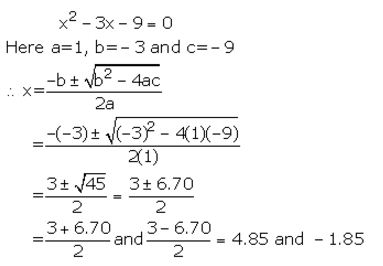
Question 3(iv).
Solve each of the following equations for x and give, in each case, your answer correct to two decimal places :
x² – 5x – 10 = 0
Solution:

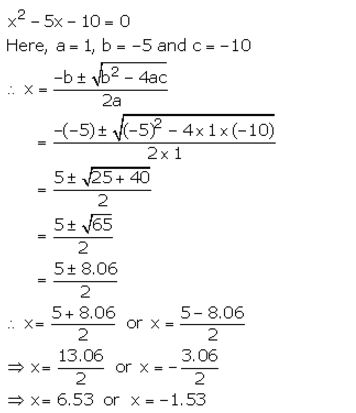
Question 4.
Solve each of the following equations for x and give, in each case, your answer correct to 3 decimal places :
(i) 3x² – 12x – 1 =0
(ii) x² – 16 x +6= 0
(iii) 2x² + 11x + 4= 0
Solution:

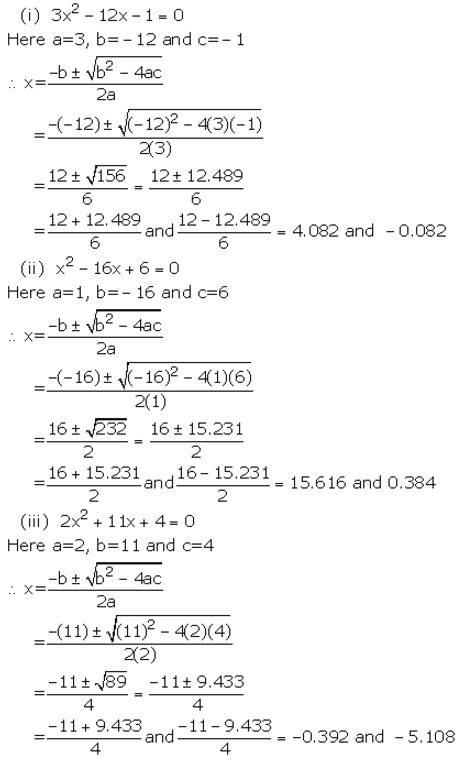
Question 5.
Solve:
(i) x⁴ – 2x² – 3 =0
(ii) x⁴ – 10x² +9 =0
Solution:

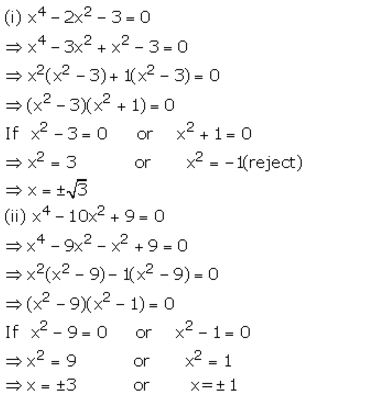
Question 6.
Solve :
(i) (x² – x)² + 5(x² – x)+ 4=0
(ii) (x² – 3x)² – 16(x² – 3x) – 36 =0
Solution:

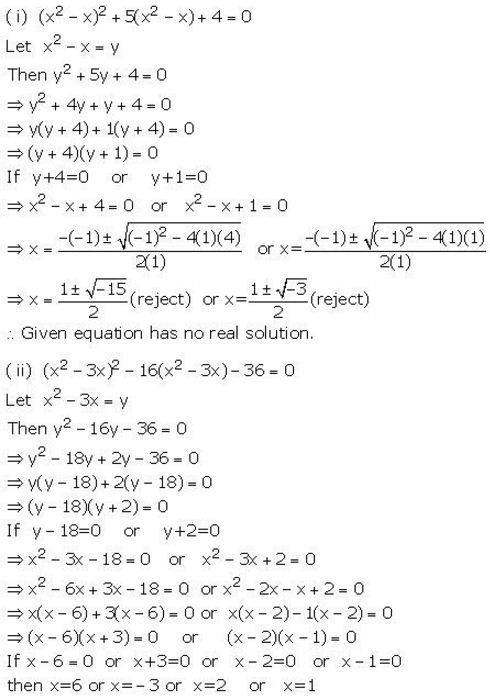
Question 7.

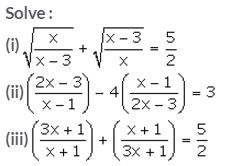
Solution:

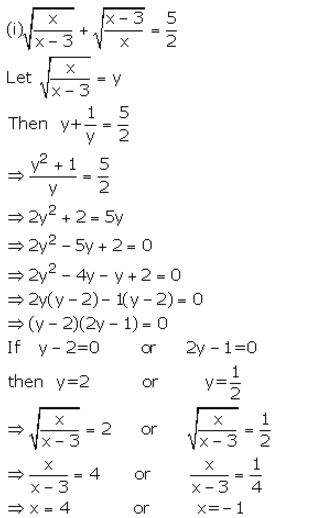
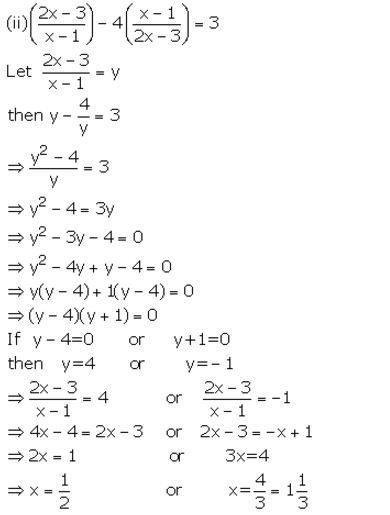
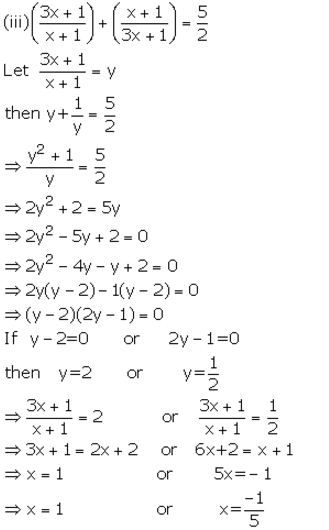
Question 8.

Solution:

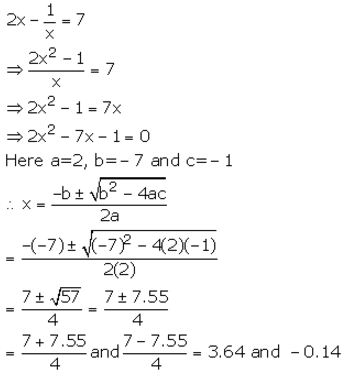
Question 9.
Solve the following equation and give your answer correct to 3 significant figures:
5x² – 3x – 4 = 0
Solution:

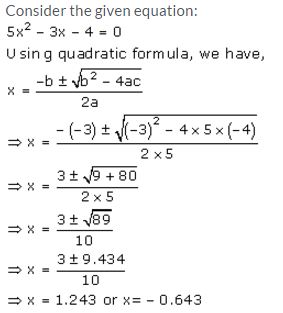
Question 10.
Solve for x using the quadratic formula. Write your answer correct to two significant figures.
(x – 1)² – 3x + 4 = 0
Solution:

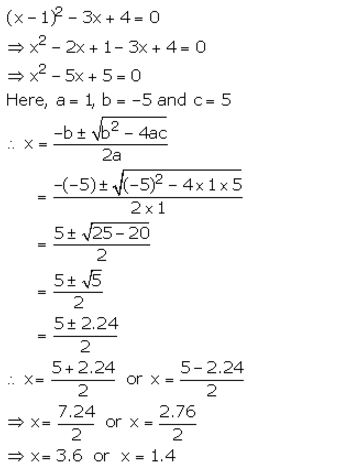
Question 11.
Solve the quadratic equation x² – 3 (x+3) = 0; Give your answer correct to two significant figures.
Solution:

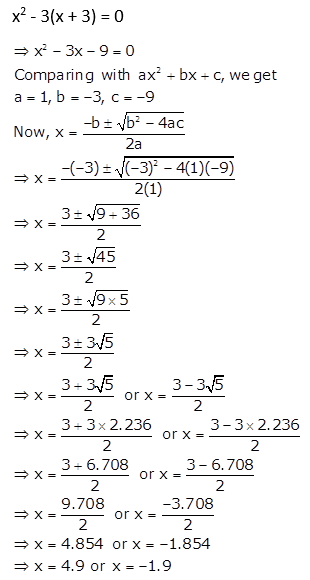
Quadratic Equations Exercise 5E – Selina Concise Mathematics Class 10 ICSE Solutions

Question 1.

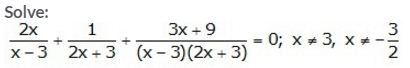
Solution:

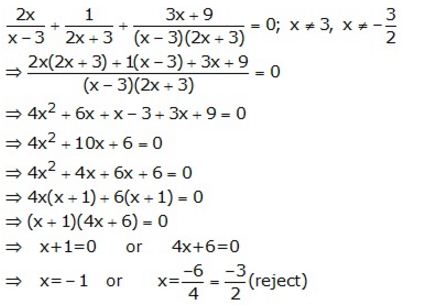
Question 2.
Solve: (2x+3)²=81
Solution:

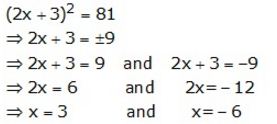
Question 3.
Solve: a²x² – b² = 0
Solution:

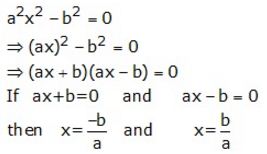
Question 4.

Solution:

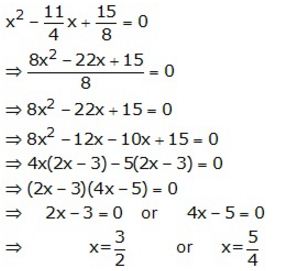
Question 5.

Solution:

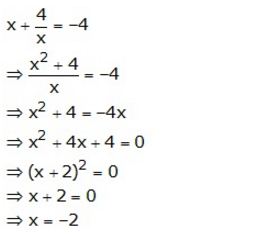
Question 6.
Solve: 2x⁴ – 5x² + 3 = 0
Solution:

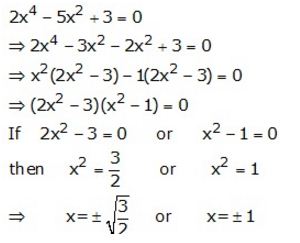
Question 7.
Solve: x⁴ – 2x² – 3 = 0.
Solution:

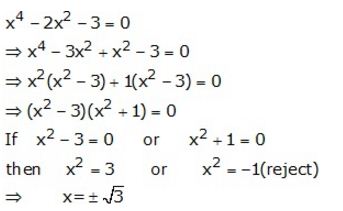
Question 8.

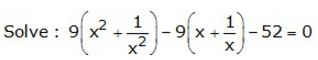
Solution:

Question 9.

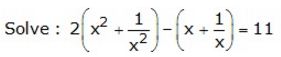
Solution:

Question 10.

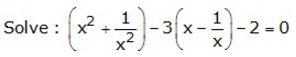
Solution:

Question 11.
Solve : (x² + 5x + 4)(x² + 5x + 6) = 120
Solution:

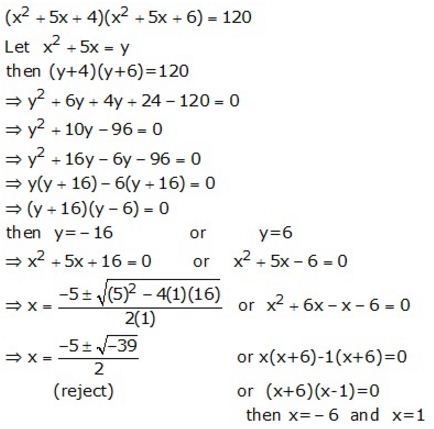
Question 12.
Solve each of the following equations, giving answer upto two decimal places.
(i) x² – 5x -10=0 (ii) 3x² – x – 7 =0
Solution:

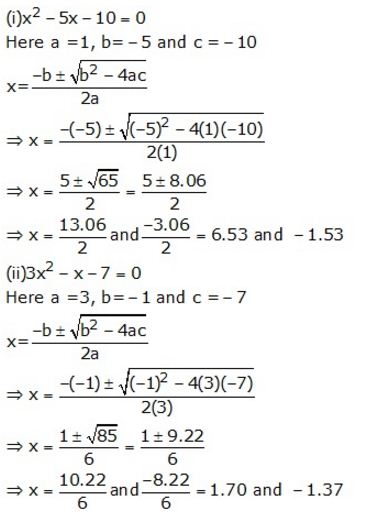
Question 13.

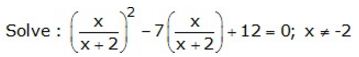
Solution:

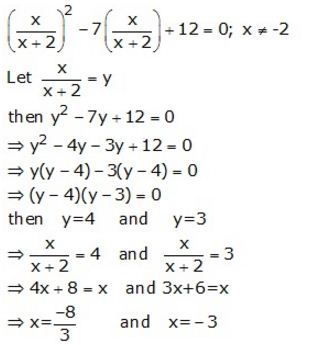
Question 14.
Solve :
(i) x² – 11x – 12 =0; when x ∈ N
(ii) x² – 4x – 12 =0; when x ∈ I
(iii) 2x² – 9x + 10 =0; when x ∈ Q
Solution:

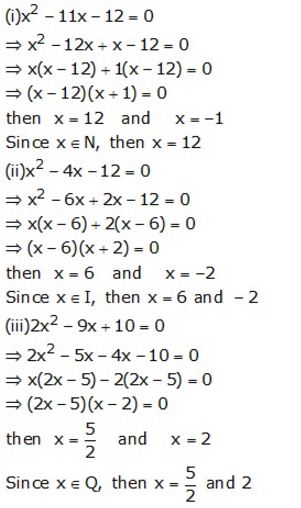
Question 15.
Solve : (a + b)²x² – (a + b)x – 6 = 0; a + b ≠ 0
Solution:

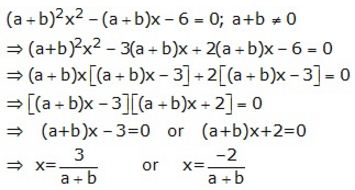
Question 16.

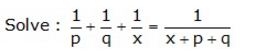
Solution:

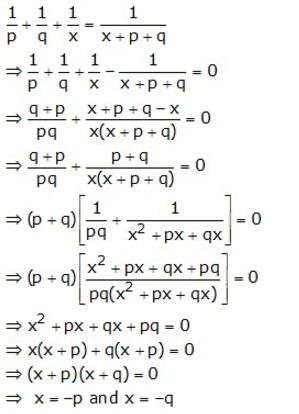
Question 17.

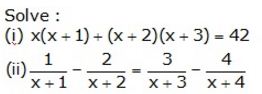
Solution:

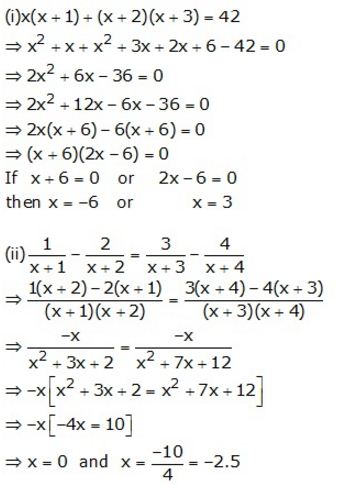
Question 18.

Solution:

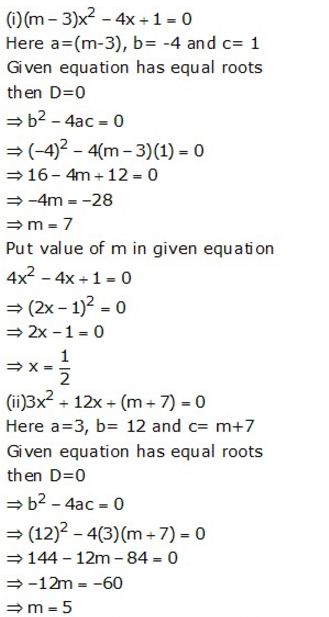
Question 19.

Solution:

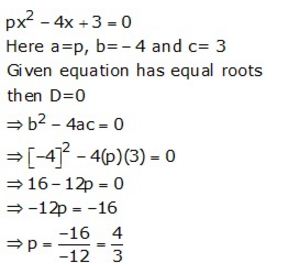
Question 20.
Without solving the following quadratic equation, find the value of ‘m’ for which the given equation has real and equal roots.
x² + 2(m – 1)x + (m + 5) = 0
Solution:

Quadratic Equations Exercise 5F – Selina Concise Mathematics Class 10 ICSE Solutions

Solution 1(i)
Given: (x + 5)(x – 5)=24
⇒ x² – 5² = 24   …. since (a – b)(a + b) = a² – b²
⇒ x² – 25 = 24
⇒ x² = 49
⇒ x = ± 7

Solution 1(ii)
Given: 3x² – 2\(\sqrt{6}\)x + 2 = 0

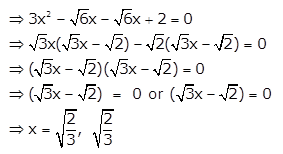
Solution 1(iii)
Given: 3\(\sqrt{2}\)x² – 5x – \(\sqrt{26}\) = 0

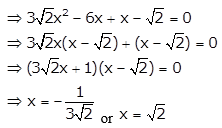
Question 2.
One root of the quadratic equation 8x² + mx + 15 is 3/4. Find the value of m. Also, find the other root of the equation.
Solution:
Given quadratic equation is  8x² + mx + 15 = 0   …. (i)
One of the roots of (i) is \(\frac{3}{4}\), so it satisfies (i)

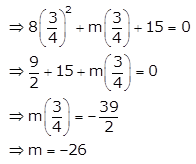
So, the equation (i) becomes 8x² – 26x + 15 = 0
⇒ 8x² – 20x – 6x + 15 = 0
⇒ 4x(2x – 5) -3(2x – 5) = 0
⇒ (4x – 3)(2x – 5) = 0
⇒ x = \(\frac{3}{4}\) or x = \(\frac{5}{2}\)
⇒ x = \(\frac{3}{4}, \frac{5}{2}\)
Hence, the other root is \(\frac{5}{2}\)

Question 3.
One root of the quadratic equation x² – 3x – 2ax – 6a = 0 is -3, find its other root.
Solution:
Given quadratic equation is …. (i)
One of the roots of (i) is -3, so it satisfies (i)
⇒ x² – 3x – 2ax – 6a = 0
⇒ x(x + 3) – 2a(x + 3) = 0
⇒ (x – 2a)(x + 3) = 0
⇒ x = -3, 2a
Hence, the other root is 2a.

Question 4.
If p – 15 = 0 and 2x² + 15x + 15 = 0;find the values of x.
Solution:
Given i.e p – 15 = 0 i.e. p = 15
So, the given quadratic equation becomes
2x² + 15x + 15 = 0
⇒ 2x + 10x + 5x + 15 = 0
⇒ 2x(x + 5) + 5(x + 5)
⇒ (2x + 5)(x + 5) = 0
⇒ x = -5, \(-\frac{5}{2}\)
Hence, the values of x are -5 and \(-\frac{5}{2}\)

Question 5.
Find the solution of the equation 2x² -mx – 25n = 0; if m + 5 = 0 and n – 1 = 0.
Solution:
Given quadratic equation is 2x² -mx – 25n = 0 ….. (i)
Also, given and m + 5 = 0 and n – 1 = 0
⇒ m = -5 and n = 1
So, the equation (i) becomes
2x² + 5x + 25 = 0
⇒ 2x + 10x – 5x – 25 = 0
⇒ 2x(x + 5) -5(x + 5) = 0
⇒ (x + 5)(2x – 5) = 0
⇒ x = -5, \(\frac{5}{2}\)
Hence, the solution of given quadratic equation are x and \(\frac{5}{2}\)

Question 6.
If m and n are roots of the equation \(\frac{1}{x}-\frac{1}{x-2}=3\) where x ≠ 0 and x ≠ 2; find m × n.
Solution:
Given quadratic equation is \(\frac{1}{x}-\frac{1}{x-2}=3\)

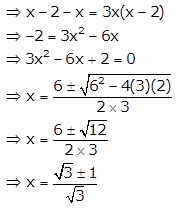
Since, m and n are roots of the equation, we have

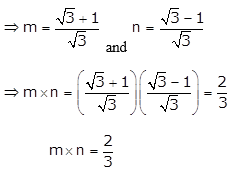
Question 7.
Solve, using formula :
x² + x – (a + 2)(a + 1) = 0
Solution:
Given quadratic equation is x² + x – (a + 2)(a + 1) = 0
Using quadratic formula,

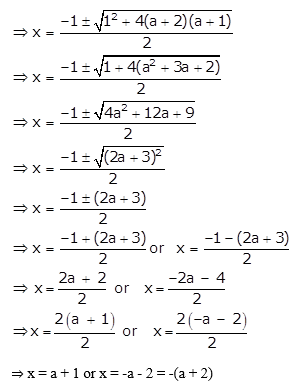
Question 8.
Solve the quadratic equation 8x² – 14x + 3 = 0
(i) When x ∈ I (integers)
(ii) When x ∈ Q (rational numbers)
Solution:
Given quadratic equation is 8x² – 14x + 3 = 0
⇒ 8x² – 12x – 2x + 3 = 0
⇒ 4x(2x – 3) – (2x – 3) = 0
⇒ (4x – 1)(2x – 3) = 0
⇒ x = \(\frac{3}{2}\) or x = \(\frac{1}{4}\)
(i) When x ϵ I, the equation 8x² – 14x + 3 = 0 has no roots
(ii) When x ϵ Q the roots of 8x² – 14x + 3 = 0 are
x = \(\frac{3}{2}\) x = \(\frac{1}{4}\)

Question 9.
Find the value of m for which the equation (m + 4 )² + (m + 1)x + 1 = 0 has real and equal roots.
Solution:
Given quadratic equation is (m + 4 )² + (m + 1)x + 1 = 0
The quadratic equation has real and equal roots if its discriminant is zero.
⇒ D = b² – 4ac = 0
⇒ (m + 1)² -4(m + 4)(1) = 0
⇒ m² + 2m + 1 – 4m – 16 = 0
⇒ m² – 2m – 15 = 0
⇒ m² – 5m + 3m – 15 = 0
⇒ m(m – 5) +3(m =5) = 0
⇒ (m – 5)(m + 3) = 0
⇒ m = 5 or m = -3

Question 10.
Find the values of m for which equation 3x² + mx + 2 = 0 has equal roots. Also, find the roots of the given equation.
Solution:
Given quadratic equation is 3x² + mx + 2 = 0 …. (i)
The quadratic equation has equal roots if its discriminant is zero
⇒ D = b² – 4ac = 0
⇒ m² – 4(2)(3) = 0
⇒ m² = 24
⇒ m = \(\pm 2 \sqrt{6}\)
When m = \(2 \sqrt{6}\), equation (i) becomes

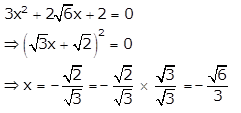
When m = \(-2 \sqrt{6}\), equation (i) becomes

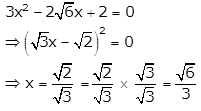
∴ x= \(-\frac{\sqrt{6}}{3}, \frac{\sqrt{6}}{3}\)

Question 11.
Find the value of k for which equation 4x² + 8x – k = 0 has real roots.
Solution:
Given quadratic equation is 4x² + 8x – k = 0 …. (i)
The quadratic equation has real roots if its discriminant is greater than or equal to zero
⇒ D = b² – 4ac ≥ 0
⇒ 8² – 4(4)(-k) ≥ 0
⇒ 64 + 16k ≥ 0
⇒ 16k ≥ -64
⇒ k ≥ -4
Hence, the given quadratic equation has real roots for k ≥ -4

Question 12.
Find, using quadratic formula, the roots of the following quadratic equations, if they exist
(i) 3x² – 5x + 2 = 0
(ii) x² + 4x + 5 = 0
Solution:
(i) Given quadratic equation is 3x² – 5x + 2 = 0
D = b² – 4ac = (-5)² – 4(3)(2) = 25 – 24 = 1
Since D > 0, the roots of the given quadratic equation are real and distinct.
Using quadratic formula, we have

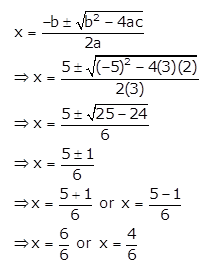
⇒ x = 1 or x = \(\frac{2}{3}\)

(ii) Given quadratic equation is x² + 4x + 5 = 0
D = b² – 4ac = (4)² – 4(1)(5) = 16 – 20 = – 4
Since D < 0, the roots of the given quadratic equation does not exist.

Solution 13:
(i) Given quadratic equation is \(\frac{1}{18-x}-\frac{1}{18+x}=\frac{1}{24}\)

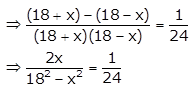
⇒ 48x = 324 – x²
⇒ x² + 48x – 324 = 0
⇒ x² + 54x – 6x – 324 = 0
⇒ x(x + 54) -6(x + 54) = 0
⇒ (x + 54)(x – 6) = 0
⇒ x = -54 or x = 6
But as x > 0, so x can’t be negative.
Hence, x = 6.
(ii) Given quadratic equation is \((x-10)\left(\frac{1200}{x}+2\right)=1260\)
⇒ (x – 10)\(\left(\frac{1200+2 x}{x}\right)\) = 1260
⇒ (x – 10)(1200 + 2x) = 1260x
⇒ 1200x + 2x² – 12000 – 20x = 1260x
⇒ 2x² – 12000 – 80x = 0
⇒ x² – 40x – 6000 = 0
⇒ x² – 100x + 60x – 6000 = 0
⇒ (x – 100)(x – 60) = 0
⇒ x = 100 or x = -60
But as x < 0, so x can’t be positive.
Hence, x = -60.

More Resources for Selina Concise Class 10 ICSE Solutions

• Concise Mathematics Class 10 ICSE Solutions
• Concise Physics Class 10 ICSE Solutions
• Concise Chemistry Class 10 ICSE Solutions
• Concise Biology Class 10 ICSE Solutions

ICSE Solutions Selina ICSE Solutions