Selina Concise Mathematics Class 6 ICSE Solutions Chapter 29 The Circle
Selina Publishers Concise Mathematics Class 6 ICSE Solutions Chapter 29 The Circle
ICSE SolutionsSelina ICSE SolutionsML Aggarwal Solutions
APlusTopper.com provides step by step solutions for Selina Concise ICSE Solutions for Class 6 Mathematics. You can download the Selina Concise Mathematics ICSE Solutions for Class 6 with Free PDF download option. Selina Publishers Concise Mathematics for Class 6 ICSE Solutions all questions are solved and explained by expert mathematic teachers as per ICSE board guidelines.
Selina Class 6 Maths ICSE SolutionsPhysicsChemistryBiologyGeographyHistory & Civics
IMPORTANT POINTS
1. A circle is a round enclosed figure, whose mid-point is called its centre.
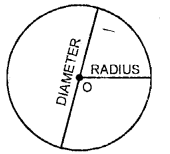
2. The line segment joining the centre to any point on the circle is called a radius. A centre has infinite radii and all radii of a circle are equal.
3. A line segment which contains the centre of the circle and whose ends points lie on the circle is called diameter of the circle. Diameters of a circle are also equal.
4. Parts of a circle: A circle has three parts (i) Interior (ii) Exterior and (iii) Circle itself.
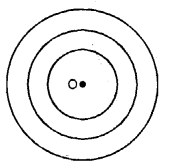
5. Concentric circles: Two or more circles having the same centre but different radii are called concentric circles.
6. Chord of a circle: A line which divides the circle into two parts is called chord of the circle. Diameter is the longest chord of the circle.
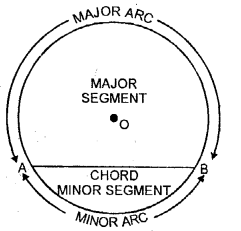
7. Segment of a circle: When a chord divides the circle into two unequal parts, the bigger part is called the major segment and smaller part is called the minor segment.
8. Arc of a circle: A part of circumference of a circle is called an arc of the circle. Arc greater than half circle is called the major arc and less than half circle is called the minor arc.
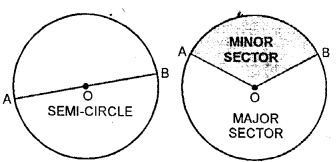
9. Sector of a circle: A diameter divides the circle into two equal parts and each part is called a semicircle. Sector greater than a semi-circle is called the major sector and less than semi-circle is called the minor sector of the circle.
The Circle Exercise 29A – Selina Concise Mathematics Class 6 ICSE Solutions
Question 1.
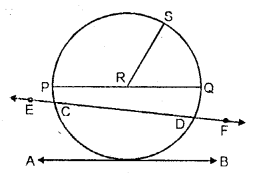
Use the figure given below to fill in the blanks :
(i) R is the …… of the circle.
(ii) Diameter of a circle is …… .
(iii) Tangent to a circle is … .
(iv) EF is a …… of the circle.
(v) …… is a chord of the circle.
(vi) Diameter = 2 x …..
(vii) ……. is a radius of the circle.
(viii) If the length of RS is 5 cm, the length of PQ = ……
(ix) If PQ is 8 cm long, the length of RS =…..
(x) AB is a ….. of the circle
Solution:
(i) center
(ii) PQ
(iii)AB
(iv) secant
(v) CD
(vi) radius
(vii) RS
(viii) 10 cm
(ix) 4 cm
(x) tangent.
Question 2.
Draw a circle of radius 4.2 cm. Mark its centre as O. Take a point A on the circumference of the circle. Join AO and extend it till it meets point B on the circumference of the circle,
(i) Measure the length of AB.
(ii) Assign a special name to AB.
Solution:
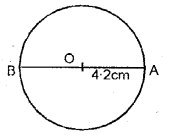
(i) By measurement AB = 8.4 cm.
(ii) ∴ AB is the diameter of the circle.
Question 3.
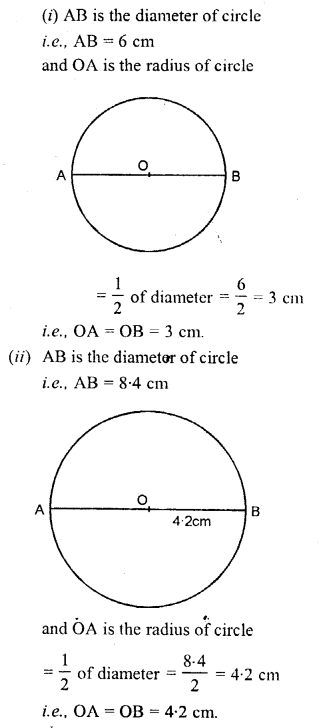
Draw circle with diameter :
(i) 6 cm
(ii) 8.4 cm.
In each case, measure the length of the radius of the circle drawn.
Solution:
Question 4.
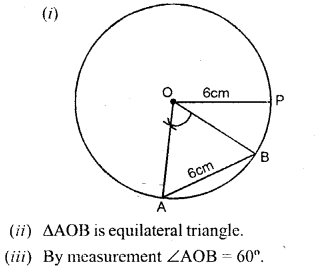
Draw a circle of radius 6 cm. In the circle, draw a chord AB = 6 cm.
(i) If O is the centre of the circle, join OA and OB.
(ii) Assign a special name to ∆AOB
(iii) Write the measure of angle AOB.
Solution:
Question 5.
Draw a circle of radius 4.8 cm and mark its centre as P.
(i) Draw radii PA and PB such that ∠APB = 45°.
(ii) Shade the major sector of the circle
Solution:
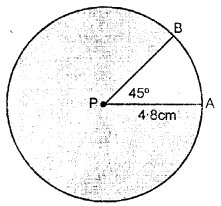
PA is the radius of circle. i.c., PA = 4.8 cm.
(i) ∠APB = 45° in which P is the centre of the circle and PA and PB are radii of circle.
(ii) Major sector of circle is shaded in the figure.
Question 6.
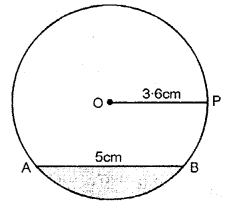
Draw a circle of radius 3.6 cm. In the circle, draw a chord AB = 5 cm. Now shade the minor segment of the circle.
Solution:
Shaded portion of circle is the minor segment of the circle.
Question 7.
Mark two points A and B ,4cm a part, Draw a circle passing through B and with A as a center
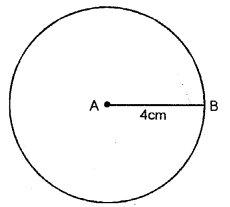
Solution:
In the figure, A is the centre of the circle and AB = 4 cm [radius of circle]
Question 8.
Draw a line AB = 8.4 cm. Now draw a circle with AB as diameter. Mark a point C on the circumference of the circle. Measure angle ACB.
Solution:
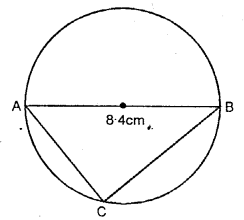
By measurement ∠ACB =90
The Circle Exercise 29B – Selina Concise Mathematics Class 6 ICSE Solutions
Question 1.
Construct a triangle ABC with AB = 4.2 cm, BC = 6 cm and AC = 5cm. Construct the circumcircle of the triangle drawn.
Solution:
Steps of Construction :
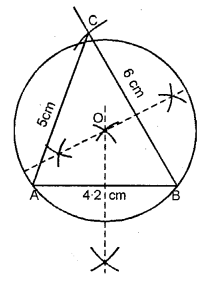
(i) Draw ∆ABC in which AB = 4.2 cm. BC = 6 cm. and AC = 5 cm.
(ii) Draw the perpendicular bisectors of any two sides of the triangle. Let these intersect at O.
(iii) Taking O as centre and OA or OB or OC as radius draw a circle.
This circle will pass through vertices A, B and C.
Question 2.
Construct a triangle PQR with QR = 5.5 cm, ∠Q = 60° and angle R = 45°.
Construct the circumcircle cif the triangle PQR.
Solution:
Steps of Construction :
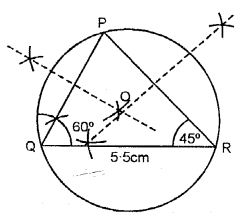
(i) Draw a ∆PQR in which QR = 5.5 cm, ∠Q = 60° and ∠R = 45°.
(ii) Draw the arc bisector of PQ and PR which intersect at O.
(iii) Taking O as centre and radius OP or OQ or OR draw a circle.
This circle will pass through vertices P, Q and R.
Question 3.
Construct a triangle ABC with AB = 5 cm, ∠B = 60° and BC = 6. 4 cm.
Draw the incircle of the triangle ABC. Sol. Steps of Construction :
Solution:
Steps of Construction:
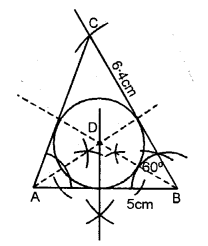
(i) Draw a line AB = 5 cm.
(ii)B as a centre draw an angle with the help of compass ∠B = 60°. Cut the line with an arc BC = 6 4 cm.
(iii) Join AC.
(iv) Now, from A and B cut the bisector of ∠A and ∠B, which intersect each other at point D.
(v) With D as a centre draw an incircle which touches all the three sides of AABC.
Question 4.
Construct a triangle XYZ in which XY = YZ= 4.5 cm and ZX = 5.4 cm. Draw the circumcircle of the triangle and measure its circumradius.
Solution:
Steps of Construction :
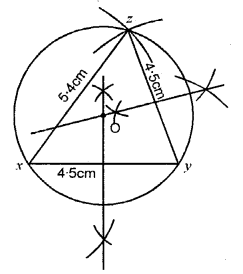
(i) Draw a triangle XYZ in which XY = YZ = 4.5 cm and ZX = 5.4 cm.
(ii) Draw the bisectors of XZ and YZ which meet at O.
(iii) With O as centre and radius OX or OY or OZ draw a circle.
This circle will pass through X, Y and Z.
Question 5.
Construct a triangle PQR in which, PQ = QR = RP = 5.7 cm. Draw the incircle of the triangle and measure its radius.
Solution:
Steps of Construction :
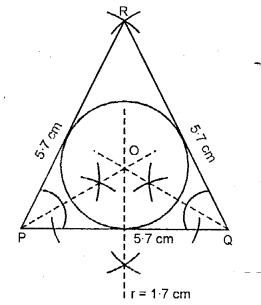
(i) Draw an equilateral ∆ RPQ in which PQ = QR = RP = 5.7 cm each.
(ii) From P and Q cut the bisector of ∠P and ∠Q, which intersect each other at point O.
(iii) With P as a centre draw an incircle which touches all the three sides of ∆RPQ.
The Circle Revision Exercise – Selina Concise Mathematics Class 6 ICSE Solutions
Question 1.
The centre of a circle is at point O and its radius is 8 cm. State the position of a point P (point P may lie inside the circle, on the circumference of the circle, or outside the circle), when :
(a) OP = 10.6 cm
(b) OP = 6.8 cm
(c) OP = 8 cm
Solution:
(a) Draw circle each of radius 8 cm. With centre O
In figure (i) draw OP = 10.6 cm
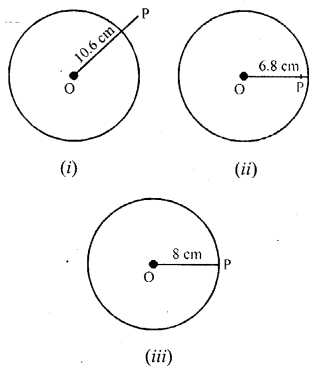
We see that point P lies outside the circle as OP > radius of the circle
(b) In figure (ii) OP = 6.8 cm. We see that P lies inside the circle as OP < radius of the circle.
(c) In figure, OP = 8 cm. We see that P lies on the circle as OP = radius of the circle.
Question 2.
The diameter of a circle is 12.6 cm. State, the length of its radius.
Solution:
Diameter of the circle = 12.6 cm
∴Radius = \(\frac { 1 }{ 2 }\) diameter = \(\frac { 1 }{ 2 }\) x 12.6 cm
= 6.3 cm
Question 3.
Can the length of a chord of a circle be greater than its diameter ? Explain.
Solution:
No, the length of chord cannot be greater than the diameter of the cirlce as the diameter of a circle is the greatest chord of that circle.
Question 4.
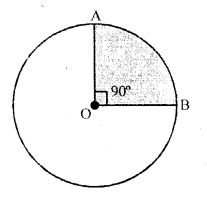
Draw a circle of diameter 7 cm. Draw two radii of this circle such that the angle between these radii is 90°. Shade the minor sector obtained. Write a special name for this sector.
Solution:
Draw a circle with diameter = 7 cm
OA and OB are the radii of the circle such that ∠AOB = 90°
Now shade the minor sector AOB This is the quadrant of the circle
Question 5.
State, which of following statements are true and which are false :
(i) If the end points A and B of the line segment lie on the circumference of a circle, AB is a diameter.
(ii) The longest chord of a circle is its diameter.
(iii) Every diameter bisects a circle and each part of the circle so obtained is a semi-circle.
(iv) The diameters of a circle always pass through the same point in the circle.
Solution:
(i) False, as AB may be diameter or may not be, it can be chord.
(ii) True, diameter of a circle is the longest chord.
(iii) True.
(iv) True, all the diameter of a circle pass through the same point i.e., centre, of the circle.