Selina Concise Mathematics Class 6 ICSE Solutions Chapter 27 Quadrilateral
Selina Publishers Concise Mathematics Class 6 ICSE Solutions Chapter 27 Quadrilateral
ICSE SolutionsSelina ICSE SolutionsML Aggarwal Solutions
APlusTopper.com provides step by step solutions for Selina Concise ICSE Solutions for Class 6 Mathematics. You can download the Selina Concise Mathematics ICSE Solutions for Class 6 with Free PDF download option. Selina Publishers Concise Mathematics for Class 6 ICSE Solutions all questions are solved and explained by expert mathematic teachers as per ICSE board guidelines.
Selina Class 6 Maths ICSE SolutionsPhysicsChemistryBiologyGeographyHistory & Civics
IMPORTANT POINTS
4.Quadrilateral: A quadrilateral is a plane figure enclosed by four sides. It has four sides, four interior angles and four vertices.
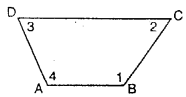
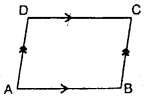
In quadrilateral ABCD, shown alongside:
(i) four sides are : AB, BC, CD and DA.
(ii) four angles are : ∠ABC,∠BCD, ∠CDA and ∠DAB ; which are numbered∠1, ∠2, ∠3 and ∠4 respectively.
(iii) four vertices are : A, B, C and D.
5. Diagonals of a Quadrilateral : The line segments joining the opposite vertices of a quadrilateral are called its diagonals.
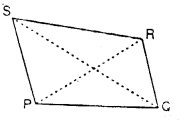
The given figure shows a quadrilateral PQRS with diagonals PR and QS.
6. Types of Quadrilaterals :
1. Trapezium: A trapezium is a quadrilateral in which one pair of opposite sides are parallel.
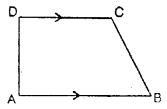
The figure, given alongside, shows a trapezium as its sides AB and DC are parallel i.e. AB || DC.
When the non-parallel sides of the trapezium are equal in length, it is called an isosceles trapezium.
The given figure shows a trapezium ABCD whose non-parallel sides AD and BC are equal in length i.e. AD = BC; therefore it is an isosceles trapezium.
Also, in an isosceles trapezium :
(i) base angles are equal:
i.e. ∠A = ∠B and ∠D =∠C
(ii) diagonals are equal
i.e. AC = BD.
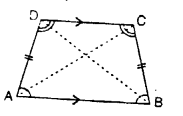
2.Parallelogram : A parallelogram is a quadrilateral, in which both the pairs of opposite sides are parallel.
The quadrilateral ABCD, drawn alongside, is a parallelogram; since, AB is parallel to DC and AD is parallel to BC i.e.
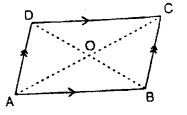
AB || DC and AD || BC.
Also, in a parallelogram ABCD:
(i) opposite sides are equal:
i.e. AB = DC and AD = BC.
(ii) opposite angles are equal:
i.e. ∠ABC = ∠ADC and ∠BCD = ∠BAD
(iii) diagonals bisect each other :
i.e. OA = OC = \(\frac { 1 }{ 2 }\) AC and OB = OD = \(\frac { 1 }{ 2 }\) BD.
7. Some special types of Parallelograms
(a) Rhombus : A rhombus is a parallelogram in which all its sides are equal.
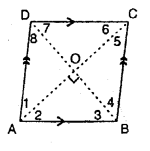
∴In a rhombus ABCD :
(i) opposite sides are parallel:
i.e. AB||DC and AD||BC.
(ii) all the sides are equal:
i.e. AB = BC = CD = DA.
(iii) opposite angles are equal:
i.e. ∠A = ∠C and ∠B = ∠D.
(iv) diagonals bisect each other at right angle :
i.e. OA= OC = \(\frac { 1 }{ 2 }\) AC ; OB = OD = \(\frac { 1 }{ 2 }\) BD.
and ∠AOB= ∠BOC = ∠COD = ∠AOD = 90°
(v) diagonals bisect the angles at the vertices :
i.e. ∠1 =∠2 ;∠3 = ∠4 ; ∠5 = ∠6 and ∠7 =∠8.
(b) Rectangle : A rectangle is a parallelogram whose any angle is 90°.
A rectangle is also defined as a quadrilateral whose each angle is 90°.
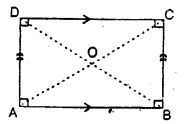
Note : If any angle of a parallelogram is 90° ; automatically its each angle is 90° ; the reason being that the opposite angles of a parallelogram are equal.
Also, in a rectangle:
(i) opposite sides are parallel.
(ii) opposite sides are equal.
(iii) each angle is 90°.
(iv) diagonals are equal.
(v) diagonals bisect each other.
(c) Square : A square is a parallelogram, whose all side are equal and each angle is 90°.
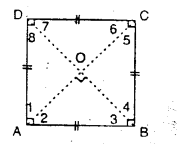
A square can also be defined as :
(i) a rhombus whose any angle is 90°.
(ii) a rectangle whose all sides are equal.
(iii) a quadrilateral whose all sides are equal and each angle is 90°.
∴ If ABCD is a square :
(i) all its sides are equal, i.e. AB = BC = CD = DA
(ii) each angle of it is 90°.
i.e. ∠A = ∠B = ∠C = ∠D = 90°.
Also,
(iii) diagonals are equal.
i.e. AC = BD.
(iv) diagonals bisect each other at 90°.
i.e. OA = OC =\(\frac { 1 }{ 2 }\) AC;OB = OD = \(\frac { 1 }{ 2 }\) BD
and ∠AOB = ∠BOC = ∠COD = ∠DOA = 90°.
Since, diagonals AC and BD are equal; therefore ; OA = OC = OB = OD.
(v) diagonals bisect the angles at the vertices
i.e. ∠1 = ∠2 = 45° [∵ ∠1 + ∠2 = 90°]
Similarly; ∠3 = ∠4 = 45° ;
∠5 – ∠6 = 45° and ∠7 = ∠8 = 45°.
Quadrilateral Exercise 27A – Selina Concise Mathematics Class 6 ICSE Solutions
Question 1.
Two angles of a quadrilateral are 89° and 113°. If the other two angles are equal; find the equal angles.
Solution:
Let the other angle = x°
According to given,
89° + 113° + x° + x° = 360°
2x° = 360° – 202°
2x° = 158°
x° = \(\frac { 158 }{ 2 }\) =79°
∴other two angles = 79° each
Question 2.
Two angles of a quadrilateral are 68° and 76°. If the other two angles are in the ratio 5 : 7; find the measure of each of them.
Solution:
Two angles are 68° and 76°
Let other two angles be 5x and 7x
∴ 68°+76°+5x + 7x = 360°
12x + 144° = 360°
12x = 360° – 144°
12x= 216°
x = 18°
angles are 5x and 7x
i.e. 5×18° and 7×18° i.e. 90° and 126°
Question 3.
Angles of a quadrilateral are (4x)°, 5(x+2)°, (7x-20)° and 6(x+3)°. Find
(i) the value of x.
(ii) each angle of the quadrilateral.
Solution:
Angles of quadrilateral are,
(4x)°, 5(x+2)°, (7x-20)° and 6(x+3)°.
4x+5(x+2)+(7x-20)+6(x+3) = 360°
4x+5x+10+7x-20+6x+18 = 360° 22x+8 = 360°
22x = 360°-8°
22x = 352°
x = 16°
Hence angles are,
(4x)° = (4×16)° = 64°,
5(x+2)° = 5(16+2)° = 90°,
(7x-20)° = (7×16-20)° = 92°
6(x+3)° = 6(16+3) = 114°
Question 4.
Use the information given in the following figure to find :
(i) x
(ii) ∠B and ∠C
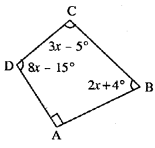
Solution:
∵ ∠A = 90° (Given)
∠B = (2x+4°)
∠C = (3x-5°)
∠D = (8x – 15°)
∠A + ∠B + ∠C + ∠D = 360°
90° + (2x + 4°) + (3x – 5°) + (8x – 15°) = 360°
90° + 2x + 4° + 3x – 5° + 8x – 15° = 360°
⇒ 74° + 13x = 360°
⇒13x = 360° – 74°
⇒ 13x = 286°
⇒ x = 22°
∵ ∠B = 2x + 4 = 2. x 22° + 4 – 48°
∠C = 3x – 5 = 3×22° -5 = 61°
Hence (i) 22° (ii) ∠B = 48°, ∠C = 61°
Question 5.
In quadrilateral ABCD, side AB is parallel to side DC. If ∠A : ∠D = 1 : 2 and ∠C : ∠B = 4:5
(i) Calculate each angle of the quadrilateral.
(ii) Assign a special name to quadrilateral ABCD.
Solution:
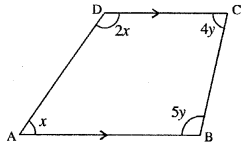
∵∠A : ∠D = 1:2
Let ∠A = x and ∠B = 2x
∵∠C : ∠B = 4 : 5 Let ∠C = 4y and ∠B = 5y
∵AB || DC
∠A + ∠D = 180° x + 2x = 180°
3x = 180° x = 60°
∴A = 60°
∠D = 2x = 2 x 60 = 120° Again ∠B + ∠C = 180°
5y + 4y= 180°
9y = 180°
y = 20°
∴∠B = 5y- = 5 x 20 = 100°
∠C = 4y = 4 x 20 = 80°
Hence ∠A = 60° ; ∠B = 100° ; ∠C = 80° and ∠D = 120°
Question 6.
From the following figure find ;
(i) x,
(ii) ∠ABC,
(iii) ∠ACD.
Solution:
(i) In Quadrilateral ABCD,
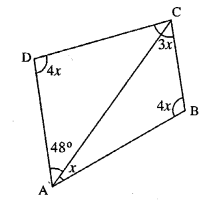
x + 4x + 3x + 4x + 48° = 360°
12x = 360° – 48°
12x =312
(ii) ∠ABC = 4x
4 x 26 = 104°
(iii) ∠ACD = 180°-4x-48°
= 180°-4×26°-48°
= 180°-104°-48°
= 180°-152° = 28°
Question 7.
Given : In quadrilateral ABCD ; ∠C = 64°, ∠D = ∠C – 8° ;
∠A = 5(a+2)° and ∠B = 2(2a+7)°.
Calculate ∠A.
Solution:
∵∠C = 64° (Given)
∴∠D = ∠C- 8°
= 64°- 8°
= 56°
∠A = 5 (a + 2)°
∠B = 2(2a + 7)°
Now ∠A + ∠B + ∠C + ∠D = 360°
5(a + 2)° + 2(2a + 7)° + 64°+ 56° = 360°
5a + 10 + 4a + 14° + 64° + 56° = 360°
9a + 144° = 360°
9a = 360°-144°
9a = 216°
a = 24°
∴∠A = 5(a + 2)
= 5(24 + 2)
= 130°
Question 8.
In the given figure :
∠b = 2a + 15
and ∠c = 3a+5; find the values of b and c.
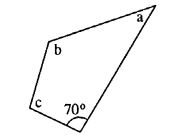
Solution:
∠b = 2a + 15
& ∠c = 3a + 5
∵Sum of angles of quadrilateral = 360°
70° + a + 2a + 15 + 3a + 5 – 360°
6a+90° = 360°
6a = 270°
a = 45°
∴ b = 2a+15= 2×45+15 = 105°
c = 3a+5 = 3×45+5 = 140°
105° and 140°
Question 9.
Three angles of a quadrilateral are equal. If the fourth angle is 69°; find the measure of equal angles.
Solution:
Let each equal angle be
x° x + x + x + 69° = 360°
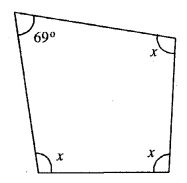
3x = 360°-69 3x =291 x = 97°
Each equal angle = 97°
Question 10.
In quadrilateral PQRS, ∠P : ∠Q : ∠R : ∠S = 3 : 4 : 6 : 7.
Calculate each angle of the quadrilateral and then prove that PQ and SR are parallel to each other. Is PS also parallel to QR ?
Solution:
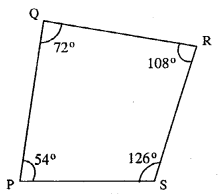
∵∠P : ∠Q : ∠R : ∠S = 3 : 4 : 6 : 7
Let ∠P = 3x
∠Q = 4x
∠R = 6x & ∠S = 7x
∴∠P+∠Q+∠R+∠S = 360°
3x + 4x + 6x + lx = 360°
20x = 360°
x = 18°
∴ ∠P = 3x = 3×18 = 54°
∠Q = 4x = 4×18 = 72°
∠R = 6x = 6×18 = 108°
∠S = 7x = 7×18 = 126°
∠Q + ∠R = 72°+108° = 180° or ∠P +∠S = 54°+126° = 180°
Hence PQ || RS
As ∠P + ∠Q = 72° +54° = 126°
Which is * 180°.
∴PS and QR are not parallel.
Question 11.
Use the information given in the following figure to find the value of x.
Solution:
Take A, B, C, D as the vertices of quadrilateral and BA is produced to E (say).
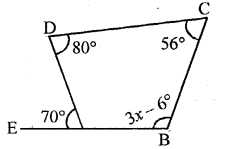
Since ∠EAD = 70°
∴∠DAB = 180° – 70° = 110° [∵ EAB is a straight line and AD stands on it]
∴∠EAD + ∠DAB = 180°
∴110° + 80° + 56° + 3x = 360°
[∵ sum of interior angles of a quadrilateral = 360°]
∴3x = 360° – 110° – 80° – 56° + 6°
3x = 360° – 240° = 120°
∴x = 40°
Question 12.
The following figure shows a quadrilateral in which sides AB and DC are parallel.
If ∠A : ∠D = 4 : 5, ∠B = (3x – 15)° and ∠C = (4x + 20)°, find each angle of the quadrilateral ABCD.
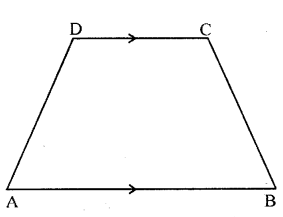
Solution:
Let ∠A = 4x
∠D = 5x
Since ∠A + ∠D = 180° [∵ AB || DC]
∴4x + 5x = 180°
⇒ 9x = 180° ⇒x = 20°
∴∠A = 4 (20) = 80°, ∠D = 5 (20) = 100° Again ∠B + ∠C = 180° [ ∵ AB || DC]
∴ 3x – 15° + 4x + 20° = 180°
7x = 180°-5°
⇒ 7x = 175° ⇒ x = 25°
∴∠B = 75°-15° = 60° and ∠C = 4(25) + 20 = 100° + 20° = 120°
Quadrilateral Exercise 27B – Selina Concise Mathematics Class 6 ICSE Solutions
Question 1.
In a trapezium ABCD, side AB is parallel to side DC. If ∠A = 78° and ∠C = 120°, find angles B and D.
Solution:
∵ AB || DC and BC is transversal
∴∠B and ∠C, ∠A and ∠D are Cointerior angles with their sum = 180°
i.e. ∠B + ∠C = 180°
⇒ ∠B + 120° = 180°
⇒ ∠B = 180° – 120°
⇒ ∠B = 60°
Also ∠A + ∠D = 180°
⇒ 78° + ∠D = 180°
⇒ ∠D = 180° – 78°
∠D = 102°
Question 2.
In a trapezium ABCD, side AB is parallel to side DC. If ∠A = x° and ∠D = (3x – 20)°; find the value of x.
Solution:
∵AB || DC and BC is transversal
∴∠A and ∠B are Co-interior angles with their sum = 180°
i.e. ∠A + ∠D = 180°
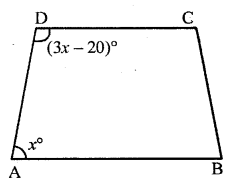
⇒ x° + (3x – 20)° = 180°
⇒ x° + 3x° – 20° = 180°
⇒ 4x° = 180° + 20°
x° = \(\frac { 200 }{ 4 }\) = 50°
∴Value of x = 50°
Question 3.
The angles A, B, C and D of a trapezium ABCD are in the ratio 3 : 4 : 5 : 6.
Le. ∠A : ∠B : ∠C : ∠D = 3:4: 5 : 6. Find all the angles of the trapezium. Also, name the two sides of this trapezium which are parallel to each other. Give reason for your answer
Solution:


Question 4.
In an isosceles trapezium one pair of opposite sides are ….. to each Other and the other pair of opposite sides are ….. to each other.
Solution:
In an isosceles trapezium one pair of opposite sides are parallel to each other and the other pair of opposite sides are equal to each other.
Question 5.
Two diagonals of an isosceles trapezium are x cm and (3x – 8) cm. Find the value of x.
Solution:
∵The diagonals of an isosceles trapezium are of equal length
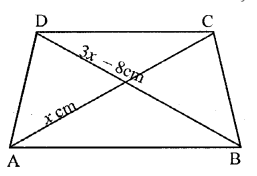
∴3x – 8 = x
⇒ 3x – x = 8 cm
⇒ 2x = 8 cm
⇒ x = 4 cm
∴ The value of x is 4 cm
Question 6.
Angle A of an isosceles trapezium is 115° ; find the angles B, C and D.
Solution:
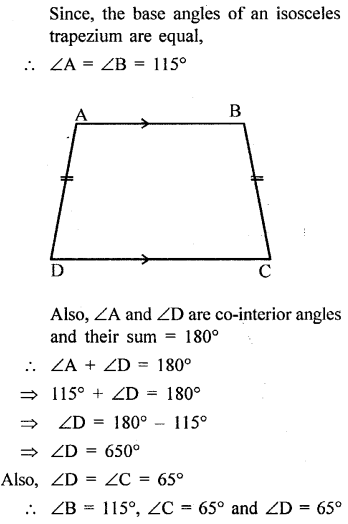
Question 7.
Two opposite angles of a parallelogram are 100° each. Find each of the other two opposite angles.
Solution:
Given : Two opposite angles of a parallelogram are 100° each
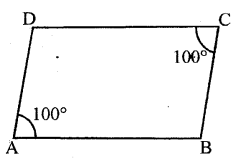
∵ Adjacent angles of a parallelogram are supplementary,
∴∠A + ∠B = 180°
⇒ 100° + ∠B = 180°
⇒ ∠B = 180° – 100°
⇒ ∠B = 80°
Also, opposite angles of a parallelogram are equal
∴∠D = ∠B = 80°
∴∠B = ∠D = 80°
Question 8.
Two adjacent angles of a parallelogram are 70° and 110° respectively. Find the other two angles of it.
Solution:
Given two adjacent angles of a parallelogram are 70° and 110° respectively.
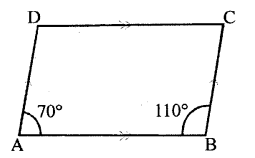
Since, we know that opposite angles of a parallelogram are equal
∴∠C = ∠A = 70° and ∠D = ∠B = 110°
Question 9.
The angles A, B, C and D of a quadrilateral are in the ratio 2:3: 2 : 3. Show this quadrilateral is a parallelogram.
Solution:


Question 10.
In a parallelogram ABCD, its diagonals AC and BD intersect each other at point O.
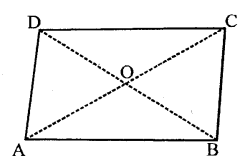
If AC = 12 cm and BD = 9 cm ; find; lengths of OA and OD.
Solution:
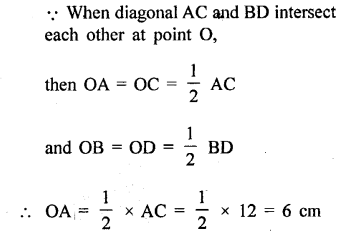
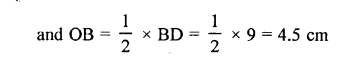
Question 11.
In parallelogram ABCD, its diagonals intersect at point O. If OA = 6 cm and OB = 7.5 cm, find the length of AC and BD.
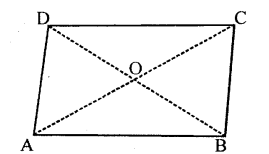
Solution:

Question 12.
In parallelogram ABCD, ∠A = 90°
(i) What is the measure of angle B.
(ii) Write the special name of the paralleogram.
Solution:
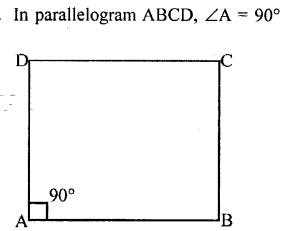

Question 13.
One diagnol of a rectangle is 18 cm. What is the length of its other diagnol?
Solution:
∵ In a rectangle, diagnols are equal
⇒ AC = BD
Given, one diagnol of a rectangle = 18cm
∴ Other diagnol of a rectangle will be = 18cm
i.e. AC = BD = 18cm.
Question 14.
Each angle of a quadrilateral is x + 5°. Find :
(i) the value of x
(ii) each angle of the quadrilateral.
Give the special name of the quadrilateral taken.
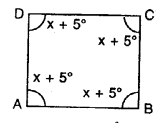
Solution:


Question 15.
If three angles of a quadrilateral are 90° each, show that the given quadrilateral is a rectangle.
Solution:
The given quadrilateral ABCD will be a rectangle, if its each angle is 90°
Since, the sum of interior angles of a quadrilateral is 360°.
∴∠A +∠B + ∠C + ∠D = 360°
⇒ 90° + 90° + 90° + ∠D = 360°
⇒ 270° + ∠D = 360°
⇒ ∠D = 360° – 270°
⇒ ∠D = 90°
Since, each angle of the quadrilateral is 90°.
∴The given quadrilateral is a rectangle.
Question 16.
The diagnols of a rhombus are 6 .cm and 8 cm. State the angle at which these diagnols intersect.
Solution:
The diagnols of a Rhombus always intersect at 90°.
Question 17.
Write, giving reason, the name of the figure drawn alongside. Under what condition will this figure be a square.
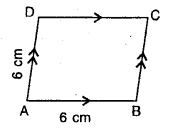
Solution:
Since, all the sides of the given figure are equal.
i.e. AB = BC = CD = DA = 6 cm
∴ The given figure is a rhombus.
This figure shall be considered as a square, if any angle is 90°.
Question 18.
Write two conditions that will make the adjoining figure a square.
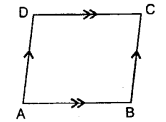
Solution:
The conditions that will make the ad-joining figure a square are :
(i) All the sides must be equal.
(ii) Any angle is 90°.