Selina Concise Mathematics Class 6 ICSE Solutions Chapter 7 Number Line
Selina Publishers Concise Mathematics Class 6 ICSE Solutions Chapter 7 Number Line
ICSE SolutionsSelina ICSE SolutionsML Aggarwal Solutions
APlusTopper.com provides step by step solutions for Selina Concise ICSE Solutions for Class 6 Mathematics. You can download the Selina Concise Mathematics ICSE Solutions for Class 6 with Free PDF download option. Selina Publishers Concise Mathematics for Class 6 ICSE Solutions all questions are solved and explained by expert mathematic teachers as per ICSE board guidelines.
Selina Class 6 Maths ICSE SolutionsPhysicsChemistryBiologyGeographyHistory & Civics
IMPORTANT POINTS
- Number Line : A Number line is used to represent numbers, such as : fractions, whole numbers, integers, etc.
- Using A Number Line to Compare Numbers : Out of any two numbers, marked on a number line, the number which is on the right of the other number is greater and the number which is on the left of the other number is lesser (smaller).
Number Line Exercise 7A – Selina Concise Mathematics Class 6 ICSE Solutions
Question 1.
Fill in the blanks, using the following number line :
![]()
(i) An integer, on the given number line, is ………… than every number on its left.
(ii) An integer, on the given number line, is greater than every number to its …………..
(iii) 2 is greater than – 4 implies 2 is to the ………….. of – 4.
(iv) -3 is ………….. than 2 and 3 is ………. than – 2.
(v) – 4 is ………….. than -8 and 4 is …………… than 8.
(vi) 5 is …………. than 2 and -5 is …………… than – 2.
(vii) -6 is …………. than 3 and the opposite of -6 is ………… than opposite of 3.
(viii) 8 is …………. than -5 and -8 is ……….. than -5.
Solution:
(i) An integer, on the given number line, is greater than every number on its left.
(ii) An integer, on the given number line, is greater than every number to its left.
(iii) 2 is greater than – 4 implies 2 is on the right of – 4.
(iv) – 3 is less than 2 and 3 is greater than -2.
(v) – 4 is greater than -8 and 4 is less than 8.
(vi) 5 is greater than 2 and – 5 is less than – 2.
(vii) -6 is less than 3 and the opposite of -6 is greater than opposite of 3.
(viii) 8 is greater than -5 and -8 is less than -5.
Question 2.
In each of the following pairs, state which integer is greater :
(i) -15, -23
(ii) -12, 15
(iii) 0, 8
(iv) 0, -3
Solution:
(i) -15, -23
-15 is greater than -23 as -15 lies on the right side of-23 on the number line
(ii) -12, 15
15 is greater than than -12 as 15 lies on the right side of -12 on the number line
(iii) 0, 8 8 > 0
(iv) 0, -3 0 > – 3
Question 3.
In each of the following pairs, which integer is smaller :
(i) o, -6
(ii) 2, -3
(iii) 15, -51
(iv) 13, 0
Solution:
(i) 0, -6
-6 < 0
(ii) 2, -3
-3 < 2
(iii) 15, -51
-51 < 15
(iv) 13, 0
0 < 13
Question 4.
In each of the following pairs, replace * with < or > to make the statement true:
(i) 3 * 0
(ii) 0 * -8
(iii) -9 * -3
(iv) 3 * 3
(v) 5 * -1
(vi) -13 * 0
(vii) -8 * -18
(viii) 516 * -316
Solution:
(i) 3 > 0
(ii) 0 > -8
(iii) -9 < -3
(iv) -3 < 3
(v) 5 > -1
(vi) -13 < 0
(vii) -8 > -18
(viii) 516 > -316
Question 5.
In each case, arrange the given integers in ascending order using a number line.
(i) – 8, 0, – 5, 5, 4, – 1
(ii) 3, – 3, 4, – 7, 0, – 6, 2
Solution:
(i) – 8, 0, – 5, 5, 4, – 1
Draw a number line and mark the numbers on it. Arranging in ascending order, as shown -8,-5,-1, 0, 4, 5 as on the number line

(ii) 3, -3, 4, -7, 0, -6, 2
Draw the number line and mark the numbers on it. Arranging in ascending order as shown on the number line.
-7, -6, -3, 0, 2, 3, 4

Question 6.
In each case, arrange the given integers in descending order using a number line.
(i) -5, -3, 8, 15, 0, -2
(ii) 12, 23, -11, 0, 7, 6
Solution:
(i) -5, -3, 8, 15, 0, -2
Draw the number line and mark these numbers on it. Arranging in descending order 15, 8, 0 -2, -3, -5 as shown on the number line

(ii) 12, 23, -11, 0, 7, 6
Draw a number line and mark these numbers on it. Arranging in descending order. 23, 12, 7, 6, 0, -1 as shown on the number line

Question 7.
For each of the statements, given below, state whether it is true or false :
(i) The smallest integer is 0.
(ii) The opposite of -17 is 17.
(iii) The opposite of zero is zero.
(iv) Every negative integar is smaller than 0.
(v) 0 is greater than every positive integer.
(vi) Since, zero is neither negative nor positive ; it is not an integer.
Solution:
(i) False
(ii) True
(iii) True
(iv) True
(v) False
(vi) False
Number Line Exercise 7B – Selina Concise Mathematics Class 6 ICSE Solutions
Use a number line to evaluate each of the following :
Question 1.
(i) (+ 7) + (+ 4)
(ii) 0 + (+ 6)
(iii) (+ 5) + 0
Solution:

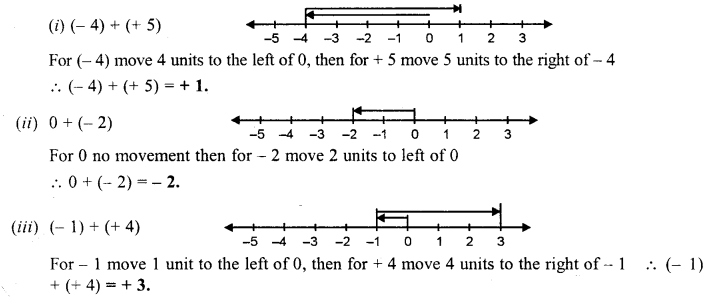
Question 2.
(i) (-4) + (+5)
(ii) 0 + (-2)
(iii) (-1) + (-4)
Solution:
Question 3.
(i) (+ 4) + (-2)
(ii) (+3) + (-6)
(iii) 3 + (-7)
Solution:
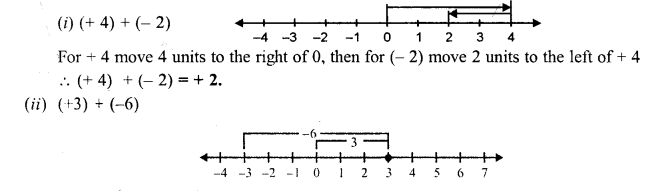

Question 4.
(i) (-1) + (-2)
(ii) (-2) + (-5)
(ii) (-3) + (-4)
Solution:
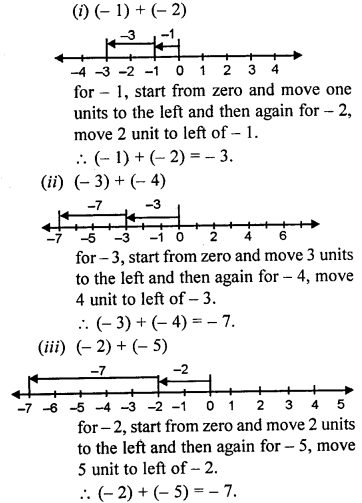
Question 5.
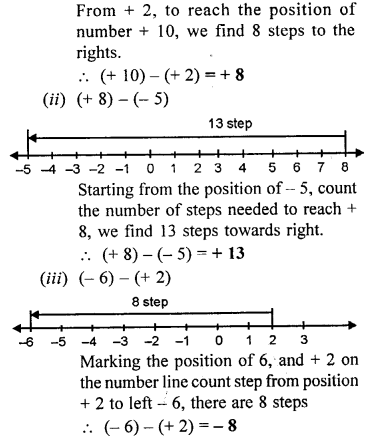
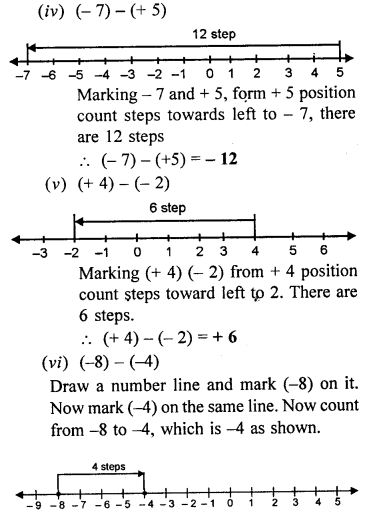
(i) (+ 10) – (+2)
(ii) (+8)- (-5)
(iii) (-6) – (+2)
(iv) (-7) – (+5)
(v) (+4) – (-2)
(vi) (-8) – (-4)
Solution:
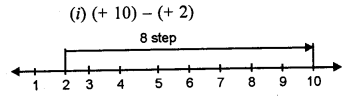
Question 6.
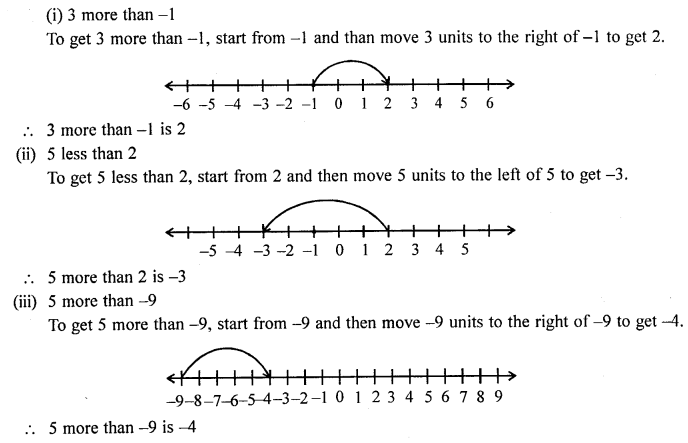
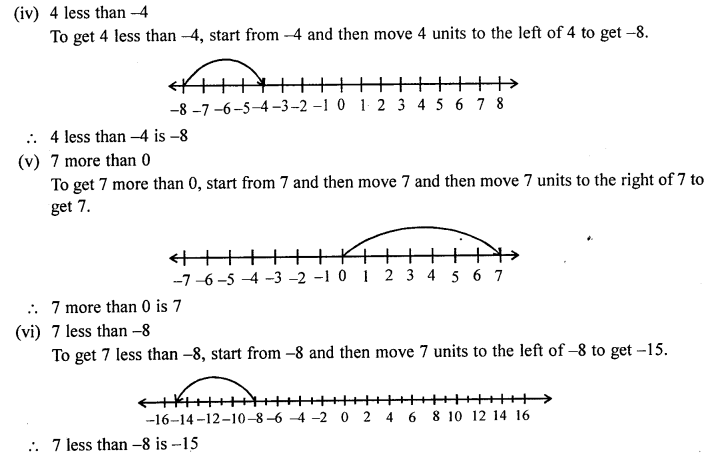
Using a number line, find the integer which is :
(i) 3 more than -1
(ii) 5 less than 2
(iii) 5 more than -9
(iv) 4 less than -4
(v) 7 more than 0
(vi) 7 less than -8
Solution:
Number Line Revision Exercise – Selina Concise Mathematics Class 6 ICSE Solutions
Question 1.
Fill in the blanks :
(i) 5 is …………… than -2 and -5 is ………… than 2.
(ii) -3 is ………… than 0 and 3 is …………. than 0.
(iii) on a number line, if x is to the left of y, then x is ………… than y.
(iv) on a number line if x is to the right of y, then y is …………. than x.
Solution:
(i) 5 is greater than -2 and -5 is less than 2.
(ii) -3 is less than 0 and 3 is greater than 0.
(iii) On a number line, if x is to the left of y, then x is less than y.
(iv) On a number line, x is to the right of y, then y is less than x.
Question 2.
Using a number line, write the numbers -15, 7, 0, -8 and -3 in ascending order of value.
Solution:
On the given number line, we mark the numbers -15, 7, 0, -8 and -3 on it, we see that
![]()
We see that -15 < -8 < -3 < 0 < 7
-15, -8, -3, 0, 7 are in ascending order
Question 3.
Using a number line, write the numbers 8, -6, 2 -12, 0, 15 and -1 in descending order of value.
Solution:
On the given number line, we mark the numbers 8, -6, 2, -12, 0, 15 and -1 on it
![]()
We see that
15 > 8 > 2 > 0 > -1 > -6 > -12
15, 8, 2, 0, -1, -6, -12 are in descending order
Question 4.
Using a number line, evaluate :
(i) (+5) + (+4)
(ii) (+6) + (+8)
(iii) (-3) + (+5)
(iv) (-3) + (+7)
(v) (+6) + (-2)
(vi) (-3) + (+3)
(vii) (-5) + (-5)
(viii) (-7) + (-1)
(ix) (+6) – (+2)
(x) (+5) – (-3)
(xi) (+4) – (-1)
(xii) (-7) – (-2)
Solution:
(i) (+5) + (+4)
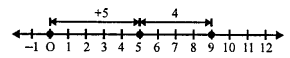
First of all, we move 5 units to the right of zero then for (+4), move 4 units right of 5, then we reach at 9, then
(+5) + (+4) = +9
(ii) (+6) + (+8)

First of all, we move 6 units to the right of zero then for (+8), we move 8 units to the right of (+6)
Then we reach at +14, then
(+6) + (+8) = +14
(iii) (-3) + (+5)
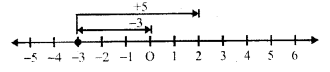
First of all for (-3) we move, 3 units to the left of zero, then move (+5) units to the right of 5, then we reach at (+2), then
(-3) + (+5) = -3 + 5 = 2
(iv) (-3) + (+7)
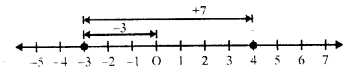
First of all, we move for (-3) 3 unit to the left of zero and then for (+7), we move 7 units to the right of (-3) reaching +4 Then (-3) + (+7) = +4
(v) (+6) + (-2)
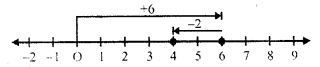
First of all, we move for (+6), 6 units to the right of zero and then for (-2), move 2 units to the left of 6, then we reach 4 Then (+6) + (-2) = 6 – 2 = 4
(vi) (-3) + (+3)
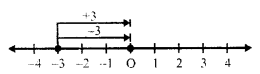
First of all for (-3), we move 3 units left of zero and then for (+3) we move 3 unit right of (-3) reaching at 0
So, (-3) + (+3) = 0
(vii) (-5) + (-5)
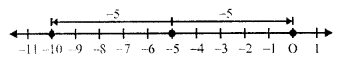
First of all for -5, we move 5 units to left of zero and then for (-5), we move 5 units to left of (-5) reaching at -10
(-5) +(-5) = -10
(viii) (-7) + (-1)
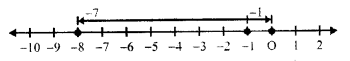
First of all for -7, we move 7 units left of zero and then for (-1) we move 1 unit left of -7 reaching -8
(-7) + (-1) = -8
(ix) (+6) – (+2)
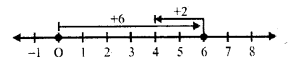
First of all for (+6) we move 6 units right of 0 and then for (+2), we move 2 units left of 6 reaching 4
(+6)-(+2) = 6 – 2 = 4
(x) (+5) – (-3)

Mark the points (+5) and (-3) on the same number line. We see that the position of (-3) is 8 units from (+5) to its right 3.
(+5) – (-3) = 5 + 3 = 8
(xi) (+4) – (-1)
![]()
Mark the points (+4) and (-1) on the same number line, we see that the position of (-1) is 5 units from (+4) to its right
(+4) – (-1) = 4 + 1 = 5
(xii) (-7) – (-2)
![]()
Mark the points (-7) and (-2) on the same number line, we see that (-2) is 5 units on the left (-2)
-7 – (-2) = -7 + 2 = -5