Selina Concise Mathematics Class 6 ICSE Solutions Chapter 8 HCF and LCM

Selina Concise Mathematics Class 6 ICSE Solutions Chapter 8 HCF and LCM

Selina Publishers Concise Mathematics Class 6 ICSE Solutions Chapter 8 HCF and LCM

ICSE SolutionsSelina ICSE SolutionsML Aggarwal Solutions

APlusTopper.com provides step by step solutions for Selina Concise ICSE Solutions for Class 6 Mathematics. You can download the Selina Concise Mathematics ICSE Solutions for Class 6 with Free PDF download option. Selina Publishers Concise Mathematics for Class 6 ICSE Solutions all questions are solved and explained by expert mathematic teachers as per ICSE board guidelines.

Selina Class 6 Maths ICSE SolutionsPhysicsChemistryBiologyGeographyHistory & Civics

IMPORTANT POINTS

Factor of a given number is that number by which the given number can be divided completely.

1. Prime Numbers :
   A Natural number, which is divisible by 1 (one) and itself only is called a prime number.
2. Highest Common Factor :
   H.C.F. stands for Highest Common Factor and H.C.F. of two or more given numbers is the greatest number (factor) which divides each given number completely.
3. Lowest Common Factor :
   L.C.M. stands for Lowest Common Multiple. The L.C.M. of two or more given numbers is the lowest (smallest) number which is exactly divisible by each of the given numbers.

HCF and LCM Exercise 8A – Selina Concise Mathematics Class 6 ICSE Solutions

Question 1.
Write all the factors of :
(i) 15
(ii) 55
(iii) 48
(iv) 36
(v) 84
Solution:
(i) Factors of 15 = F₁₅ = 1, 3, 5 and 15
(ii) Factors of 55 = F₅₅ = 1, 5, 11 and 55
(iii) Factors of 48 = F₄₈ = 1, 2, 3, 4, 6, 8, 12, 16, 24 and 48
(iv) Factors of 36 = F₅₆ = 1, 2, 3, 4, 6, 9, 12, 18 and 36.
(v) Factors of 84 = F₈₄ = 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42 and 84.

Question 2.
Write all prime numbers :
(i) less than 25
(ii) between 15 and 35
(iii) between 8 and 76
Solution:
(i) 2, 3, 5, 7, 11, 13, 17, 19 and 23
(ii) 17, 19, 23, 29 and 31
(iii) 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71 and 73.

Question 3.
Write the prime-numbers from :
(i) 5 to 45
(ii) 2 to 32
(iii) 8 to 48
(iv) 9 to 59
Solution:
(i) 7, 11, 13, 17, 19, 23, 29, 31, 37, 41 and 43.
(ii) 3, 5, 7, 11, 13, 17, 19, 23 29 and 31.
(iii) 11, 13, 17, 19, 23, 29, 31, 37, 41, 43 and 47.
(iv) 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47 and 53.

Question 4.
Write the prime factors of:
(i) 16
(ii) 27
(iii) 35
(iv) 49
Solution:
(i) Prime factors of 16 = 2

(ii) Prime factors of 27 = 3

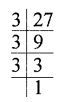
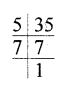
(iii) Prime factors of 35 = 5, 7

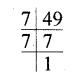
(iv) Prime factors of 49 = 7

Question 5.
If P_n means prime factors of n, find:
(i) p₆
(ii) P₂₄
(iii) p₅₀
(iv) P₄₂
Solution:
(i) F₆ = 1, 2, 3, 6
P.F₆ (Prime factor of 6) = 2 and 3.
(ii) F₂₄ = 1, 2, 3, 4, 6, 8, 12, 24
P.F₂₄ = 2 and 3.
(iii) F₅₀ = 2, 5, 5
P.F₅₀ = 2 and 5.
(iv) F₄₂ = 1, 2, 3, 6, 7, 14, 21, 42
P.F₄₂ = 2, 3 and 7.

HCF and LCM Exercise 8B – Selina Concise Mathematics Class 6 ICSE Solutions

Question 1.
Using the common factor method, find the H.C.F. of :
(i) 16 and 35
(ii) 25 and 20
(iii) 27 and 75
(iv) 8, 12 and 18
(v) 24, 36, 45 and 60
Solution:
(i) F₁₆ = 1, 2, 4, 8, 16
F₃₅ = 1, 5, 7, 35
Common factors between 16 and 35 = 1
H.C.F. of 16 and 35 = 1
(ii) F₂₅ = 1, 5, 25
F₂₀ = 1, 2, 4, 5, 10, 20
Common factors between 25 and 20 = 1, 5
H.C.F. of 25 and 20 = 5
(iii) F₂₇ = 1, 3, 9, 27
F₇₅ = 1, 3, 5, 15, 25, 75
Common factors between 27 and 75 = 1, 3
H.C.F. of 27 and 75 = 3
(iv) F₈ = 1, 2, 4, 8
F₁₂ = 1, 2, 3, 4, 6, 12
F₁₈ = 1, 2, 3, 6, 9, 18
Common factors between 8, 12 and 18 = 1, 2
H.C.F. of 8, 12 and 18 = 2
(v) F₂₄ = 1, 2, 3, 4, 6, 8, 12, 24
F₃₆ = 1, 2, 3, 4, 6, 12, 18, 36
F₄₅ = 1, 3, 5, 9, 15, 45
F₆₀ = 1, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
Common factor between 24, 36, 45 and 60 = 1, 3
H.C.F. of 24, 36, 45 and 60 = 3

Question 2.
Using the prime factor method, find the H.C.F. of:
(i) 5 and 8
(ii) 24 and 49
(iii) 40, 60 and 80
(iv) 48, 84 and 88
(v) 12, 16 and 28
Solution:
(i) Prime factor of 5 = 5
Prime factor of 8 = 2 x 2 x 2
No common prime factor
H.C.F. of 5 and 8 = 1
(as both the number are co-prime)
(ii) Prime factor of 24 = 2 x 2 x 2 x 3
Prime factor of 49 = 7 x 7
No common prime factor, number are co-prime.
H.C.F. of 24 and 49 = 1.
(iii) Prime factor of 40 = 2 x 2 x 2 x 5
Prime factor of 60 = 2 x 2 x 3 x 5
Prime factor of 80 = 2 x 2 x 2 x 2 x 5
Common prime factor = 2 x 2 x 5
H.C.F. of 40, 60 and 80 = 2 x 2 x 5 = 20
(iv) Prime factor of 48 = 2 x 2 x 2 x 2 x 3
Prime factor of 84 = 2 x 2 x 3 x 7
Prime factor of 88 = 2 x 2 x 2 x 11
Common prime factor of 48, 84 and 88 = 2 x 2
H.C.F. of 48, 84 and 88 = 2 x 2 = 4
(v) Prime factor of 12 = 2 x 2 x 3
Prime factor of 16 = 2 x 2 x 2 x 2
Prime factor of 28 = 2 x 2 x 7
Common prime factor between 12, 16 and 28 = 2 x 2
H.C.F. of 12, 16 and 28 = 2 x 2 = 4

Question 3.
Using the division method, find the H.C.F. of the following :
(i) 16 and 24
(ii) 18 and 30
(iii) 7, 14 and 24
(iv) 70,80,120 and 150
(v) 32, 56 and 46
Solution:

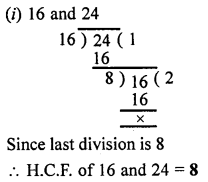
Question 4.
Use a method of your own choice to find the H.C.F. of :
(i) 45, 75 and 135
(ii) 48, 36 and 96
(iii) 66, 33 and 132
(iv) 24, 36, 60 and 132
(v) 30, 60, 90 and 105
Solution:
(i) Factor of 45 = F₄₅ = 3 x 3 x 5
Factor of 75 = F₇₅ = 3 x 5 x 5
and Factor of 135 = F₁₃₅ = 3 x 3 x 3 x 5
Now the common factors of 45, 75 and 135 = 3 and 5
H.C.F. = 3 x 5 = 15
(ii) Factor of 48 = F₄₈ = 2 x 2 x 2 x 2 x 3
Factor of 36 = F₃₆ = 2 x 2 x 3 x 3
and factor of 96 = 2 x 2 x 2 x 2 x 2 x 3
Now the common factor of 48, 36 and 96 = 2, 2 and 3
H.C.F. = 2 x 2 x 3 = 12
(iii) Factor of 66 = F₆₆ = 2 x 3 x 11
Factor of 33 = F₃₃ = 3 x 11
and factor of 132 = F₁₃₂ = 2 x 2 x 3 x 11
Now the common factor of 66, 33 and 132 = 3 and 11
H.C.F. = 3 x 11 =33
(iv) Factor of 24 = F₂₄ = 2 x 2 x 2 x 3
Factor of 36 = F₃₆ = 2 x 2 x 3 x 3
Factor of 60 = F₆₀ = 2 x 2 x 3 x 5
and Factor of 132 = F₁₃₂ = 2 x 2 x 3 x 11
Now the common factors of 24, 36, 60 and 132 = 2, 2 and 3
H.C.F. = 2 x 2 x 3 = 12
(v) Factor of 30 = F₃₀ = 2 x 3 x 5
Factor of 60 = F₆₀ = 2 x 2 x 3 x 5
Factor of 90 = F₉₀ = 2 x 3 x 3 x 5
and factor of 105 = F₁₀₅ = 3 x 5 x 7
Now the common factor of 30, 60, 90 and 105 = 3 and 5
H.C.F. = 3 x 5 = 15

Question 5.
Find the greatest number that divides each of 180, 225 and 315 completely.
Solution:
The greatest number that divides 180, 225 and 315 will be HCF of 180, 225, 315
Let us first find HCF of 180 and 225

Question 6.
Show that 45 and 56 are co-prime numbers.
Solution:
The HCF of two co-prime numbers is always HCF of 45 and 56

Question 7.
Out of 15, 16, 21 and 28, find out all the pairs of co-prime numbers.
Solution:


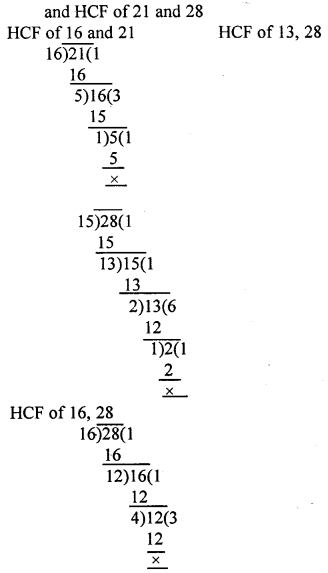
From above it is clear that 15 and 16 are co-prime because common factor is 1
Hence pairs 15 and 16, 16, 21, 15, 28 are co-prime number.

Question 8.
Find the greatest no. that will divide 93, 111 and 129, leaving remainder 3 in each case.
Solution:
Since Remainder is 3 in each case numbers are
93 – 3 = 90
111 – 3 = 108
129 – 3 = 126
Required number will be HCF of90,108 and 126 HCF of 90 and 108

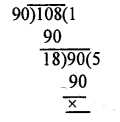
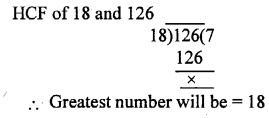
HCF and LCM Exercise 8C – Selina Concise Mathematics Class 6 ICSE Solutions

Question 1.
Using the common multiple method, find the L.C.M. of the following :
(i) 8, 12 and 24
(ii) 10, 15 and 20
(iii) 3, 6, 9 and 12
Solution:

Question 2.
Find the L.C.M. of each the following groups of numbers, using
(i) the prime factor method and
(ii) the common division method :
(i) 18, 24 and 96
(ii) 100, 150 and 200
(iii) 14, 21 and 98
(iv) 22, 121 and 33
(v) 34, 85 and 51
Solution:
(i) L.C.M. of 18, 24 and 96
(i) By prime factors
Prime factors of 18 = 2 x 3 x 3
Prime factors of 24 = 2 x 2 x 2 x 3
Prime factors of 96 = 2 x 2 x 2 x 2 x 2 x 3
L.C.M. = 2 x 2 x 2 x 2 x 2 x 3 x 3 = 288
By common division method
L.C.M. of 18, 24 and 96 = 2 x 2 x 2 x 3 x 3 x 4 = 288

Question 3.
The H.C.F. and the L.C.M. of two numbers are 50 and 300 respectively. If one of the numbers is 150, find the other one.
Solution:
H.C.F. = 50
L.C.M. = 300
Product of L.C.M. and H.C.F. = 300 x 50 = 15000
One number = 150
The other number

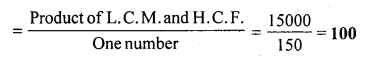
Question 4.
The product of two numbers is 432 and their L.C.M. is 72. Find their H.C.F.
Solution:
Product of two numbers = Product of their L.C.M. and H.C.F.
Here, product of two number = 432
L.C.M. = 72
H.C.F. = \(\frac { 432 }{ 72 }\) = 6

Question 5.
The product of two numbers is 19,200 and their H.C.F. is 40. Find their L.C.M.
Solution:

Question 6.
Find the smallest number which, when divided by 12, 15, 18, 24 and 36 leaves no remainder
Solution:
The least number which is exactly divisible by each given number is their L.C.M.
Required number L.C.M. of 12, 15, 18, 24 and 36.

Question 7.
Find the smallest number which, when increased by one is exactly divisible by 12, 18, 24, 32 and 40
Solution:

Question 8.
Find the smallest number which, on being decreased by 3, is completely divisible by 18, 36, 32 and 27.
Solution:
LCM of 18, 36, 32 and 27

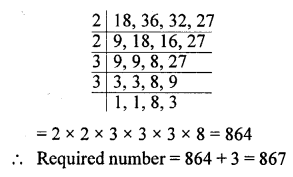
HCF and LCM Revision Exercise – Selina Concise Mathematics Class 6 ICSE Solutions

Question 1.
Find the H.C.F. of :
(i) 108, 288 and 420
(ii) 36, 54 and 138
Solution:
(i) H.C.F. of 108, 288, 420 = 12

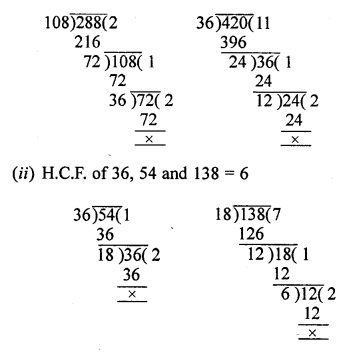
Question 2.
Find the L.C.M. of:
(i) 72, 80 and 252
(ii) 48, 66 and 120
Solution:
L.C.M. 72, 80, 252

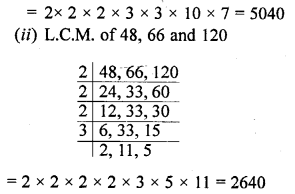
Question 3.
State true or false : Give an example.
(i) H.C.F. of two prime numbers is 1.
(ii) H.C.F. of two co-prime numbers is 1.
(iii) L.C.M. of two prime numbers is equal to their product.
(iv) L.C.M. of two co-prime numbers is equal to their product.
Solution:
(i) True : Because the prime numbers have no common factor except 1.
(ii) True : Becuase co-prime numbers have no common factor except 1.
(iii) True : Because the prime number have no common factor except 1.
(iv) True : Because co-prime numbers have no common factor except 1.

Question 4.
The product of two numbers is 12096 and their H.C.F. is 36. Find their L.C.M.
Solution:
We know that
Product of two numbers = Product of their H.C.F. and L.C.M.
=> 12096 = 36 x L.C.M.
=> L.C.M. = \(\frac { 12096 }{ 36 }\) = 336

Question 5.
The product of the H.C.F. and the L.C.M. of two numbers is 1152. If one number is 48, find the other one.
Solution:
We know that:
Product of two numbers = Product of their H.C.F. and L.C.M.
=> 1st number x 2nd number = Product of their H.C.F. and L.C.M.
=> 48 x 2nd number = 1152
=> 2nd number = \(\frac { 1152 }{ 48 }\) = 24

Question 6.
(i) Find the smallest number that is completely divisible by 28 and 42.
(ii) Find the largest number that can divide 28 and 42 completely.
Solution:
(i) We know that the least number which is divisible by 28 and 42 is their L.C.M.

L.C.M. of 28 and 42 = 2 x 2 x 3 x 7 = 84
(ii) We know that the largest number which can divide 28 and 42 completely will be their H.C.F.

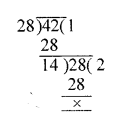
H.C.F. of 28 and 42 = 14

Question 7.
Find the L.C.M. of 140 and 168. Use the L.C.M. obtained to find the H.C.F. of the given numbers.
Solution:
Numbers are 140 and 168
L.C.M. of 140 and 168

Question 8.
Find the H.C.F. of 108 and 450 and use the H.C.F. obtained to find the L.C.M. of the given numbers.
Solution:
Numbers are given : 108 and 450
H.C.F. of 108 and 450= 18

Selina Class 6 Maths ICSE SolutionsPhysicsChemistryBiologyGeographyHistory & Civics