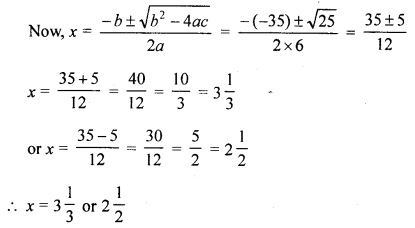Selina Concise Mathematics Class 10 ICSE Solutions Revision Paper 5
Section A (40 Marks)
(Answer all questions from this Section)
Question 1.
(a) An article was purchased by a distributor for ₹ 15,000. He sold it to a trader for ₹ 20,000. The trader sold the article to a retailer for ₹ 22,000. Find the VAT paid by the distributor and the trader if the tax rate was 10%.
(b) The maturity value of a cumulative deposit account is ₹ 31,800 in 2 years. If the rate of interest is 10% per annum, find the monthly instalment of this deposit.
(c) Find how many terms of the series 17 + 15 + 13 + …… must be added to get sum equal to 72?
Solution:
(a) C.P. of an article = ₹^15000
SP of the article = ₹ 20000
Cost price for the trader = ₹ 20000
S.P. for the trader or C.P. for the retailer = ₹ 22000
Rate of VAT = 10%

∴ VAT paid to govt. = ₹ 2200 – ₹ 2000 = ₹ 200
(b) Maturity value = 31800
Period (n) = 2 years = 24 months
Rate of interest (r) = 10%
Let p be the monthly deposit
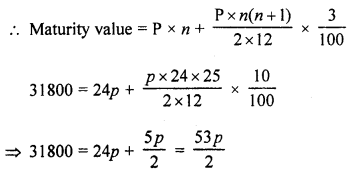
∴ \(\mathrm{P}=\frac{31800 \times 2}{53}\) = ₹ 1200
∴ Monthly deposit = ₹ 1200
(c) A.P. is 17 + 15 + 13 + …….
Sum = 72, a = 17, d= 15 – 17 =-2
Let n be the number of terms be added
∴ Sn= \(\frac{n}{2}\) [2a + (n- 1)d]
⇒ 72= \(\frac{n}{2}\) [2 × 17 + (n – 1) × (-2)]
⇒ 72 × 2 = n(34 – 2n + 2)
⇒ 144 = n(36-2n)
⇒ 144 = 36n – 2n2
⇒ 2n2 – 36n+ 144
⇒ n2 – 18n + 72 = 0
⇒ n2 – 6n – 12n + 72 = 0
⇒ n(n – 6) – 12(n – 6) = 0
⇒ (n – 6) (n – 12) = 0
Either n – 6 = 0, then w = 6 or n – 12 = 0, then n = 12
∴ Number of terms = 6 or 12
Question 2.
(a) What number should be added to 27x3 – 54x2 + 36x – 11 so that the resulting polynomial becomes divisible by 3x – 2 ?
(b) If P (9a – 2, -b) divides the line segment joining the points A (3a + 1, -3) and B (8a, 5) in the ratio 3 : 1; find the values of a and b.
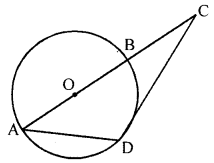
(c) In the given figure, AB is a diameter and DC is tangent which meets AB produced at point C. If angle ∠DAC = x°, find in terms of x° :
(i) ∠DCB
(ii) ∠DBC
Solution:
(a) Let f(x) = 27x3 – 54x2 + 36x – 11
Dividing by 3x – 2
We get remainder = -3
∴ The required number when added to f(x) = (-3) = 3
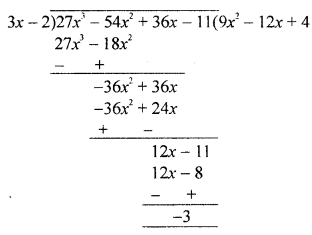
(b) Point P (9a – 2, -b) divides the line segment joining point A (3a + 1, -3) and B (8a, 5) in the ratio 3 : 1
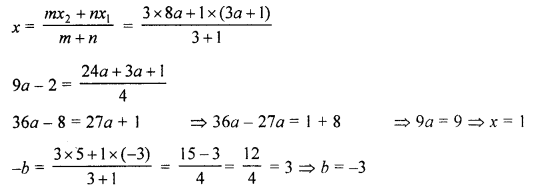
∴ a = 1, b = -3
(c) In the given figure,
AB is diameter, DC is tangent to the circle with centre O which meets AB produced at point C ∠DAC = x°
To find : ∠DCB and ∠DBC
Join BD.
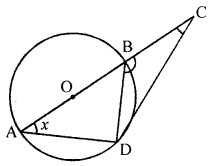
∠ADB = 90° (Angle in a senicircle)
In ∆ADB
Ext. ∠DBC = ∠BAD + ∠ADB
= x + 90° or 90° + x
∠BDC = ∠BAD = x
In ∆BDC,
∠DCB = 180° – (BDC + DBC)
= 180° – (x + 90° + x)
= 180° – 90° – 2x = 90° – 2x
Question 3.
(a) Prove that the locus of a point equidistant from the extremities a line segment is the perpendicular bisector of it.
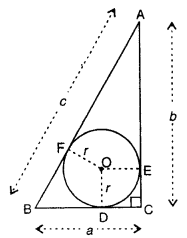
(b) If a, b and c are sides of a right triangle where c is the hypotenuse, prove that the radius of the circle which touches the sides of the triangle is r = \(\frac{a+b-c}{2}\).
(c) If between two numbers one geometric mean is G and two arithmetic means are p and q, prove that: G2 = (2p – q) (2q – p).
Solution:
(a) Given : Two fixed points A and B
P is the moving point PA = PB. Join AB.
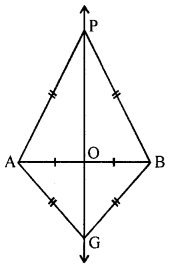
To prove : Locus of point P lies on the perpendicular line which is equidistant from A and B i.e., PA = PB
Proof: In ∆AOP and ∆BOP
AO = OB (O is mid-point of AB)
PA = PB (given)
PO = PO (common)
∴ ∆AOP ~ ∆BOP (SSS axiom)
∴ P lies on the perpendicular bisector of AB.
(b) In the figure, a, b, c are the sides of a right triangle, c is hypotenuse.
A incircle is drawn with radius r
To prove : r = \(\frac{a+b-c}{2}\)
Construction : Join OA, OB and OC
Proof: ∴ ∠C = 90°
∴ ∠DOE is a square whose each side is equal to the radius of the circle = r
Now BF = BD = BC – DC = a – r
and AF = AE = AC – EC = b – r
∴ AB = BF + AF = a – r + b – r
c = a-r + b- r ⇒ c = a + b – 2r
⇒ 2r = a + b – c
\(r=\frac{a+b-c}{2}\)
Hence proved.
(c) G is geometric mean between a, b
∴ G2 = ab
p and q are AM between a and b
∴ p – a = q – p ⇒ 2p = a + q
⇒ a = (2p – q) ….(i)
and q – p = b – q ⇒ b = 2q – p …..(ii)
Now, G2 = ab = (2p – q) (2q – p) [From (i) and (ii)]
Hence proved.
Question 4.
(a) Find x, if : sin 47° sec 43° + cos 43° cosec 47° – x cos2 45° = 0.
(b) A (8, 0), B (0, -8) and C (-16, 0) are the vertices of a triangle ABC. If P is in AB and Q is in AC such that AP : PB = AQ : QC = 3 : 5; show that: 8 PQ = 3 BC.
(c) Find the value of x, if the mean of the following distribution is 18.
| Data | 13 | 15 | 17 | 19 | 20 + x | 23 |
| Frequency | 8 | 2 | 3 | 4 | 5x | 6 |
Solution:
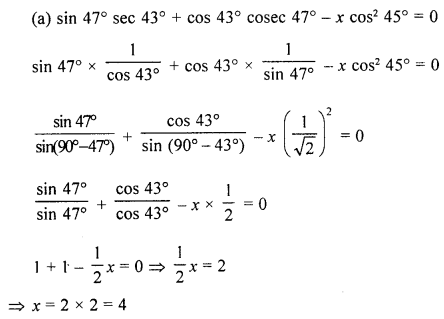
(b) In ∆ABC, vertices are A (8, 0), B (0, -8), C (-16, 0) P and Q are points on the sides AB and AC such that AP : PB = AQ : QC = 3:5
Join PQ
Prove that 8 PQ = 3 BC
Ratio in AP : PB and AQ : QC = 3:5
∴ Co-ordinates of P will be
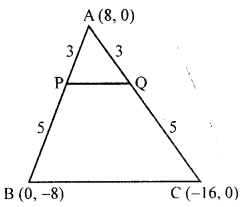

Hence Proved
(c)
Date (x) | Frequency (f) | fx |
| 13 | 8 | 104 |
| 15 | 2 | 30 |
| 17 | 3 | 51 |
| 19 | 4 | 76 |
| 20 + x | 5x | 100x + 5x2 |
| 23 | 6 | 138 |
| Total | 23 + 5x | 399 + 100 x + 5x2 |
Mean = \(\frac{\sum f x}{\Sigma f}\)
∴ 18 = \(18=\frac{399+100 x+5 x^{2}}{23+5 x}\)
⇒ 5x2 + 100x + 399 = 414 + 90x
⇒ 5x2 + 100x – 90x + 399 – 414 = 0
⇒ 5x2 + 10x – 15 = 0
⇒ x2 + 2x – 3 = 0
⇒ x2 + 3x – x – 3 = 0
⇒ x(x + 3) – 1 (x + 3) = 0
⇒ (x + 3) (x – 1) = 0
Either x + 3 = 0, then x = -3 which is-not possible as x cannot be negative or x – 1 =0, then x = 1
Hence, x = 1
Sections B (40 Marks)
(Answer any four questions from this Section)
Question 5.
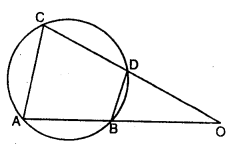
(a) In the given figure, chords AB and CD of the circle are produced to meet at O. Prove that triangles ODB and OCA are similar. Give that CD = 2 cm, DO = 6 cm and BO = 3 cm,
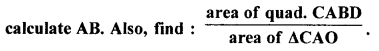
(b) If M × \(\left[\begin{array}{cc}{3} & {2} \\ {2} & {-1}\end{array}\right]=\left[\begin{array}{cc}{-1} & {4}\end{array}\right]\); find:
(i) the order of matrix M.
(ii) the matrix M.
(c) The diameter of a closed cylinder is 7 cm and its height is 16 cm. Find :
(i) the lateral surface area of the cylinder.
(ii) the total surface area of the cylinder.
(iii) the volume of the cylinder. [Take π = \(3 \frac{1}{7}\)]
Solution:
(a) In the given figure, chord AB and CD of a circle meet each other at O on producing. AC and BD are joined.
To prove :
(i) ∆ODB ~ ∆OCA
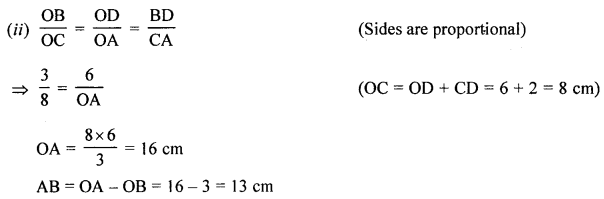
(ii) If CD = 2 cm, DO = 6 cm and BO = 3 cm, calculate AB
(iii) Find \(\frac{\text { area of quad. CABD }}{\text { area } \Delta \mathrm{CAO}}\)
Proof:
(i) In ∆ODB and ∆OCA
∠O = ∠O (Common)
Ext. ∠DBO = ∠ACD (in cylic quad. ABCD)
∴ ∆ODB ~ ∆OCA (AA axiom)
(iii) ∵ Triangles ODB and OCA are similar
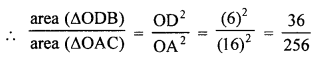
[The ratio of the areas as of two similar triangles is equal to the ratio of the squares of any two corresponding sides.]
Subtracting both sides from 1, we get

We know that the product of matrices is possible only when the number of columns in the first matrix is equal to the number of rows in the second.
∴ b = 2
and also the number of rows of product matrix is equal to the number of rows of the first matrics
∴ a = 1
∴ Order of matrix M = a × b = 1 × 2
Let M= [x y]
\(\therefore\left[\begin{array}{ll}{x} & {y}\end{array}\right] \times\left[\begin{array}{cc}{3} & {2} \\ {2} & {-1}\end{array}\right]=\left[\begin{array}{cc}{-1} & {4}\end{array}\right]\)
[3x + 2y 2x – y] =[-1 4]
Comparing, we get
3x + 2y = -1 …(i)
2x – y = 4 ⇒ y = 2x – 4 ………..(ii)
Substituting the value of y in (i)
3x + 2(2x – 4) = -1
3x + 4x – 8 = -1 ⇒ 7x = -1 + 8 = 7
∴ x = \(\frac{7}{7}\) = 1
and y = 2x – 4 = 2 × 1 – 4 = 2 – 4 = -2
∴ M= [1 -2]
(c) Diameter of closed cylinder = 7 cm
∴ Radius (r) = \(\frac{7}{2}\) cm
and height (h) = 16 cm
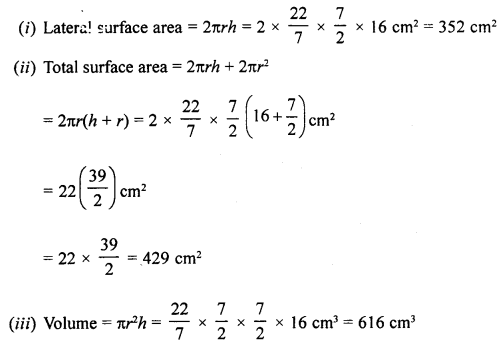
Question 6.
(a) From a point of observation at the top of a 175 m high cliff, the angles of depression of two objects are x° and y° such that tan x° = 2.5 and tan y° = 1.4. If the point of observation and the two objects are along the same straight line, find the distance between the two objects if they are on the :
(i) same side of the cliff
(ii) opposite sides of the cliff.
(b) If P (x, y) is any point on the line joining the points A (a, 0) and B (0, b), then show that :
\(\frac{x}{a}+\frac{y}{b}=1\)
(c) Show that, if A = \(\left[\begin{array}{ll}{1} & {3} \\ {2} & {6}\end{array}\right] \text { and } \mathbf{B}\left[\begin{array}{cc}{-1} & {4} \\ {2} & {1}\end{array}\right]\) then: : (A + B)2 ≠ A2 + 2AB + B2
Solution:
(a) Let AB be a cliff 175 m high
Let C and D are two objects which makes angle of depressions of x° and y°.
tan x° = 2.5 and tan y° = 1.4
We have to find the distance between there two objects, if
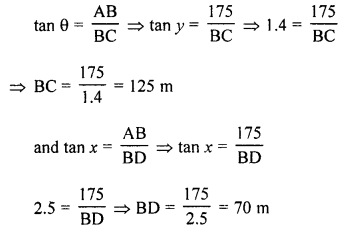
If C and D are on the same side [see figure (i)]
CD = BC – BD = 125 – 70 = 55 m
If C & D are in opposite direction [see figure (ii)]
CD = BC + BD = 125 + 70 = 195 m
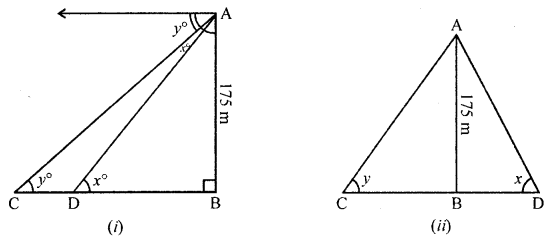
(b) Points are A (a, 0), B (0, b)
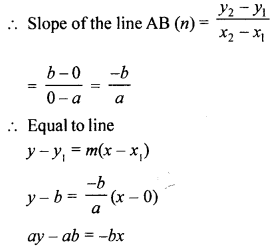
bx + ay = ab
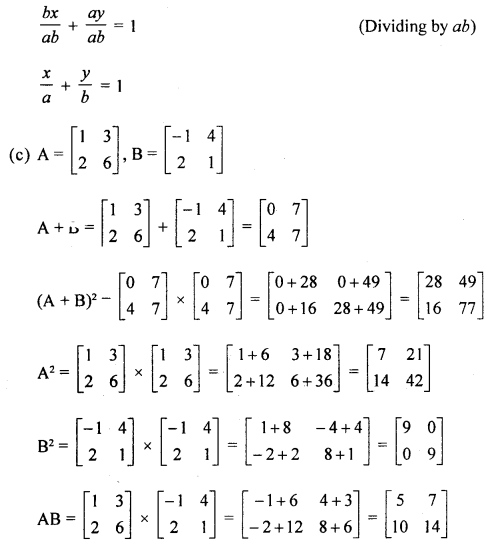

Question 7.
(a) Angles of the same segment of a circle are equal prove it.
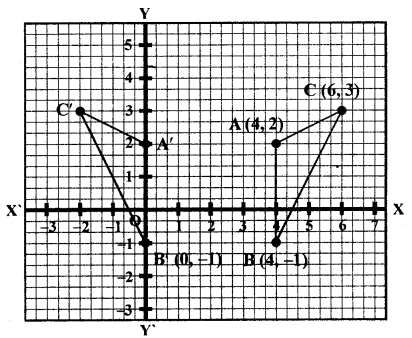
(b) On a graph pape# plot the triangle ABC whose vertices are at the points A (4, 2), B (4, -1) and C (6, 3). On the same graph, draw the image of the triangle ABC under reflection in the line x = 2. Mark any two points on the graph paper which are invariant under this reflection. Also, write the co-ordinates of points marked.
(c) The point P divides the join of (2, 1) and (-3, 6) in the ratio 2 : 3. Does P lie on the line x – 5y + 15 = 0 ?
Solution:
(a) In a circle, with centre O, ∠ABC and ∠ADC are in the same segment.
To prove : ∠ABC = ∠ADC
Construction : Join OA and OC.
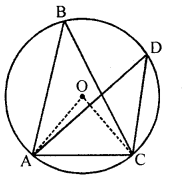
Proof: v arc AC subtends ∠AOC on the centre of the circle and ZABC on the remaining part of the circle.
∴ ∠AOC = 2∠ABC …..(i)
Similarly ∠AOC = 2∠ADC …(ii)
From (i) and (ii),
2∠ABC = 2∠ADC
⇒ ∠ABC = ∠ADC
(b) We have plotted the points A (4, 2), B (4, -1) and C (6, 3) on the graph.
Draw a line x = 2
∆A’B’C’ is the image of ∆ABC
Co-ordinates of A’, B’ and C’ are (0, 2), (0, -1) and (-2, 3) respectively under reflection, every point which lies on the x = 2, is in variant.
Some points are (2, 0), (2, 3), (2, -5), etc.
(c) Point P divides the line joining the points (2, 1), (-3, 6) in the ratio 2 : 3
Let co-ordinates of P be (x, y)
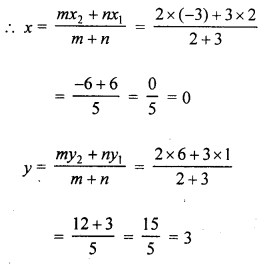
∴Co-ordinates of P are (0, 3)
Substituting the value of x and y in the equation
x – 5y + 15 = 0
L.H.S. 0 – 5 × 3 + 15
= 0 – 15 + 15 = 0 = R.H.S.
Hence point P lies on the given line x – 5y+ 15 = 0
Question 8.
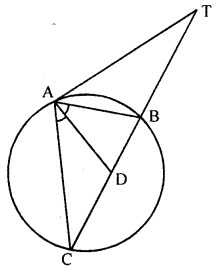
(a) In the adjoining figure, TA is a tangent to the circle and TBC is a secant. If AD bisects angle BAC, prove that: ∠ADT = ∠TAD and ∠ADT is isosceles.
(b) The ends of a diagonal of a square have co-ordinates (-2, p) and (p, 2). Find p, if the area of the square is 40 sq. units.
(c) I have shares of three companies A, B and C in the ratio 2 : 3 : 4. Company A pays 20% dividend when its ₹ 250 share is available for ₹ 310. Company B pays 18% dividend when its ₹ 100 share is available in the market for ₹ 112. Company C pays 15% dividend when its ₹ 50 share is available in the market for ₹ 43. If on the whole, I earn ₹ 55,200 as dividend from these shares, find the number of shares of each company that I have and the total market value of these shares.
Solution:
(a) In the given figure, TA is tangent to the circle and TBC is a secant.
AD bisects ∠BAC.
To prove : ∠ADT = ∠TAD
∆ADT is an isosceles triangle
Proof: AD is the bisector of ∠CAB
∴ ∠1 = ∠2
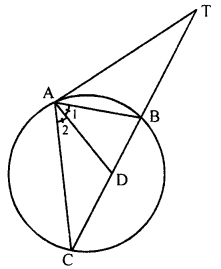
AT is tangent and AB is chord
∴ ∠AB = ∠C (Angles in alternate segment)
∴ ∠1 + ∠TAB = ∠2 + ∠C
But Ext. ∠ADT = ∠2 + ∠C (in ZACD)
⇒ ∠TAD – ∠ATD
or ∠ATD = ∠TAD
∆ADT is an isosceles triangle
(b) In square ABCD, co-ordinates of ends of diagonal AC are (-2, p) and (p, 2)
Area of square = 40 sq. units
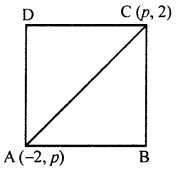
∴ Side = \(\sqrt{40}\) units
and length of diagonal = \(\sqrt{40}\) × Side
= \(\sqrt{2} \times \sqrt{40}=\sqrt{80}\) units = \(4 \sqrt{5}\) units
But length of diagonal AC = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
(c) Ratio in the shares of three company A, B, C = 2 : 3 : 4
Let shares of A company = 2x
Shares of B company = 3x
and shares of C company = 4x
Total dividend from the company’s shares = ₹ 55200
In company A, shares 2x
Face value of each share = ₹ 250
Market value = ₹ 310
Dividend = 20%

∴ Number of shares of A company = 2x = 2 × 300 = 600
Number of shares of B company = 3x = 3 × 300 = 900
and number of shares of C company = 4x = 4 × 300 = 1200
Now investment to A’company = 600 × 310 = ₹ 186000
Investment to B company = 900 × 112 = ₹ 100800
Investment to C company = 1200 × 43 = ₹ 51600
Total investment = ₹ 186000 + ₹ 100800 + ₹ 51600 = ₹ 338400
Question 9.
(a) Tickets numbered from 1 to 20 are mixed up together and then a ticket is drawn at random. What is the probability that the ticket has a number, which is a multiple of 3 or 5 ?
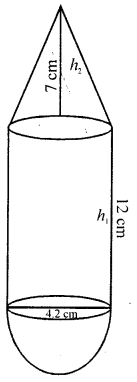
(b) A solid is in the form of a right circular cylinder with a hemispherical shape at one end and a cone at the other end. Their common diameter is 4.2 cm and the heights of the cylindrical and conical portions are 12 cm and 7 cm respectively. Find the volume of the solid.
(c) The surface area of a solid metallic sphere is 1256 cm2. It is melted and recast into solid right circular cones each of radius 2.5 cm and height 8 cm. Find the number of cones formed [Take π = 3.14].
Solution:
(a) Tickets numbered from 1 to 20
Mixed together and one ticket is drawn at random.
∴ Total number of outcomes = 20
Probability of a number which is a multiple of 3 or 5
(3, 5, 6, 9, 10, 12, 15, 18, 20) = 9
∴ Probability P(E) = \(\frac{9}{20}\)
(b) A solid is formed with a hemispherical shape at one end of cylinder and cone on other end
Diameter = 4.2 cm
∴ Radius = \(\frac{4.2}{2}\) =2.1 cm
Height of cylinder = 12 cm and height of cone = 7 cm
∴ Total volume of the solid


Question 10.
(a) The marks obtained (out of 100) by 400 students in an examination are given below :
| Marks | No. of students | Marks | No. of students |
| 0-10 | 10 | 50-60 | 76 |
| 10-20 | 20 | 60-70 | 80 |
| 20-30 | 22 | 70-80 | 58 |
| 30-40 | 40 | 80-90 | 28 |
| 40-50 | 54 | 90-100 | 12 |
Using a graph paper, draw an ogive for the above distribution. Use your ogive to estimate:
(i) the median.
(ii) the number of students who obtained more than 80% marks in the examination.
(iii) the number of students who did not pass, if the pass percentage was 35.
(b) If 49 – 5x ≤ 27 – X, find :
(i) the smallest value of x, when x is a real number.
(ii) the smallest value of x, when x is an integer.
Solution:
(a)
| Marks | Number of students (f) | c.f. |
| 0-10 | 10 | 10 |
| 10-20 | 20 | 30 |
| 20-30 | 22 | 52 |
| 30-40 | 40 | 92 |
| 40-50 | 54 | 146 |
| 50-60 | 76 | 222 |
| 60-70 | 80 | 302 |
| 70-80 | 58 | 360 |
| 80-90 | 28 | 388 |
| 90-100 | 12 | 400 |
Plot the points (10, 10), (20, 30), (30, 52), (40, 92), (50, 146), (60, 222), (70, 302), (80, 360), (90, 388) and (100, 400) on the graph and join them in free hand to get an ogive as shown.
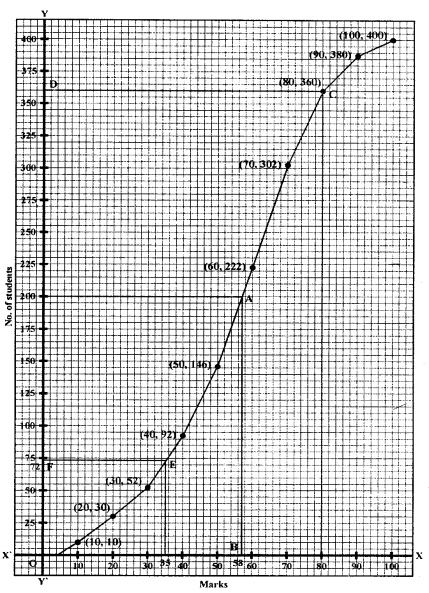
Total number of students = 400
∴ \(\frac{n}{2}=\frac{400}{2}=200\)
From 200 ony-axis draw a line parallel to x-axis meeting curve at A and from A, draw a perpendicular to x-axis meeting at B which 58 marks.
From 80 on x-axis draw a line perpendicular to x-axis which meets the curve at C and from C, draw a line parallel to x-axis meeting y-axis at 360.
∴ Number of students getting more than 80% marks = 400 – 360 = 40
Similarly from 35 on x-axis draw a line parallel toy-axis meeting the curve at E and from E draw a line parallel to x-axis meeting y-axis at F which is 72.
Hence number of students get less than 35% marks i.e., below pass marks = 72
(b) 49 – 5x ≤ 27 – x
⇒ 49 – 27 ≤ -x + 5x
⇒ 22 ≤ 4x
⇒ 4x ≥ 22
⇒ \(x \geq \frac{22}{4} \Rightarrow x \geq 5.5\)
(i) When x is a real number, then x = 5.5
(ii) When x is an integer, then x = 6
Question 11.
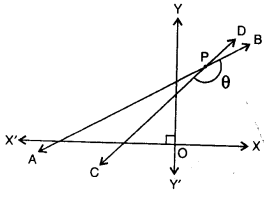
(a) The figure drawn alongside (not drawn to scale) shows two straight lines AB and CD. If the equation of line AB is :
x – \(\sqrt{3}\)x + 5 = 0 and the equation of line Cd is : x – y = 2; write down the inclinations of lines AB and CD; also find the angle θ i.e., angle CPB.
(b) (i) If cosec θ . cos (θ + 54°) = 1, find the value of θ so that θ and (θ + 54°) are acute angles.
(ii) If tan 4θ = cot 5θ, find θ. Given 4θ and 5θ both are acute.
(c) Solve using formula : 6x2 – 35x + 50 = 0
Solution:
(a) In the given figure, two straight lines AB and CD equation of AB is x – \(\sqrt{3} y\) + 5 = 0 and of CD is x – y = 2
Slope of line AB

∴ Angle of inclination = 30°
and slope of CD
x – y = 2 ⇒ y = x – 2
Slope = 1 i.e., tan 45°
∴ Angle of inclination = 45°
In ∆APC,
Ext. ∠ACP = 180° – 45° = 135°
and Ext. BPC = ∠A + ∠ACD
= 30° + 135° = 165°
θ = 165°
(b) (i) cosec θ. cos (θ + 54°) = 1