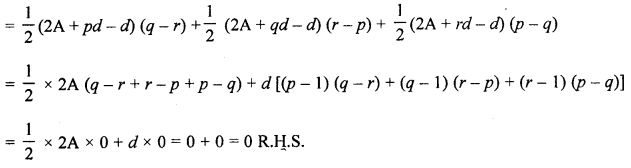Selina Concise Mathematics Class 10 ICSE Solutions Revision Paper 3
Section A (40 Marks)
(Answer all questions from this Section)
Question 1.
(a) A man invested ₹ 9,000 in 3% (₹ 100) shares at a discount of 10%. He sold all the shares at the rate of ₹ 95 each and invested the proceeds in 4% (₹ 50) shares at par. Find the change in his income.
Solution:
Investment = ₹ 9000 in 3% ₹ 100 shares at discount of 10%
∴ Number of shares purchased = \(\frac{9000}{90}\) = 100
Dividend = 100 × 3 = ₹ 300
By selling them at ₹95
Sale proceed = ₹ 95 × 100 = ₹ 9500
By investing them at par (₹ 50) shares
Dividend = 9500 × \(\frac{4}{100}\) = ₹ 380
Increase in income = ₹ 380 – ₹ 300 = ₹ 80
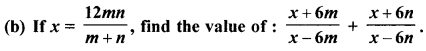
Solution:

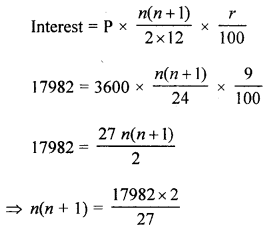
(c) Find the sum of the terms of the sequence : 5 + 8 + 11 + ……… + 68.
Solution:
Sum of the terms 5 + 8 + 11 + ……. + 68
Here, a = 5, d = 8 – 5 = 3, l = 68
l = Tn = a + (n – 1)d ⇒ 68 = 5 + (n – 1) (3)
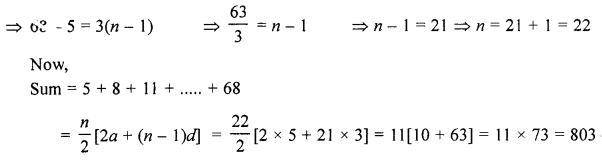
Question 2.
(a) Use the factor theorem to factorize x3 + x2 – 4x – 4 completely.
Solution:
f(x) = x3 + x2 – 4x – 4
Factor of -4 = 1, -1, 2, -2, 4, -4
x = -1, then
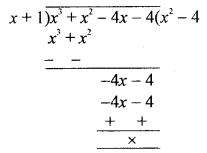
f(-1) = (-1)3 + (-1)2 – 4(1) – 4
= -1 + 1+ 4 – 4 = 0
∴ x + 1 is a factor of f(x)
Dividing by x + 1, we get
f(x) = (x + 1) (x2 – 4) = (x + 1) {(x)2 – (2)2}
= (x + 1) (x + 2) (x – 2)
(b) A die is thrown two times and the total score in two throws is noted. Find the probability that the total score is :
(i) an even number
(ii) 6
(iii) at least 6.
Solution:
A die is thrown two times
∴ Total outcomes = 6 × 6 = 36
(i) An even number
Probability of an even number = \(\frac{18}{36}\) (out of 36, 18 are odd, 18 are even)
= \(\frac{1}{12}\)
(ii) Total score = 6 which can be
1 + 5, 2 + 4, 3 + 3, 4 + 2, 5 + 1= 5
∴ Probability =\(\frac{5}{36}\)
(iii) At least sum = 6
Which can be 36 – 10 = 26
(Ten are 1 + 1, 1 + 2, 1 + 3, 1 + 4, 1 + 5, 2 + 1, 2 + 2, 2 + 3, 3 +1, 3 + 2 = 10)
∴ Probability = \(\frac{26}{36}=\frac{13}{18}\)
(c) In the given figure, lenths of arcs APB and BQC are in the ratio 5 : 3 and angle AOC = 152°; find angle ACB and angle BAC.
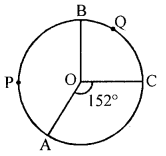
Solution:
In the given figure,
Ratio in the lengths of arcs APB and BQC = 5 : 3
∠AOC = 152°
To find : ∠ACB and ∠BAC
Join AC, BC and AB
Ratio in arc APB and arc BQC = 5 : 3
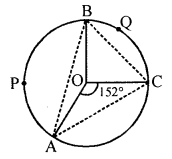
and ∠AOB + ∠BOC = 360° – 152° = 208°

Question 3.
(a) A cummulative deposit account of monthly instalment of ₹ 3,600 at 9% p.a. simple interest earns an interest of ₹ 17,982. Find the number of instalments paid.
Solution:
Monthly instalment = ₹ 3600
Rate of interest = 9% p.a.
Total interest = 17982
Let number of instalments = n
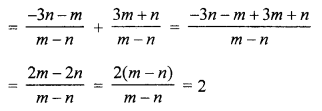
n2 + n = 1332
⇒ n2 + n – 1332 = 0
⇒ n2 + 37n – 36n – 1332 = 0
⇒ n(n + 37) – 36(n + 37) = 0
⇒ (n + 37) (n – 36) = 0
Either (n + 37) = 0, then n = -37 which is not possible being negative,
or n – 36 = 0, then n = 36
∴ Number of instalment = 36
(b) A cylindrical vessel of diameter 14 cm and height 42 cm is fixed symmetrically inside a similar vessel of radius 8 cm and height 42 cm. The total space between the two vessels is fill with glass-wool for heat insulation. Find the volume of the glass-wool required.
Solution:
Diameter of inner cylinder = 14 cm
Radius (r) = \(\frac{14}{2}\) = 7 cm
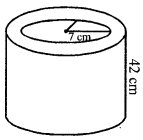
and height (h) = 42 cm
Radius of outer cylinder (R) = 8 cm
Height (h) = 42 cm
The space (volume) between the two cylinders
= πh[R2 – r2]
= \(\frac{22}{7}\) × 42(82 – 72) cm3
= 132(8 + 7) (8 -7) cm3
= 132 × 15 × 1 = 1980 cm3
(c) On a graph paper plot the triangle ABC whose vertices are at points A (5, 4), B (7, 5) and C (-3, 6). On the same graph, draw the image of the triangle ABC under reflection in the liney = 3. Mark any two points on the graph paper which are invariant under this reflection. Also, write the co-ordinates of points marked.
Solution:
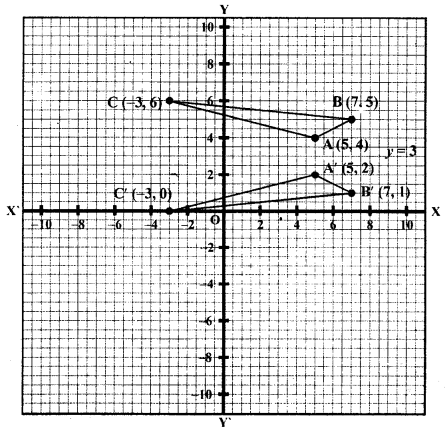
Plot the points on the graph A (5, 4), B (7, 5), C (-3, 6). Join them to get a triangle ABC.
The image of AABC in the line y = 3 is AA’B’C’ as shown.
The co-ordinates of A’ are (5, 2), B’ (7, 1)and C’ (-3, 0)
There are many points on x = 3, (invariant points)
These points can be (-5, 3), (-2, 3), (0, 3) (4, 3), etc.
Question 4.
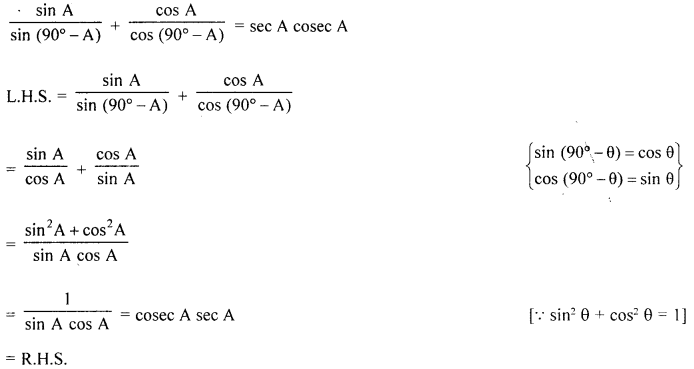
(a) Prove that : 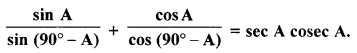
Solution:
(b) Find the ratio in which the two co-ordinate axes divide the line segment joining the points (-2, 5) and (1, -9).
Solution:
Let the line joining the points (-2, 5) and (1,-9) is divided by the x-axis in the ratio m : n, then
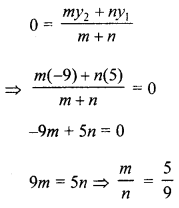
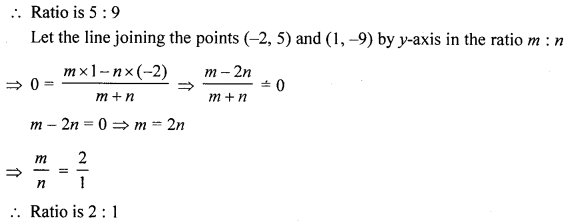
(c) Use short-cut method to find the mean of monthly wages of a certain number of workers:
| Monthly wages (in ₹) | 90-110 | 110-130 | 130-150 | 150-170 | 170-190 |
| No. of workers | 4 | 6 | 4 | 8 | 18 |
Find the new mean, when :
(i) the monthly wage of each worker is increased by 30%.
(ii) the number of workers in each category is halved.
(iii) the number of workers in each category is doubled and the monthly wage in each category is decreased by 20%.
Solution:
| Monthly wages | Mid value (x) | Frequency (f) | A = 140 d = x – A | fd |
| 90-110 | 100 | 4 | -40 | -160 |
| 110-130 | 120 | 6 | -20 | -120 |
| 130-150 | 140 | 4 | 0 | 0 |
| 150-170 | 160 | 8 | 20 | 160 |
| 170-190 | 180 | 18 | 40 | 720 |
| Total | 40 | 600 |
Mean = \(\mathrm{A}+\frac{f d}{\Sigma f}\)
= 140+ \(\frac{600}{40}\) = 140+ 15 = ₹ 155 40
(i) New mean when each worker gets 30% increased wages
= ₹ 155 × \(\frac{130}{100}=\frac{2015}{10}=201.50\)
∵ Wages of every worker is increased by 30%
∵ Mean will also be increased by 30%
(ii)
| Monthly wages | Mid value (x) | f(Half) | fx |
| 90-110 | 100 | 2 | 200 |
| 110-130 | 120 | 3 | 360 |
| 130-150 | 140 | 2 | 280 |
| 150-170 | 160 | 4 | 640 |
| 170-190 | 180 | 9 | 1620 |
| Total | 20 | 3100 |
New mean = \(\frac{3100}{20}=155\)
(iii) Workers of each catagory is doubled and monthly wages is decreased by 20%
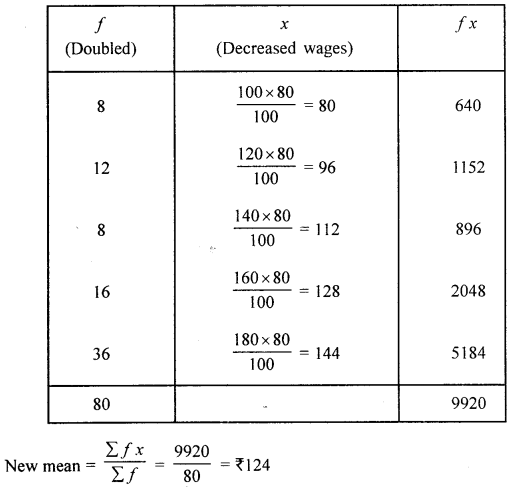
Section B (40 Marks)
(Answer any four questions from this Section)
Question 5.
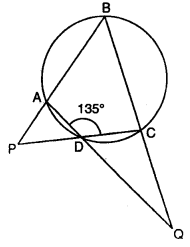
(a) ABCD is a cyclic quadrilateral with ∠ADC = 135°. Sides BA and CD produced meet at point P, sides AD and BC produced meet at point Q. If ∠P : ∠Q = 2 : 1; find angles P and Q.
Solution:
In the given figure,
ABCD is a cyclic quadrilateral with ∠ADC = 135°
Sides BA and CD are produced to meet at P and sides AD and BC are produced to meet at Q.
Also, ∠P : ∠Q = 2 : 1
To find the angles P and Q
Proof: ∠ADC = 135°
∴ ∠ADP = ∠CDQ = 180° – 135° = 45°
Ext. ADC = ∠PAD + ∠P = ∠QCD + ∠Q = 135°
Adding, ∠PAD + ∠P + ∠QCD + ∠Q = 135° + 135° = 270°
But ∠PAD + ∠QCD = 180°
∴ ∠P + ∠Q = 270° – 180° = 90°
But ∠P = ∠Q ⇒ ∠P : ∠Q = 2 : 1
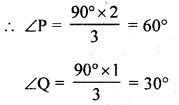
(b) A right circular cone is 3.6 cm high and radius of its base is 1.6 cm. It is melted and recast into a right circular cone with radius of the base as 1.2 cm. Find the height.
Solution:
Height of a right circular cone (h) = 3.6 cm
and radius of its base (r) = 1.6 cm

(c) In G.P. 2, 6, 18, 54,………., 13122; the product of 3rd term from the beginning and 3rd term from the last is 26244. Show it.
Solution:
G.P. 2, 6, 18, 54, …….., 13122
Product of 3rd term from the beggining and 3rd from the last term is 26244

Question 6.
(a) A manufactures an articles and sells it to B for ₹ 30,000. B sells it to C at a profit of ₹ 4,000 and C sells it to D at a profit of ₹ 6,000. If the rate of sales-tax is 10%, find the total amount of VAT paid to the government and the price paid by D.
Solution:
A’s selling price for an articles = ₹ 30000
B sells it to C at a profit of ₹ 4000
S.P. for C = ₹ 30000 + ₹ 4000 = ₹ 34000
C sells it to D for a profit of ₹ 6000
= ₹ 34000 + ₹ 6000 = ₹ 40000
Rate of sales tax = 10%
∴ VAT which D paid to govenment = ₹ 40000 × \(\frac{10}{100}\) = ₹ 4000
Total price paid by D = ₹ 40000 + ₹ 4000 = ₹ 44000
(b) Is the line through (-2, 3) and (4, 1) perpendicular to the.line 3x = y + 1 ?, Does the line 3x = y + 1 bisect the join of (-2, 3) and (4, 1) ?
Solution:
3x = y+ 1 ⇒ y = 3x – 1
∴ Slope (m1) = 3
Slope of line joining the points (-2, 3) and (4, 1)
\(m_{2}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{1-3}{4+2}=\frac{-2}{6}=\frac{-1}{3}\)

Hence line 3x = y+ 1 bisects the line joining the points (-2, 3) and (4, 1)
(c) If the roots of the equation (b – c)x2 + (c – a)x + (a – b) = 0 are equal, prove that 2b = a + c.
Solution:
Roots of (b – c)x2 + (c – a)x + (a – b) = 0 are equal
∴ B2 – 4AC = (c – a)2– 4(b -c) (a – b)
= c2 + a2 – 2ca – 4(ab – b2 – ca + bc)
= c2 + a2 – 2ca – 4ab + 4b2 + 4ca – bc
= a2 + 4b2 + c2 – 4ab + 2ac + 4be
∵ Roots are equal B2 – 4AC = 0
a2 + 4b2 + c2 – 4ab – 2ac – 4bc = 0
⇒ (a – 2b + c)2 = 0
a – 2b + c = 0 ⇒ a + c = 2b
∴ 2b = a + c
Question 7.
(a) In a positive fraction, the denominator is greater than the numerator by 3. If 1 is subtracted from both the numerator and the denominator, the fraction is decreased by \(\frac{1}{14}\). Find the fraction.
Solution:
Let number of a fraction = x
Then denominator = x + 3
∴ Fraction \(=\frac{x}{x+3}\)
According to the condition,
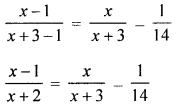
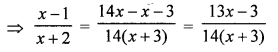
⇒ 14(x + 3)(x – 1) = (13x – 3)(x + 2)
⇒ 14(x2 – x + 3x – 3) = 13x2 + 26x – 3x – 6
⇒ 14x2 – 14x + 42x – 42 = 13x2 + 26x – 3x – 6
⇒ 14x2 – 14x + 42x – 42 – 13×2 – 26x + 3x + 6 = 0
⇒ x2 + 5x – 36 = 0
⇒ x2 + 9x – 4x – 36 = 0
⇒ x(x + 9) – 4(x – 9) = 0
⇒ (x + 9)(x – 4) = 0
Either x + 9 = 0, then x = -9 which is negative or x – 4 = 0, then x = 4
∴ Fraction = \(\frac{x}{x+3}=\frac{4}{4+3}=\frac{4}{7}\)
(b) Solve : (x2 – 3x)2 – 16(x2 – 3x) – 36 = 0.
Solution:
(x2 – 3x)2 – 16(x2 – 3x) – 36 = 0
Let x2 – 3x = a, then
a2– 16a -36 = 0
⇒ a2 – 18a + 2a -36 = 0
a(a -18) + 2(a – 18) = 0
(a – 18) (a + 2) = 0
Either a – 18 = 0, then a = 18 or a + 2 = 0, then a = -2
(i) When a = 18, then
x2 – 3x = 18 ⇒ x2 – 3x – 18 = 0
⇒ x2 – 6x + 3x – 18 = 0
⇒ x(x – 6) + 3(x – 6) = 0
⇒ (x – 6) (x + 3) = 0
Either x – 6 = 0, then x = 6
or x + 3 = 0, then x = -3
When a = -2, then
x2 – 3x = -2 ⇒ x2 – 3x + 2 = 0
x2 – x – 2x + 2 = 0
x(x – 1) – 2(x – 1) = 0
(x – 1) (x – 2) = 0
Either x – 1 =0, then x = 1 or x – 2 = 0, then x = 2 Hence, x = 1, 2,-3, 6
(c) If -5 is a root of the quadratic equation 2x2 + mx = 15 and the quadratic equation m(x2 + x) + k = 0 has equal roots, find the value of k.
Solution:
-5 is a root of the quadratic equation
2x2 + mx = 15
∴ 2x2 + mx – 15 = 0
⇒ 2(-5)2 + m(-5) -15 = 0
⇒ 50 – 5m = 15 ⇒ 5m = 50 – 15
⇒ -5m = 35 ⇒ m = \(\frac{35}{-5}\) = -7
and m(x2 + x) + k = 0 has equal roots
∴ mx2 + mx + k = 0
⇒ b2 – 4ac = (-m)2 – 4 × m × k = 0
⇒ m2 – 4m × k = 0
⇒ m2 – 4mk = 0 (m = -7)
⇒ (-7)2 – 4(-7)k = 0
⇒ 49 + 28k = 0 ⇒ 28k = -49
⇒ k = \(\frac{-49}{28}=\frac{-7}{4}=-1 \frac{3}{4}\)
Question 8.
(a) There are three containers of equal capacity and all are completely filled with mixtures of acid and water in different ratios, the ratio of acid to water in the first container is 2 : 3, in the second container the ratio is 3 : 7 and in the third container it is 4 : 11. If the mixtures of all the three containers are mixed together, what will be the ratio of acid to water in it ?
Solution:
There are three containers of equal capacity.
Let container be A, B and C and let each is of 30 litres capacity.
∴ In first container, ratio of acid and water is = 2 : 3

∴ In three containers, total capacity of acid =12 + 9 + 8 = 29l
and water = 18 + 21 +22 = 61 l
∴ Ratio of acid and water = 29 : 61
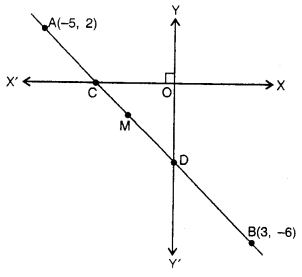
(b) A straight line passes through the points A (-5, 2) and B (3, -6). It intersects the coordinate axes at points C and D as shown in the given diagram. M is a point on AB which divides CD in the ratio 1 : 2. Find :
(i) the equation of AB.
(ii) the co-ordinates of points C and D.
(iii) the co-ordinates of point M.
Solution:
A line passing the points A (-5, 2) and B (3, -6) intersects x-axis at C and y-axis at D. M is the points which divides CD in the ratio 1 : 2
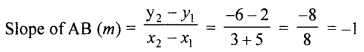
∴ Equation of line AB
y – y2 = m(x – x2)
y + 6 = -1(x – 3) ⇒ y + 6 = -x + 3
x + y + 6 – 3 = 0⇒x + y + 3 = 0
∵ Co-ordinate of C is 0, then y = 0
Then x + 0 + 3 = 0 ⇒ x = -3
and abscissa of D is 0, then x = 0
o + y + 3 = o ⇒ y = -3
∴ Co-ordinates of C are (-3, 0) and of D (0, -3)
Let co-ordinates of M be (x, y)
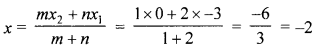
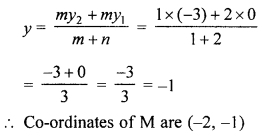

Solution:

Question 9.
(a) Calculate the ratio in which the line joining A (5, 6) and B (-3, 4) is divided by x = 2. Also, find the point of intersection.
Solution:
Let x = 2 divide the line joining the points A (5, 6) and B (-3, 4) in the ratio m : n
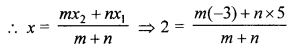
⇒ 2m + 2n = -3m + 5n
2m + 3m = 5n – 2n
⇒ 5m = 3n

(b) A motor boat, whose speed is 15 km per hour in still water, goes 30 km downstream and comes back in a total of 4 hours 30 minutes. Find the speed of the stream.
Solution:
Let the speed of stream = x km/hr
and speed of motor boat = 15 km/h
∴ Speed up stream = (15 – x) km/h
And down stream = (15 + x) hr
According to the condition,
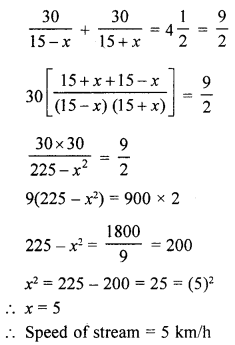
(c) Prove that : sin A (1 + tan A) + cos A (1 + cot A) = sec A + cosec A.
Solution:
sin A (1 + tan A) + cos A (1 + cot A) = sec A + cosec
L.H.S. = sin A (1 + tan A) + cos A (1 + cot A)
= sin A + sin A tan A + cos A + cos A cot A
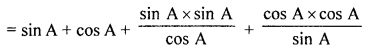

Question 10.
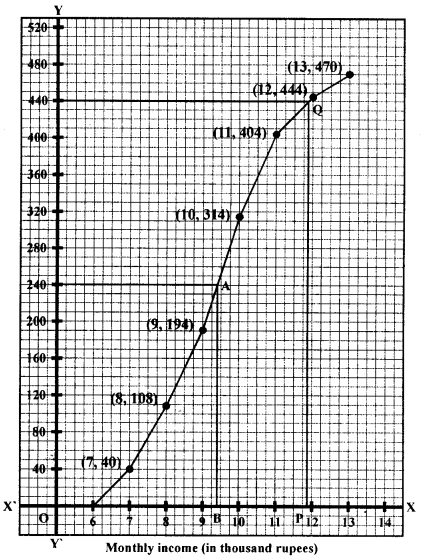
(a)
| Monthly income (in ₹ thousand) | 6-7 | 7-8 | 8-9 | 9-10 | 10-11 | 11-12 | 12-13 |
| No. of workers | 40 | 68 | 86 | 120 | 90 | 40 | 26 |
Draw an ogive for the given data and from it, determine :
(i) the median income.
(ii) the number of employees whose income exceeds ₹ 11,800.
[Take 2 cm = ₹ 1,000 on one axis and 2 cm = 50 employees on the other].
Solution:
| Monthly income (in thousands) | Frequency (No. of workers) | c.f. |
| 6-7 | 40 | 40 |
| 7-8 | 68 | 108 |
| 8-9 | 86 | 194 |
| 9-10 | 120 | 314 |
| 10-11 | 90 | 404 |
| 11-12 | 40 | 444 |
| 12-13 | 26 | 470 |
Plot the points (7, 40), (8, 108), (9, 194), (10, 314), (11, 404), (12, 444), (13, 470) on the graph and join them in free hand to get an ogive as shown below (graph on next page):
(i) Total c.f. = 470
Median =\(\frac{470}{2}\) =235
∴ From 235 on y-axis draw a line parallel to x-axis which meets the curve at A. From A, draw a perpendicular on x-axis which meets it at B.
B is the required median which is ₹ 9350
(ii) No. of employees whose income exceeds ₹ 11800
= 470 – 435 = 35 (approx)
(c) The figure alongside shows a circle with centre O. Chord ED is parallel to diameter AC and angle CBE = 64°. Find angle CED.
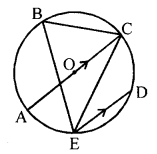
Solution:
In the given figure, a circle with centre O. AC is diameter and ED || AC.
∠CBE = 64°
To find ∠CED
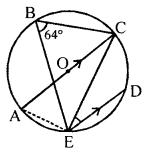
Join DE
∠EAC = ∠EBC = 64° (Angles in the same segment)
In ∆AEC,
∠AEC = 90°
∴ ∠ACE = 180°- (90°+ 64°)
= 180°- 154° = 26°
∵ AC || ED
∴ ∠CED = ∠ACE (Alternate angles)
= 26°
Question 11 :
(a) The sum of 3rd and 11th terms of an A.P. is 34. Find the sum of its 13 terms.
Solution:
Let a be the first term and d be the common difference.
T3 = (a + 2d) and T11 = (a + 10d)
But T3 + T11 = 34
⇒ a + 2d + a + 10d = 34
⇒ 2a+ 12d= 34
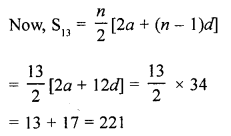
(b) The following table gives marks obtained (out of 25) by 71 students of Class X :
| Marks obtained | 20 | 15 | 17 | 30 | 22 | 25 |
| No. of students | 15 | 7 | 10 | 9 | 17 | 13 |
Find the median marks obtained.
Solution:
| Marks | No. of students (f) | c.f |
| 15 | 7 | 1 |
| 17 | 10 | 17 |
| 20 | 15 | 32 |
| 22 | 17 | 49 |
| 25 | 13 | 62 |
| 30 | 9 | 71 |
No. of students = 71 which is odd
Median = \(\frac{71}{2}\) = 35.5th term = 22
(c) If the sums of p, q and r terms of an A.P. are a, b and c respectively; prove that :
\(\frac{a}{p}(q-r)+\frac{b}{q}(r-p)+\frac{c}{r}(p-q)=0\)
Solution:
Let A be the first term and d be the common difference of an A.P.