Selina Concise Mathematics Class 10 ICSE Solutions Mixed Practice Set B
Question 1.
A retailer buys an article, from a wholesaler, at a discount of 15% on the printed price. He marks up its printed price by 10%. Due to competition in the market, he allows a discount of 5% to the buyer. If the buyer pays ₹ 6,771.60 for the article inclusive of 8% VAT, find :
(i) the printed price of the article,
(ii) the proft percent of the retailer.
(iii) VAT paid by the retailer.
Solution:
Let the marked price of an article = Rs. x
Discount = 15%
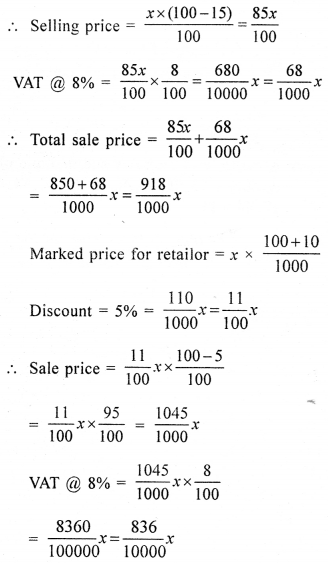
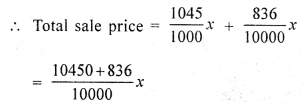
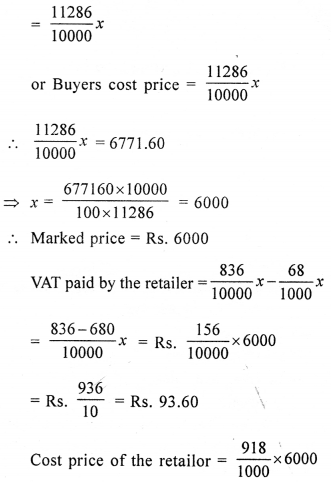
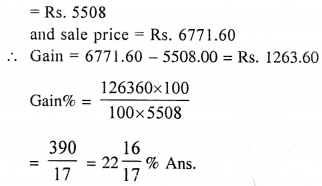
Question 2.
The monthly instalment of a recuring deposit account is ₹ 2.400. If the account is held for 1 year 6 months and its maturity value is ₹ 47,304, fnd the rate of interest.
Solution:
Monthly deposit = ₹ 2400
Period (n) = 1 year 6 months
∴ Total Principal for 1 month
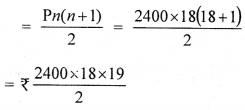
= 2400 × 9 × 19
= ₹ 410400
∴ Maturity value = ₹ 47304
and actual principal = 2400 × 18 = ₹ 43200
∴ Interest = ₹ (47304 – 43200)
= ₹ 4104
Let rate of interest = r% p.a.
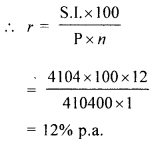
Question 3.
The maturity value of a recurring deposit account is ₹ 42,400. If the account is held for 2 years and rate of interest is 10% per annum, find the amount of each monthly instalment.
Solution:
Maturity value = ₹ 42400
Period (n) = 2 years = 24 months
Rate of interest (r) = 10% p.a.
Let monthly instalment of recurring deposit = ₹ v
∴ Interest = ₹ (42400 – x × 24)
= ₹ 42400 – 24x ……………(i)

⇒ 5x = 84800 – 48x
48x + 5x = 84800
53x = 84800
x = \(\frac{84800}{53}\)
x = ₹ 1600
∴ Monthly instalment = ₹ 1600
Question 4.
A man invests equal amount of money in two companies A and B. Company A pays a dividend of 15% and its T 100 shares are available at 20% discount. The shares of company B has a nominal value of ₹ 25 and are available at 20% premium. If at the end of one year, the man gets equal dividends from both the companies, find the rate of dividend paid by company B.
Solution:
Let in each type of investment = ₹ 100
In the company,
Face value of each share = ₹ 100

∴ Rate of dividend = 22.5%
Question 5.
A sum of ₹ 54,000 is invested partly in shares paying 6% dividend at 40% premium and partly in 5% shares at 25% premium. If the nomial value of one share in each company is ₹ 100 and the total income of the man is ₹ 2,240, find the money invested in the second company.
Solution:
Total investment = ₹ 54000
Let amount invested in first kind of shares = x
∴ Amount invested in second kind of shares = 5400 – x
In first kind of shares
Rate of dividend = 6%
M. V. = 100 + 40 = ₹ 140
N. V. = ₹ 100
∴ Income = \(\frac{x \times 6}{140}=\frac{3 x}{70}\)
In second kind of shares
Rate of dividend = 5%
M. V. = 100 + 25 = 125
N. V. = ₹ 100
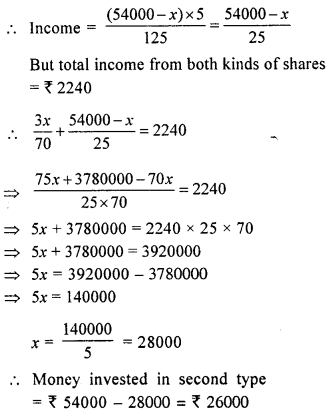
Question 6.
Solve and graph the solution set of :
(i) 2x – 9 < 7 and 3x + 9 ≤ 25; x ϵ R.
(ii) 3x – 2 > 19 or 3 – 2x ≥ – 7; x ϵ R.
Solution:
(i) 2x – 9 < 7 and 3x + 9 ≤ 25; x ϵ R.
2x < 7 + 9 and 3x ≤ 25 – 9 ⇒ 2x < 16 and 3x ≤ 16
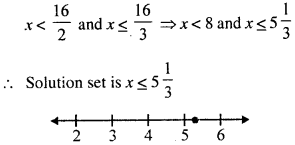
(ii) 3x – 2 > 19 or 3 – 2x ≥ – 7
⇒ 3x > 19 + 2 or -2x ≥ -7 – 3
⇒ 3x > 21 or -2x ≥ -10
∴ x > 7 or – x ≥ – 5
∴ x > 7 or x ≤ 5
![]()
Question 7.
Use formula to solve the quadratic equation x2 + x – (a + 1) (a + 2) = 0.
Solution:
x2 + x – (a + 1) (a + 2) = 0
Here a = 1, b = 1 and c = -(a + 1) (a + 2) = -(a2 + 3a + 2)
∴ D = b2 – 4ac
= (1)2 – 4 × {-(a2 + 3a + 2)}
= 1 + 4(a2 + 3a + 2)
= 1 + 4a2 + 12a + 8
= 4a2 + 12a + 9 = (2a + 3)2
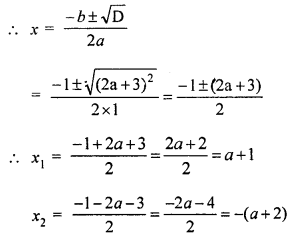
Question 8.
By selling an article for ₹ 96, a man gains as much percent as its cost price. Find the cost price of the article.
Solution:
S.P. of an article = ₹ 96
Let C.P. of the article = ₹ x
∴ Gain = x%
\(\therefore \text { S.P. }=\frac{\mathrm{CP}(100+g a i n \%)}{100}\)
\(96=\frac{x(100+x)}{100}\)
⇒ .x(100 + x) = 9600
⇒ 100x + x2 -9600 = 0
⇒ x2 +100x – 9600 = 0
⇒ x2 + 160x – 60x – 9600 = 0
⇒ x (x + 160) – 60 (x + 160) = 0
⇒ (x + 160) (x – 60) = 0
Either x + 160 = 0, then x = -160 which is not possible
i.e. x – 60 = 0, then x = 60
∴ cost price = ₹ 60
Question 9.
A trader bought a number of articles for ₹ 900, five were damaged and he sold each of the rest at ₹ 2 more than what he paid for it. It on the whole he gains ₹80, find the number of articles bought.
Solution:
Let number of articles = x
C.P. of x articles = ₹ 900

∴ S.P. = ₹ 900 + 80 = ₹ 980
\(\therefore \frac{(x-5)(900+2 x)}{x}=980\)
⇒ 900x + 2x2 – 4500 – 10x = 980x
⇒ 2x2 + 890x – 4500 – 980x = 0
⇒ 2x2 – 90x – 4500 = 0
⇒ x2 – 45x – 2250 = 0
⇒ x2 – 75x + 30x – 2250 = 0
⇒ x(x – 75) + 30(x – 75) = 0
⇒ (x – 75) (x + 30) = 0
Either x – 75 = 0, then x = 75 or x + 30 = 0, then x = -30 which is not possible.
∴ Number of articles purchased = 75
Question 10.
1077 boxes of oranges were loaded in three trucks. While unloading them, 7, 12 and 8 boxes were found rotten in the trucks respectively. If the number of remaining boxes in the three trucks are in the ratio 4 : 6 : 5, find the number of boxes loaded originally in each truck.
Solution:
Total boxes in original =1077
Ratio in the remaining boxes = 4 : 6 : 5
Let boxes unloaded in first truck = 4x
in second truck = 6x
and in third truck = 5x
∴ Number of boxes loaded in the first trucks = 4x + 7
in second truck = 6x + 12
and in third truck = 5x + 8
Now 4x + 7 + 6x + 12 + 5x + 8 = 1077
⇒ 15x + 21 = 1077
15x = 1077 -27
⇒ 15x = 1050
⇒ \(x=\frac{1050}{15}=70\)
∴ Number of boxes loaded in the first truck
= 70 × 4 + 7 = 280 + 7 = 287
Number of boxes in the second truck
= 70 × 6 + 12
= 420 + 12 = 432
and in the third truck
= 70 × 5 + 8
= 350 + 8 = 358
Question 11.
If a ≠ b and a : b is the duplicate ratio of (a + c) and (b + c), show that a, c and b are in continued proportion.
Solution:
∵ a : b is the duplicate ratio of (a + c) and (b + c)
∴ \(\frac{(a+c)^{2}}{(b+c)^{2}}=\frac{a}{b}\)
⇒ b(a + c)2 = a(b + c)2
⇒ b(a2 + c2 + 2ac) = a(b2 + c2+ 2bc)
⇒ a2b + bc2 + 2abc = ab2 + c2a + 2ab2
⇒ a2b + bc2 + 2abc – 2abc = ab2 + c2a
⇒ a2b + bc2 = ab2 + c2a
⇒ c2a – bc2 = a2b – ab2
⇒ c2(a – b) – ab (a – b)
⇒ c2 = ab (∵ a ≠ b)
\(\frac{a}{c}=\frac{c}{b}\)
Hence a, ec and b are in continued proportion.
Question 12.
If \(16\left(\frac{a-x}{a+x}\right)^{3}=\left(\frac{a+x}{a-x}\right)\) show that a = 3x
Solution:
\(16\left(\frac{a-x}{a+x}\right)^{3}=\left(\frac{a+x}{a-x}\right)\)
⇒ 16 [(a – x)3 (a – x)] = (a + x) (a – x)3
⇒ 16 [(a – x)4] = [(a + x)4]
⇒ (2)4 (a – x)4 = (a + x)4
We get,
⇒ 2 (a – x) = a + x
⇒ 2a – 2x = a + x
⇒ 2a – a = x + 2x
∴ a = 3x
Hence proved.
Question 13.
Solve for x, using the properties of proportionality \(\frac{1+x+x^{2}}{1-x+x^{2}}=\frac{62(1+x)}{63(1-x)}\)
Solution:
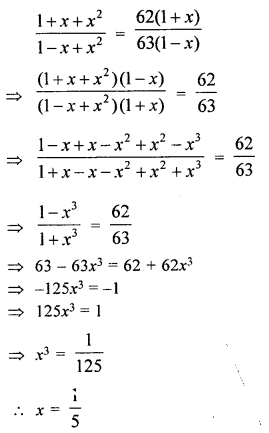
Question 14.
Shows that (2x + 7) is a factor of 2x3 + 7x2 – 4x – 14. Hence, solve the equation : 2x3 + 7x2 – 4x – 14 = 0.
Solution:
Let f(x) = 2x3 + 7x2 – 4x – 14 and 2x + 7 = 0
⇒ 2x = -7
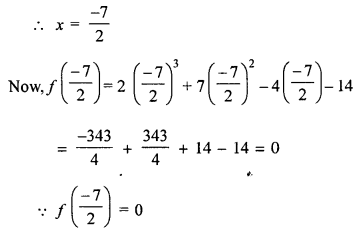
∴ Remainder is zero
Hence 2x + 7 is a factor f(x)
Now dividing f(x) by 2x + 7, we get
Quotient = x2 – 2
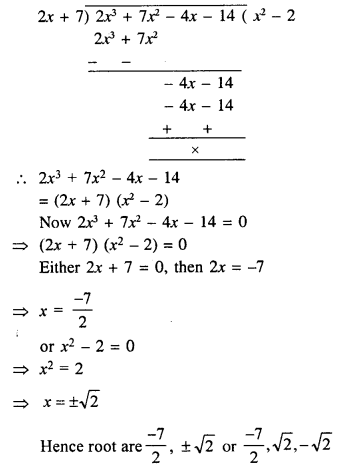
Question 15.
(i) What number should be subtracted from 2x3 – 5x2 + 5x + 8 so that the resulting polynomial has a factor 2x – 3 ?
(ii) The expression 4x32 – bx2 + x – c leaves remainders 0 and 30 when divided by (x + 1) and (2x – 3) respectively. Calculate the values of b and c. Hence, factorise the expression completely.
Solution:
Let f(x) = 2x3 – 5x2 + 5x + 8
and 2x – 3 = 0,
∴ 2x = 3
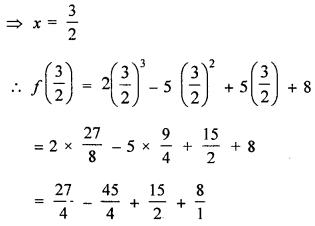
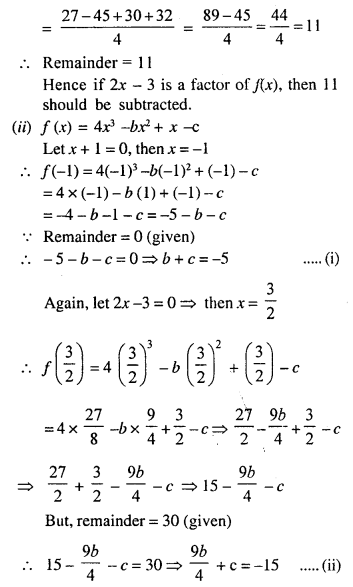

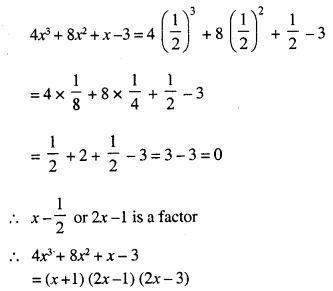
Question 16.
If for two matrices M and N, N = \(\left[\begin{array}{cc}{3} & {2} \\ {2} & {-1}\end{array}\right]\) and product M × N = [-1 4]; find matrix M.
Solution:
Let the order of matrix M be a × b
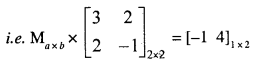
Since, the product of matrices is possible only when the number of columns in the first matrix is equal to the number of rows in the second
∴ b = 2
Also, the number of rows of product (resulting matrix) is equal to the number of rows of first matrix
∴ a = 1 ⇒ order of matrix
M = a × b = 1 × 2
Let M = [r y]
\([x y]\left[\begin{array}{cc}{3} & {2} \\ {2} & {-1}\end{array}\right]=\left[\begin{array}{ll}{-1} & {4}\end{array}\right]\)
⇒ [3x + 2y – 2x – y] = [-1 4]
⇒ 3x + 2y = -1 ….(i)
and 2x – y = 4 ……(ii)
From eq. (i)
\(x=\frac{-1-2 y}{3}\) …(iii)
Put the value of equation (iii) in equation (ii) We get,
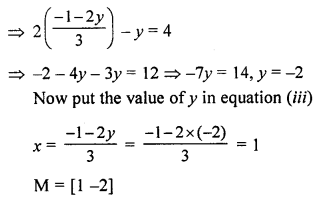
Question 17.
If the sum of first 20 terms of an A.P. is same as the sum of its first 28 terms. Find the sum of its 48 terms.
Solution:
In an A.P.
Sum of first 20 terms = Sum of first 28 terms
Let a be the first term and d be the common difference, therefore
\(\frac{20}{2}[2 a-(20-1) d]=\frac{28}{2}[2 a-(28-1) d]\)
10(2a – 19d) = 14(2a – 27d)
20a – 190d= 28a- 318d
378d – 190d = 28a – 20a
⇒ 8a= 188d
2a = 47d
Now, sum of 48 terms
\(\frac{48}{2}[2 a-(48-1) d]\)
= 24[2a – 47 d]
= 24[47d – 41d] = 0
∴ Sum of first 48 terms = 0
Question 18.
If a, b, c are in A.P., show that : (b + c), (c + a) and (a + b) are also in A.P.
Sol.
a, b, c are in A.P.
∴ a – (a + b + c), b – (a + b + c), c – (a + b + c) are in A.P.
⇒ -(b + c), -(a + a), -(a + b) are in A.P.
⇒ (b + c), (c + a), (a + b) are in A.P.
Question 19.
If a, b, c are in GP.; a, x, b are in A.P. and b, y, c are also in A.P.
Prove that: \(\frac{1}{x}+\frac{1}{y}=\frac{2}{b}\).
Solution:
a, b, c are in G.P.
∴ B2 = ac
a, x, b are in A.P.
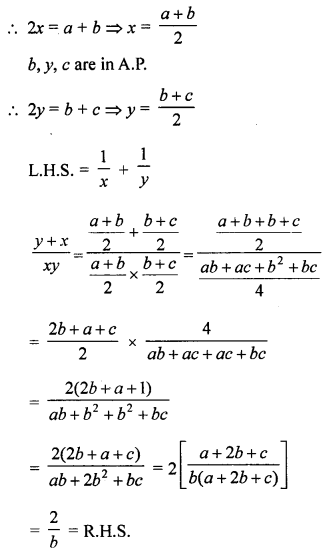
Question 20.
Evaluate: 9 + 99 + 999 + ………. upto n terms.
Solution:
9 + 99 + 999 + ……… n terms
= (10 – 1) + (100 – 1) + (1000 – 1) + …… n terms
= 10 + 100 + 1000 + ………. n terms -(1 + 1 + 1 + ……… n terms)
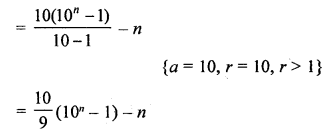
Question 21.
Find the point on the y-axis whose distance from the points (3, 2) and (-1, 1.5) are in the ratio 2:1.
Solution:
Let P he the point on the linesegment joining the two points A (3, 2) and B (-1, 1.5) and lies on y-axis.
Let co-ordinates of P be (0, y)
∵ P divides the line segment AB in the ratio of 2 : 1
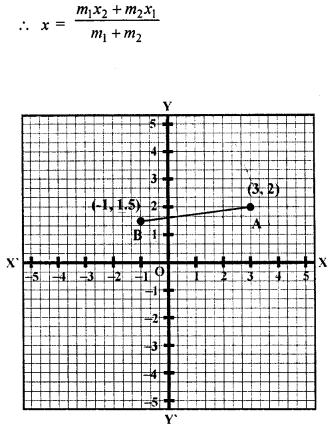
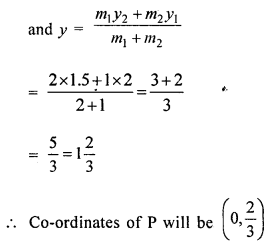
Question 22.
In what ratio does the point P (a, 2) divide the line segment joining the points A (5, -3) and B (-9, 4) ? Also, find the value of ‘a’.
Solution:
Let the point P (a, 2) divides the line segment joining the points A (5, -3) and B (-9, 4) in the ratio m1 : m2
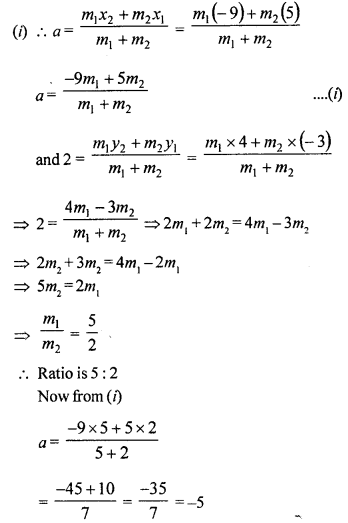
Hence Ratio is 5 : 2
and a = -5
Question 23.
A straight line makes on the co-ordinate axes positive interceps whose sum is 5. If the line passes through the point P(-3, 4), find its equation.
Solution:
Let a, b he the positive intercepts made by the line which passes through P(-3, 4) and a + b = 5
Now equation of the line
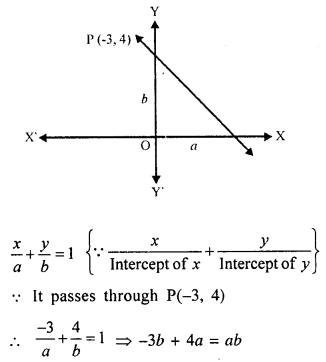
∵ a + b = 5 ⇒ b = 5 – a
∴ -3 (5 – a) + 4a = a (5 – a)
⇒ -15 + 3a + 4a = 5a – a2
⇒ -15 + 7a = 5a – a2
⇒ a2 + 7a – 5a – 15 = 0
⇒ a2 + 2a – 15 = 0
⇒ a2 + 5a – 3a – 15 = 0
⇒ a(a + 5) – 3(a + 5) = 0
⇒ (a + 5) (a – 3) = 0
Either a + 5 = 0 then a = -5, which is not possible as a and b are positive or a – 3 = 0, then a = 3
∴ b = 5 – a = 5- 3 = 2
∴ Equation of the line will be
\(\frac{x}{a}+\frac{y}{b}=1 \Rightarrow \frac{x}{3}+\frac{y}{2}=1\)
or 2x + 3y = 6
Question 24.
The line 3x – 4y + 12 = 0 meets x-axis at points A and y-axis at point B, Find :
(i) the co-ordinates of A and B.
(ii) equation of perpendicular bisector of line segment AB
Solution:
Equation of line is 3x – 4y + 12 = 0, which intersects x-axis at A and y-axis at B
Let co-ordinates of A be (x, 0) and of B be (0, y)
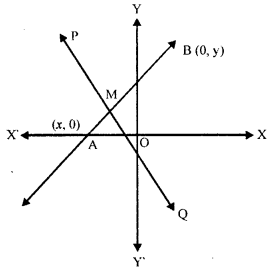
∵ These lie on the line
∴ 3x – 4 × 0 + 12 = 0
⇒ 3x + 12 = 0 ⇒ 3x = -12
\(x=\frac{-12}{3}=-4\)
∴ Co-ordinates of A will be (-4, 0)
Again 3 × 0 – 4y +12 = 0
0 – 4y = -12
⇒ – 4y = -12
⇒ \(y=\frac{-12}{-4}=3\)
∴ Co-ordinates of B will be (0, 3)
(ii) Let PQ be the perpendicular bisector of line segment AB which intersects it at M
∴ Co-ordinates of M will be \(\left(\frac{-4+0}{2}, \frac{0+3}{2}\right)\) or \(\left(-2, \frac{3}{2}\right)\)
Slope of line AB = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{3-0}{0-(-4)}=\frac{3}{4}\)

Question 25.
In a triangle PQR, L and M are two points on the base QR such that ∠LPQ = ∠QRP and ∠RPM = ∠RQB Prove that :
(i) ∆ PQL ~ ∆ RPM
(ii) QL × RM = PL × PM
(iii) PQ2 = QR × QL
Solution—
Given : In ∆ PQR, L and M are two points on base QR such that ∠LPQ = ∠QRP and ∠RPM = ∠RQP
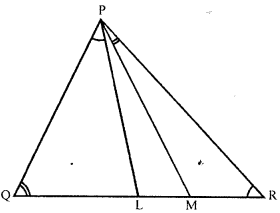
To prove :
(i) ∆PQL ~ ∆ RPM
(ii) QL × RM = PL x PM
(iii) PQ2 = QR × QL

Question 26.
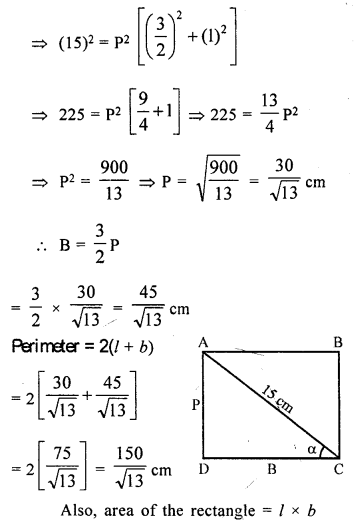
In a rectahgle ABCD, its diagonal AC = 15 cm and ∠ACD = α. If cot α = \(\frac{3}{2}\), find the perimeter and the area of the rectangle.
Solution:

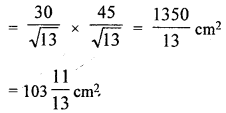
Question 27.
In the given figure : AB is a diameter of the circle. Chords AC and AD produced to meet the tangent to the circle at a point B in points P and Q respectively. Prove that :
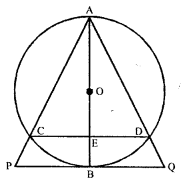
AB2 = AC × AP
(ii) C, B, Q and P are concyclic.
Solution:
Given : AB is a diameter of a circle – chords ‘ AC and AD produced meet the tangent to the circle at B in points P and Q, respectively.
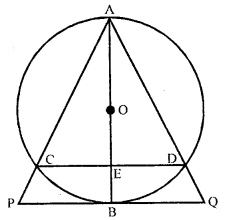
To prove :
(i) AB2 = AC × AP
(ii) C,D,Q and P are concyclic.
Proof : (i) ∵ AB is diameter and PQ is tangent.
∴ AB ⊥ PQ.
Now, in right ∆ APB,
PB2 = AP2 – AB2 …..(i)
∵ PB is tangent and PCA is secant
∴ PB2 = PA.PC = AP.PC …..(ii)
From (i) and (ii),
AP.PC – AP2 – AB2
⇒ AB2 = AP – AP . PC
= AP (AP – PC)
= AP × AC –
(iii) ∵ AOB is diameter and PQ is tangent and CD is chord,
∴ AOB ⊥ PQ + AE ⊥ CD
∴ AP = AQ and AC = AD
∴ CD || PQ and ∠P = ∠Q, ∠ACE = vADE
But ∠P = ∠ACE and ∠Q = ∠ADE (Corresponding angles)
But ∠ACE + ∠ECP = 180° (Linear pair)
∴ ∠P + ∠ECP = 180°
⇒ ∠Q+ ∠ECP = 180°
But there are the opposite angles of quadrilateral CDQP.
∴ CDQP is a cyclic quadrilateral Hence C,D,Q,P are concyclic.
Hence proved.
Question 28.
Use ruler and compasses for this question.
(i) Construct an isosceles triangle ABC in which AB = AC = 7.5 cm and BC = 6 cm
(ii) Draw AD, the perpendicular from vertex A to side BC.
(iii) Draw a circle with centre A and radius 2.8 cm, cutting AD at E.
(iv) Construct another circle to circumscribe the triangle BCE.
Solution:
Steps of construction :
(i) Draw a line segment BC = 6cm
(ii) with centres B and C, radius 75 cm draw to arcs intersecting each other at A
(iii) Join AB and AC
(iv) Draw AD perpendicular bisector of BC
(v) with centre A and radius 2.8 cm draw a circle which intersects AD at E
(vi) Join EB and draw its perpendicular bisector intersecting AD at O.
(vii) With centre O and radius OE, draw a circle which passes through B and C and touches the first circle at E externally. This is the required circle.
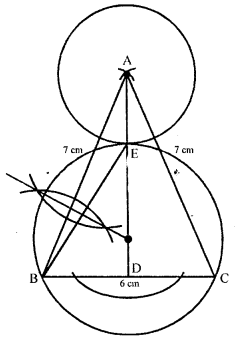
Question 29.
In triangle ABC, ∠BAC = 90°, AB = 6 cm and BC = 10 cm. A circle is drawn inside the triangle which touches all the sides of the triangle (i.e., an incircle of A ABC is drawn). Find the area of the triangle excluding the circle.
Solution:
In ∆ ABC, ∠BAC = 90°,
AB = 6cm, BC = 10cm
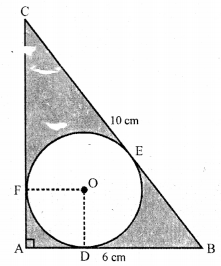
∴ AC2 = BC2 – AB2 (By Pythagoras Theorem)
= 102 – 62
= 100 – 36 = 64 = 82
∴ AC = 8 cm.
∴ Area ∆ ABC = \(\frac{1}{2}\) × AB × AC
= \(\frac{1}{2}\) × 6 × 8 = 24 cm2
A circle is drawn which touches the sides of the ∆ ABC at D, E and F respectively Join OD, OF which are the radius of the circle.

Question 30.
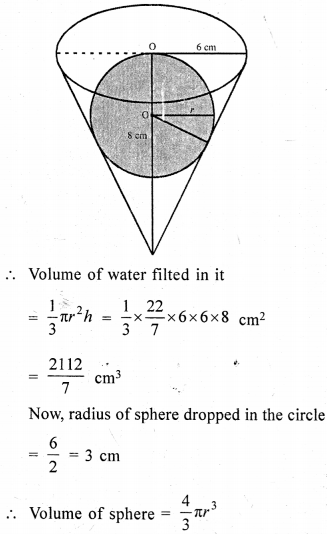
A conical vessel of radius 6 cm and height 8 cm is completely filled with water. A shpere is lowered into the water and its size is such that when it touches the sides it is just immersed. What fraction of water overflows?
Solution:
Radius of conical vessel = 6 cm
and height = 8cm
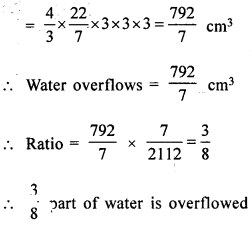
Question 31.
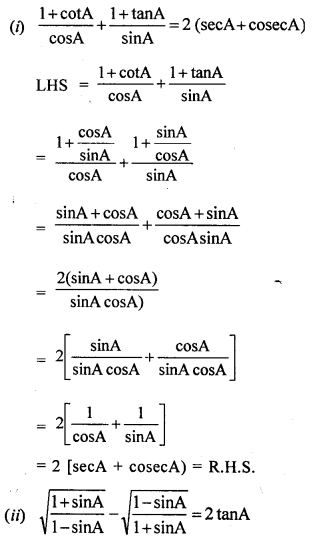
Prove that:
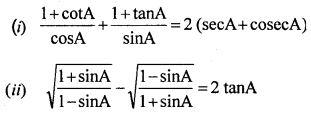
Solution:

Question 32.
Solve x ϵ W, o° ≤ x ≤ 90°.
(i) 3 tan2 2x = 1
(ii) tan2 x = 3 (secx – 1)
Solution:
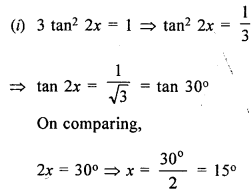
tan2 x = 3 (sec x – 1)
⇒ sec2 x – 1 = 3 (sec x – 1)
⇒ (sec x – 1) (sec x + 1) -3 (sec x – 1) = 0
⇒ (sec x – 1) [sec x + 1 – 3] = 0
⇒ (sec x – 1) (sec x – 2) = 0
Either sec x – 1 = 0, then sec x = 1 = sec 0°
Comparing, x = 0°
or sec x – 2 = 0, then sec x = 2 = sec 60°
∴ x = 60°
∴ x = 0°, 60°
Question 33.
The angle of elevation of the top of a tower as observed from a point on the ground is ‘a’ and on moving ‘a’ metre towards the tower, the angle of elevation is ‘P’.
Prove that the height of the tower is : \(\frac{\alpha \tan \alpha \tan \beta}{\tan \beta-\tan \alpha}\).
Solution:
Let AB be tower and two points C and D are two points making angles of elevation with top Of tower A area and P respectively and CD = a,
Let AB = h and BD = x
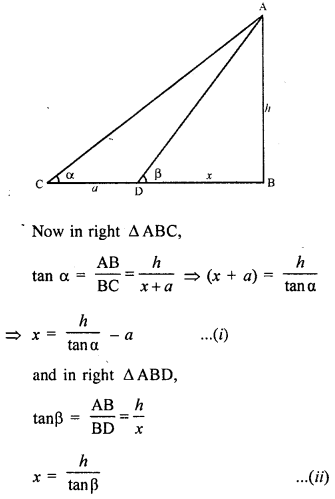
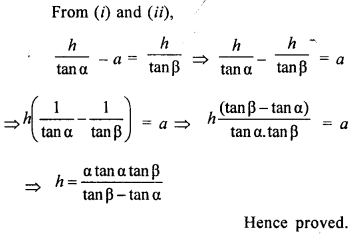
Question 34.
The mean of the following frequency distribution is 50, but the frequencies f1 and f2 in class 20 – 40 and 60 – 80 respectively are not known. Find these frequencies.
| Class | 0-20 | 2040 | 40-60 | 60-80 | 80-100 |
| Frequencies | 17 | f1 | 32 | f2 | 19 |
Given that the sum of frequencies is 120.
Solution:
Means = 50
| Class | Frequencies (f) | Class mark x | f × x |
| 0-20 | 17 | 10 | 170 |
| 2040 | f1 | 30 | 30f1 |
| 40-60 | 32 | 50 | 1600 |
| 60-80 | f2 | 70 | 70f2 |
| 80-100 | 19 | 90 | 1710 |
| Total | 68+ f1 + f2 = 120 | 3480 + 30f1 + 70f2 |
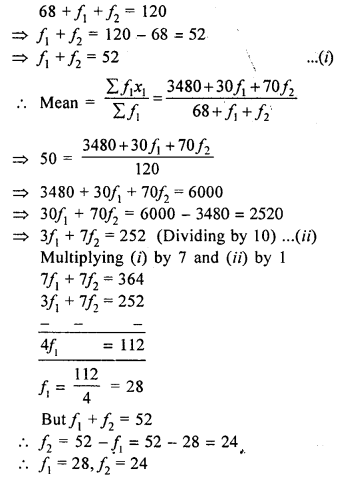
Question 35.
A card is drawn at random from a well- shuffled deck of 52 playing cards. Find the probability that it is :
(i) an ace
(ii) a jack of hearts
(iii) a three of clubs or a six of diamonds
(iv) a heart
(v) any suit except heart
(vi) a ten or a spade
(vii) neither a four nor a club
(viii) a picture card
(ix) a spade or a picture card.
Solution:
Number of possible outcome = 52
(i) Number of ace in the deck = 4



