Rationalizing Denominators with Radicals

Situation 1 – Monomial Denominator
When the denominator is a monomial (one term), multiply both the numerator and the denominator by whatever makes the denominator an expression that can be
simplified so that it no longer contains a radical.
* Sometimes the value being multiplied happens to be exactly the same as the denominator,
as in this first example (Example 1):
Example 1: Simplify 2/√7
Solution :
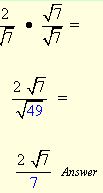
Explanation: Multiplying the top and bottom by √7 will create the smallest perfect square under the square root in the denominator.
Replacing √49 by 7 rationalizes the denominator.
* Sometimes it is necessary to multiply by whatever makes the denominator a perfect square or perfect cube or any other power that can be simplified, as seen in the next examples (Examples 2 and 3).
Example 2: Simplify 5/√8
Solution :
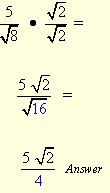
Explanation : Multiply by a value that will create the smallest perfect square under the radical. This will prevent the need for additional simplifications.
Choosing to multiply by √2 (and not √8 ) will create the smallest perfect square under the radical in the denominator.
Example 3: Simplify 4/3√9
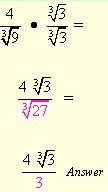
Multiplying by 3 √3 will create the smallest perfect cube under the radical.
Replacing by 3 √27, rationalizes the denominator.
Situation 2 – More than One Term in Denominator
When there is more than one term in the denominator, the process is a little tricky. You will need to multiply the numerator and denominator by the the denominator’s conjugate. The conjugate is the same expression as the denominator but with the opposite sign in the middle, separating the terms.
Example 4:
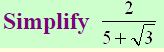
Solution :

Explanation : Multiply top and bottom by the conjugate of the denominator,5- √3 . Notice that you are multiplying by 1, which does not change the original expression.
When multiplying the denominators in this problem, distribute or use FOIL.
Notice what is happening to the middle terms when you multiply the denominators. The middle terms will drop out. Also, the last term has created a perfect square under the square root.
If possible, always reduce your final answer. In this problem, a factor of 2 can be removed from the top and bottom.
Did you notice that in this problem, we never distributed the 2 in the numerator? It is often best to work with the denominator first, and then see what else needs to be done.
Example 5:
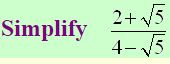
Solution
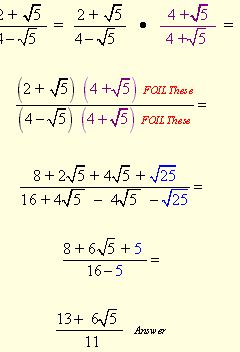
Explanation : Multiply top and bottom by the conjugate of the denominator, 4+√3 In this problem, we will need to multiply out both the numerator and the denominator. Again you can use the distributive method or FOIL.
Notice that while the middle terms are going to drop out on the bottom, they are not going to drop out on the top. This is OK. We just want the radical gone from the bottom.
Combine terms. The answer has a radical in the numerator. This is OK. The bottom does NOT have a radical, which was our goal.
Situation 3 – Working with a Reciprocal
When working with the reciprocal of an expression containing a radical, it may be necessary to rationalize the denominator.
Example 6: Write the reciprocal of 4 – √3
Solution :
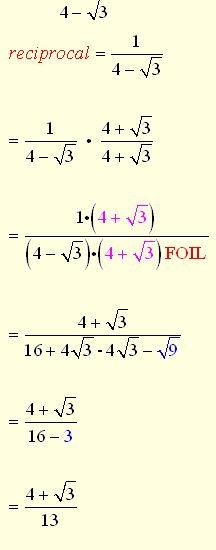
Explanation : Here is our starting expression.
The reciprocal is created by inverting the numerator and denominator of the starting expression.
Since we now have a radical in the denominator, we must rationalize this denominator. Multiply top and bottom by the conjugate of the denominator 4 – √3
Multiply the denominators in this problem, by using the distribute method or FOIL.
Again, we see the middle terms dropping out.
Simplify and combine.
Remember, that a radical 4 – √3 in the top is OK.