Kerala Plus Two Physics Previous Year Question Paper March 2018 with Answers
| Board | SCERT |
| Class | Plus Two |
| Subject | Physics |
| Category | Plus Two Previous Year Question Papers |
Time: 2 Hours
Cool off time : 15 Minutes
Maximum : 60 Score
General Instructions to candidates:
- There is a ‘cool off time’ of 15 minutes in addition to the writing time of 2 hrs.
- You are not allowed to write your answers nor to discuss anything with others during the ‘cool off time’.
- Use the ‘cool off time’ to get familiar with the questions and to plan your answers.
- Read questions carefully before you answering.
- All questions are compulsory and only internal choice is allowed.
- When you select a question, all the sub-questions must be answered from the same question itself.
- Calculations, figures and graphs should be shown in the answer sheet itself.
- Malayalam version of the questions is also provided.
- Give equations wherever necessary.
- Electronic devices except non programmable calculators are not allowed in the Examination Hall.
The given value of constants can be used wherever necessary.
Velocity or light in vacuum, c = 3 × 108 m/s
Plank’s constant, h = 6.64 × 10-34 Js
Charge of electron, e = 1.6 × 10-19C
Mass of the electron, m = 9.1 × 10-31 kg
Avogadro number = 6.025 × 1023 atom/mol
ε0 = 8.854 × 10-12 C2 N-1 m-2
μ0 = 4π × 10-7 Tm/A
Questions 1 and 2 carry 1 Score each. Answer both. (2 × 1 = 2)
Question 1.
How will you represent a resistance of 3700 Ω ± 5% using colour code?
Answer:
Orange, Violet, Red and Gold.
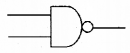
Question 2.
Draw the symbol of NAND gate.
Answer:
Answer any six questions from question number 3 to 10. Each question carries 2 Scores. (Scores: 6 × 2 = 12)
Question 3.
Two equal and opposite charges placed in air as shown in figure:

a) Redraw the figure and show the direction of dipole moment (P), direction of resultant electric field (E) at P.
b) Write an equation to find out the electric field at P.
Answer:
a)
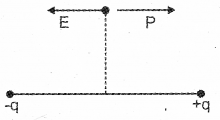
b) \(\overline{\mathrm{E}}=\frac{1}{4 \pi \varepsilon_{0}} \frac{\overline{\mathrm{P}}}{\mathrm{r}^{3}}\)
Question 4.
Calculate the electrical capacitance of earth. The radius of earth is 6400 km.
Answer:
Capacitance of earth C = \(4 \pi \varepsilon_{0} \mathrm{R}\)
C = \(4 \pi \varepsilon_{0}\) × 6400 × 103
= 710.8 µF
Question 5.
What do you mean by drift velocity? Write the relation between drift velocity and electric current.
Answer:
The average velocity acquired by an electron under the applied electric field is called drift velocity.
I = neAVd
Question 6.
A galvanometer is connected as shown in the figure:

a) This combination can be used as ………..
(voltmeter/rheostat/ammeter)
b) Derive an expession to find the value of resistance S.
Answer:
a) Ammeter
b)
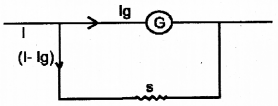
Let G be the resistance of the galvanometer, giving full deflection for a current Ig.
To convert it into an ammeter, a suitable shunt resistance ‘S’ is connected in parallel. In this arrangement Ig current flows through Galvanometer and remaining (I – Ig) current flows through shunt resistance.
Since G and S are parallel
P.d Across G = p.d across S
Ig × G = (I – Ig)s
Question 7.
An unpolarised light incident on a medium as shown in figure.
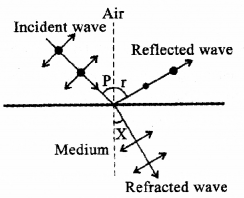
Show that the direction of reflected and refracted waves are mutually perpendicular.
Answer:
According to Brewster’s law
n = tan p = \(\frac{\sin p}{\cos p}\) ………(1)
According to Snell’s law
n = \(\frac{\sin p}{\sin x}\) …….(2)
Comparing (1) and (2), we get
\(\frac{\sin p}{\sin x}=\frac{\sin p}{\sin x}\)
sin x = cos p = sin(90 – p)
x = 90 – p, but p = r
x = 90 – r
x + r =90°
If x + r is 90°, angle between reflected and refracted ray will be 90°.
Question 8.
How many electrons, protons and neutrons are there in 16g of 8O16?
Answer:
Number of atoms in 16g of 8O16 = 6.023 × 1023
Number of protons = 8 × 6.023 × 1023
Numberof neutrons = 8 × 6.023 × 1023
Question 9.
The given block diagram shows general form of a communication system.

a) Identify the blocks X and Y.
b) What is the difference between attenuation and amplification?
Answer:
a) X – transmitter
Y – Receiver
b) Attenuation: The loss of strength of a signal while propagating through a medium is known as attenuation.
Amplification: It is the process of increasing the amplitude of a signal.
Question 10.
What is the population covered by the transmission, if the average population density around the tower is 1200 km-2? The antenna height is 160 m.
Answer:
Distance travelled by the wave d = \(\sqrt{2 R h}\)
Area = πd2
= π(\(\sqrt{2 R h}\))2
= π2Rh
= 3.14 × 2 × 6400 × 0.160 Km2
Population covered = Area × population density
= 3.14 × 2 × 6400 × 0.16 × 1200
= 7.72 × 106
Answer any five questions from question number 11 to 16. Each question carries 3 Scores. (Scores: 5 × 3 = 15)
Question 11.
Two spheres encloses charges as shown in figure:
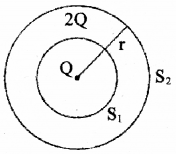
a) Derive and expression for electric field intensity at any point on the surface S2.
b) What is the ratio of electric flux through S1 and S2?
Answer:
a) According to Guess law

b) Flux a charge
for first sphere Φ1 α Q
for second sphere Φ2 α 3Q
∴ \(\frac{\phi_{1}}{\phi_{2}}=\frac{Q}{3 Q}=\frac{1}{3}\)
= 1 : 3
Question 12.
The electric field lines of a positive charge is as shown in figure:
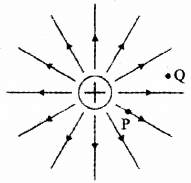
a) Give the sign of potential difference Vp – Vq.
b) Give the sign of work done by the field in moving a small positive charge from ‘Q’ to ‘P’.
c) What is the shape of equipotential surface near the charge?
Answer:
a) positive.
b) negative.
c) spherical.
Question 13.
a) Name the part of electromagnetic spectrum:
i) used in radar systems.
ii) produced by bombarding a metal target by a high speed electrons.
b) Electromagnetic waves are produced by ………..
(charges at rest/charges in uniform motion/ charges in accelerated motion)
c) Why only microwaves are used in microwave ovens?
Answer:
a) i) Micro waves
ii) X – rays
b) Charges in accelerated motion.
c) The frequency of micro waves matches with the rotational frequency of water molecule.
Question 14.
Two thin convex lenses of focal length f1 and f2 are placed in contact:
a) If the object is at principal axis, draw ray diagram of the image formation by this combination of lenses.
b) Obtain a general expression for effective focal length of the combination in terms of f1 and f2.
Answer:
a)
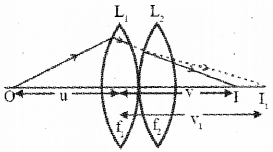
b) Consider two thin convex lenses of focal lengths f1 and f2 kept in contact. Let O be an object kept at a distance ‘u’ from the first lens L1, I1 is the image formed by the first lens at a distance v1.
Then from the lens formula, we can write,
\(\frac{1}{f_{1}}=\frac{1}{v_{1}}-\frac{1}{u}\) ……..(1)
This image will act as the virtual object for the second lens and the final image is formed at I (at a distance v). Then
\(\frac{1}{f_{2}}=\frac{1}{v}-\frac{1}{v_{1}}\) ……..(2)
Adding eq (1) and eq (2)
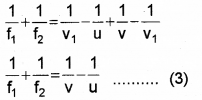
If the two lenses are replaced by a single lens of focal length ‘F’ the image is formed at ‘v’. Then we can write,
\(\frac{1}{F}=\frac{1}{v}-\frac{1}{u}\) …….(4)
from eq(3) and (4),
\(\frac{1}{F}=\frac{1}{f_{1}}+\frac{1}{f_{2}}\) …….(3)
Question 15.
A plane wave-front AB incident on a surface XY and undergoes refraction as shown in figure:
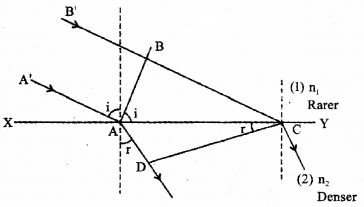
a) Prove Snell’s law of refraction by using this figure.
b) What is the change in speed of propagation and frequency of the refracted wave?
Answer:
a) AB is the incident wavefront and c1 is the velocity of the wavefront in the first medium. CD is the refracted wavefront and c2 is the velocity of the wavefront in the second medium. AC is a plane separating the two media.
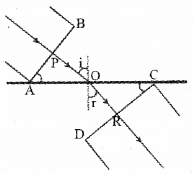
The time taken for the ray to travel from P to R is
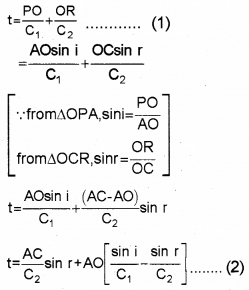
O is an arbitrary point. Hence AO is a variable.
But the time to travel a wavefront from AB to CD is constant. In order to satisfy this condition, the term containing AO in eq (2) should be zero.
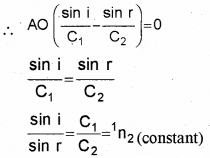
where 1n2 is the refractive index of the second medium w.r.t. the first. This is the law of refraction.
b) Speed decreses
frequency remains same.
Question 16.
a) State radioactive decay law.
b) Prove the relation N(t) = N0e-λt.
Answer:
a) The number of nuclei undergoing decay per unit time is proportional to number of nuclei in the sample at that time.
b) According to Law of Radioactive decay,
\(\frac{\mathrm{d} \mathrm{N}}{\mathrm{d} \mathrm{t}}\) = -λN
\(\frac{\mathrm{d} \mathrm{N}}{\mathrm{d} \mathrm{t}}\) = -λdt
Integrating
In N = -λt + C …….. (1)
C is the constant of integration. To get value of C, let us assume that initially (t = 0) the number of nuclei be N0.
∴ C = In N0
Substituting for C in equation (1) we get,
In N – In N0 = -λt
In \(\frac{\mathrm{N}}{\mathrm{N}_{0}}\) = -λt
\(\frac{\mathrm{N}}{\mathrm{N}_{0}}\) e-λt
N = N0e-λt
Answer any four questions from question number 17 to 21. Each question carries 4 Scores. (4 × 4 = 16)
Question 17.
Two charged partjeles q1 and q2 are moving through a uniform magnetic field (B) as shown in figure:
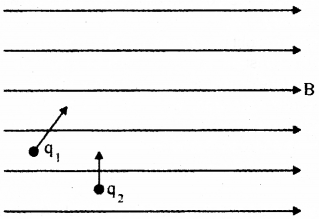
a) What is the shape of path of q1 and q2.
b) Derive an expression for cyclotron frequency with the help of a neat diagram.
Answer:
a) q1 charges undergoes helical motion and q2 moves in a circular path.
b)
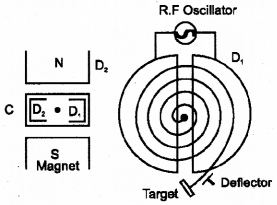
Let ‘v’ be the velocity of ion, q the charge of the ion and B the magnetic flux density. If the ion moves along a semicircular path of radius ‘r’, then we can write

Question 18.
The B-H curve of a ferromagnetic material is as shown in figure:

a) What do you mean by ferromagnetic material? Write any two properties of it.
b) Identify the value of retentivity and coercivity from the figure.
c) A solenoid has a core of a material with relative permeability 400. The windings of the solenoid are insulated from the core and carry a current of 2A. If the number of turns is 1000 per metre, calculate magnetic intensity (H) and magnetic field (B).
Answer:
a) Ferromagnetic substances are those which gets strongly magnetized in an external magnetic field.
Properties: High susceptibility and permeability.
b) Ob represents retentivity and Oc coercivity.
c) H = nI
= 1000 × 2
= 2 × 103 A/m
B = µsµrH
= µ0 × 400 × 2 × 103
B = IT
Question 19.
a) Derive an expression for self inductance of a solenoid.
b) What do you mean by eddy current? Write any two applications of it.
Answer:
a) Consider a solenoid (air core) of length/.number of turns N and area cross section A. let ‘n’ be the no. of turns per unit length (n = N/I)
The magnetic flux linked with the solenoid,
Φ = BAN
Φ = μ0nIAN (since B = μ0 ni)
but Φ = LI
∴ LI = μ0nIAN
L = μ0nAN
If solenoid contains a core of relative permeability
μr
Then L = μ0μrnAN
b) when magnetic flux in a metal block changes, induced currents are produced. This current is called eddy current.
Applications:
- Magnetic beaking in trains
- Damping
- Induction furnace
Question 20.
The given graph shows the variation of KE with frequency of incident radiations for two surfaces A and B.
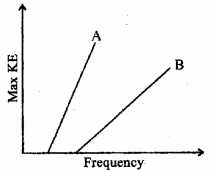
a) Which of the two metals has greater work function? For which of the metals will stopping potential be more for the same frequency of incident radiation?
b) The work function of caesium metal is 2.14 eV. When light of frequency 6 × 1014 Hz incident on the metal surface, what is the maximum KE of the photoelectrons and stopping potential?
Answer:
a) A
b) KE = hυ – Φ0
= 6.6 × 10-34 × 6 × 1014 – 2.14 × 1.6 × 10-19
= 0.551 × 10-19 J
= 0.345 eV
∴ Stopping potential = 0.345 V
Question 21.
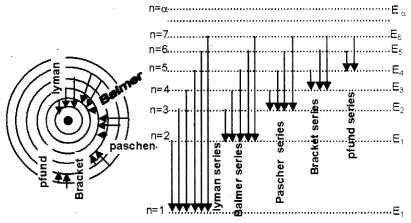
a) Name different series of lines observed in hydrogen spectrum.
b) Draw energy level diagram of hydrogen atom.
Answer:
a) Laymen, Balmer, Paschen, Bracket, Pfund
b)
Answer any three questions from question number 22 to 25. Each question carries 5 Scores. (Scores: 3 × 5 = 15)
Question 22.
The circuit diagram of a potentiometer for determining the emf ‘E’ of a cell of negligible internal resistance is as shown in figure.
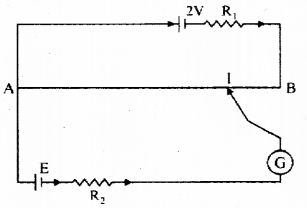
a) State the principle of working of a potentiometer.
b) How the balancing length AJ changes when the value of R1 decreases?
c) Derive an expression to find out internal resistance of a cell.
Answer:
a) Potential difference between two points of current carrying conductor is directly proportional to the length of the wire between two points.
b) Balancing length decreases.
c)
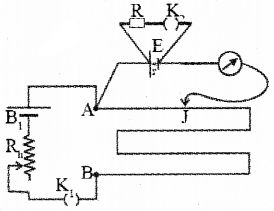
The key (K1) in the primary circuit is closed and the key is the secondary (K2) is open. Jockey is moved to get zero deflection in galvanometer. The balancing length l1 (from A) is found out.
Then we can write.
E1 ∝ l1 …….. (1)
Key K2 is put in the circuit, corresponding balancing length (l2) is found out. Let V be the applied voltage, then
V1 ∝ l1 ……..(2)
‘V’ is the voltage across resistance box.
Current through resistance box
i.e., voltage across resistance,

Question 23.
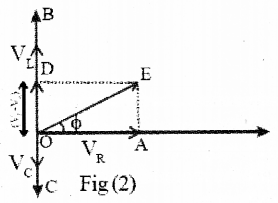
The phasor diagram of the alternating voltage across an unknown device X and current flowing through it are shown below.
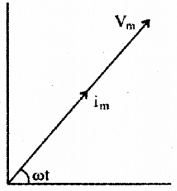
a) Identify the device X.
b) Draw the graphical variation of current and voltage with ωt through this device.
c) Draw the phasor diagram which shows the relation among VR, VL, VC and I in a series LCR circuit.
Answer:
a) Resistor
b)

c)
Question 24.
A ray of light passing through a prism. If the refracted ray QR is parallel to the base BC, as shown in figure.
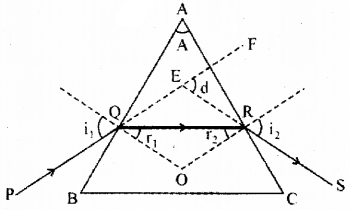
a) Derive an expression to find out deviation (d).
b) Draw a graph which shows the variation of ‘d’ with ‘i’.
c) Calculate the angle of minimum deviation if A = 60° and refractive index of the material of prism is 1.62.
Answer:
a)
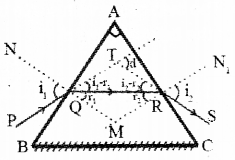
The angle between the emergent ray and incident ray is the deviation ‘d’.
In the quadrilateral AQMR,
∠Q + ∠R = 180°
[since N1M and NM are normal]
i.e., ∠A + ∠M = 180° …….(1)
In the Δ QMR,
∴ r1 + r2 + ∠M = 180° …….(2)
Comparing eq (1) and eq (2)
r1 + r2 = ∠A …….(3)
From the Δ QRT,
(i1 – r1) + (i2 – r2) = d
(i1 + i2) – (r1 + r2) = d
but, r1 + r2 = A
∴ (i1 + i2) – A = d

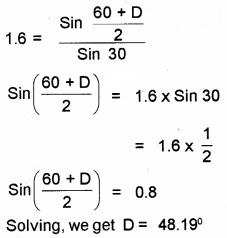
Question 25.
The symbol of a diode is shown in the figure:
![]()
a) The diode is a ………… (rectifier diode/photo diode/Zener diode)
b) Draw the VI characteristics of above diode.
c) A zener diode with VZ = 6.0 V is used for voltage regulation. The current through the load is to be 4.0 mA and that through the zener diode is 20 mA. If the unregulated input is 10.0 V, what is the value of series resistor R?
d) What is the fundamental frequency of the ripple in a full wave rectifier circuit operating from 50 Hz mains?
Answer:
a) Rectifier diode
b)
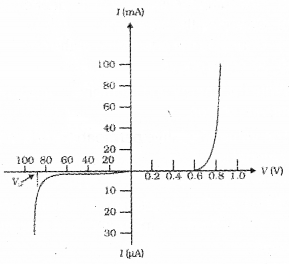
c) I = IZ + IL
= 20 × 10-3 + 4 × 10-3
I = 24 × 10-3 A
Resistance R = \(\frac{V}{1}=\frac{10-6}{24 \times 10^{-3}}\)
R = 166.67 Ω
d) 100 Hz