Kerala Plus Two Physics Previous Year Question Paper Say 2018 with Answers
| Board | SCERT |
| Class | Plus Two |
| Subject | Physics |
| Category | Plus Two Previous Year Question Papers |
Time: 2 Hours
Cool off time : 15 Minutes
Maximum : 60 Score
General Instructions to candidates:
- There is a ‘cool off time’ of 15 minutes in addition to the writing time of 2 hrs.
- You are not allowed to write your answers nor to discuss anything with others during the ‘cool off time’.
- Use the ‘cool off time’ to get familiar with the questions and to plan your answers.
- Read questions carefully before you answering.
- All questions are compulsory and only internal choice is allowed.
- When you select a question, all the sub-questions must be answered from the same question itself.
- Calculations, figures and graphs should be shown in the answer sheet itself.
- Malayalam version of the questions is also provided.
- Give equations wherever necessary.
- Electronic devices except non programmable calculators are not allowed in the Examination Hall.
You may use following Physical constants wherever necessary.
Mass of proton 1.66 × 10-27 kg
Mass of Electron 9.11 × 10-31 kg
Elementary charge, e = 1.6 × 10-19 C
Velocity of light in vacuum c = 3 × 108 m/s
Permittivity of free space ε0 = 8.85 × 10-12 F/m
Question Nos. 1 to 7 carry 1 score each. Answer 6 questions. (6 × 1 = 6)
Question 1.
Write the physical quantities having the following SI unit.
i) cm
ii) Ωm
Answer:
i) Electric dipole moment
ii) Electrical resistivity
Question 2.
A uniform wire of resistance 40Ω is cut into four equal parts and they are connected in parallel. The effective resistance of the combination is
i) 40Ω
ii) 10Ω
iii) 2.5Ω
iv) 4Ω
Answer:
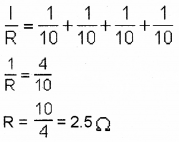
Question 3.
A particle of charge q is moving through a uniform magnetic field of intensity B with a velocity v. Write an expression for the force acting on the particle in vector form.
Answer:
\(\overrightarrow{\mathrm{F}}=\mathrm{q}(\overrightarrow{\mathrm{v}} \times \overrightarrow{\mathrm{B}})\)
Question 4.
The minimum distance between the object and its real image for a concave mirror of focal length f is
i) f
ii) 2f
iii) 4f
iv) zero
Answer:
iv) zero
Question 5.
Variation of photocurrent with collector plate potential for different intensities I1, I2, and I3 of incident radiation is shown below.
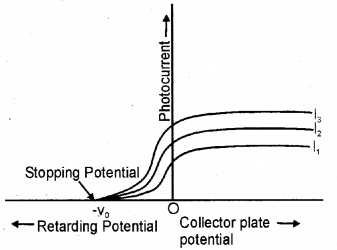
Arrange these intensities in the accending order.
Answer:
I3 > I2 > I1
Question 6.
An electron is revolving around the nucleus of a hydrogen atom in an orbit of radius nine times the radius of the first orbit. Angular momentum of the electron in this orbit is.
i) \(\frac{h}{2 \pi}\)
ii) \(\frac{9 h}{2 \pi}\)
iii) \(\frac{3 h}{\pi}\)
iv) \(\frac{3 h}{2 \pi}\)
Answer:
radius of the nucleus r = n2r0
In this case
∴ n2 = 9, n= 3
Angular momentum L = \(\frac{\mathrm{nh}}{2 \pi}\)
for third orbit L = \(\frac{3 h}{2 \pi}\)
Question 7.
The voltage – current characteristics of an optoelectronic junction device is shown below.
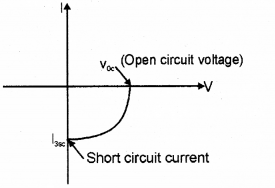
Identify the device.
Answer:
Solar cell
Question Nos. 8 – 15 carry 2 scores each. Answer any 7 questions. (7 × 2 = 14)
Question 8.
What is the radius of the circular path of an electron moving at a speed of 3 × 107 m/s in a magnetic field of 6 × 10-4 T perpendicular to it?
Answer:
radius r = \(\frac{m v}{q B}\)
v = 3 × 107 m/s, m = 9.1 × 10-31kg
B = 6 × 10-4, q = 1.6 × 10-19
r = \(\frac{9.1 \times 10^{-37} \times 3 \times 10^{7}}{1.6 \times 10^{-19} \times 6 \times 10^{-4}}\) = 0.285 m
Question 9.
a) “Parallel currents attract, and antiparallel currents repel”. State whether this statement is true or false.
b) Define the SI unit of current in terms of force between two current carrying conductors.
Answer:
a) True
b) Ampere is defined as that current which is main-tained in two straight parallel conductors of infi-nite length placed one meter apart in vacuum will produce between a force of 2 × 10-7 Newton per meter length.
Question 10.
A circular metallic loop and a current carrying conductor are placed as shown in figure.
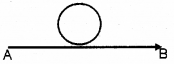
If the current through the conductor is increasing from A to B, find the direction of induced current the loop.
Answer:
Current flows in clockwise direction
Question 11.
a) The electric field vector of an electromagnetic wave is represented as Ex = Em Sin(kz – ωt). Write the equation for the magnetic field vector.
b) The ratio of intensity of magnetic field to intensity of electric field has the dimensions of
i) velocity
ii) acceleration
iii) reciprocal of velocity
iv) reciprocal of acceleration
Answer:
a) By = Bm Sin (Kz – ωt)
b) reciprocal of velocity
Question 12.
Write the equations for the following nuclear reactions:
a) β+decay of \({ }_{6}^{11} c\) to Boron (B)
b) β –decay of \({ }_{15}^{32} c\) to Sulphur (S)
Answer:
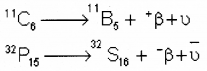
Question 13.
Write the truth table of the circuit shown below.
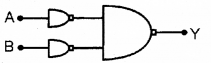
Answer:
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Question 14.
A TV transmitting antenna is 100 m tall. How much service area can it cover if the receiving antenna is at the ground level? Radius of earth is 6400 km.
Answer:
Hight of antenna, h = 100 m = 0.1 km
Radius of earth = 6400 km
Transmission range d = \(\sqrt{2 R h}\)
∴ Maximum area covered A = πd2
= π(\(\sqrt{2 R h}\))2
= 3.14 × 2 × 6400 × 0.1
= 4019 km2
Question 15.
Two magnetic dipoles P and Q are placed in a uniform magnetic field \(\vec{B}\) gas shown.

a) Both the dipoles do not experience any torque. Why?
b) Identify the dipole which is in most stable equilibrium.
Answer:
a) Dipole moment is parallel to magnetic field.
b) Dipole Q
Question Nos. 16 to 22 carry 3 scores each. Answer any 6 questions. (6 x 3 = 18)
Question 16.
The experimental setup for the comparison of two resistances is shown below.
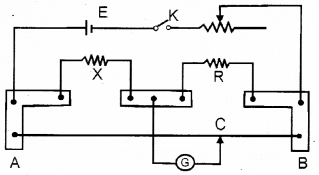
a) The working principle of the above device is
i) Ohm’s law
ii) Kirchhoffs second law
iii) Wheatstone’s principle
iv) Point Rule
b) In figure, Let X is the effective resistance of series combination of two 3Ω resistors and R is the effective of a parallel combination of two 3Ω resistors. The balance point is obtained at C. If the length AB is 100 cm. find the length AC of the wire.
Answer:
a) Wheatston’s principle
b) x = 6 Ω
R = 1.5 Ω
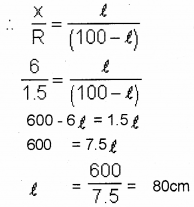
Question 17.
A magnetic needle has magnetic moment 6.7 × 10-7 Am2 and moment of inertia 7.5 × 10-6 kgm2. In a uniform magnetic field, it performs 10 complete oscillations in 6.70s. What is the magnitude of the magnetic field?
Answer:
magnetic moment m = 6.7 × 10-2 Am2
moment of inertria, I = 7.5 × 10-6 kgm2

Question 18.
With the help of a ray diagram, show the formation of image of a point object by refraction of light at a spherical surface separating two media of refractive indices n1 and n2. Using the diagram derive the relation
\(\frac{n_{2}}{v}-\frac{n_{1}}{u}=\frac{n_{2}-n_{1}}{R}\)
Answer:
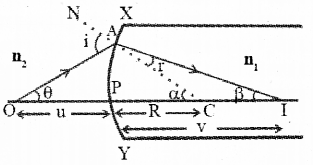
Consider a convex surface XY, which separates two media having refractive indices n1 and n2. Let C be the centre of curvature and P be the pole. Let an object is placed at ‘O’, at a distance ‘u’ from the pole. I is the real image of the object at a distance ‘V’ from the surface. OA is the incident ray at angle ‘i’ and AI is the refracted ray at an angle ‘r’. OP is the ray incident normally. So it passes without any deviation. From snell’s law,
sin i/sin r = \(\frac{\mathrm{n}_{2}}{\mathrm{n}_{1}}\)
If ‘i’ and ‘r’ are small, then sin i » i and sin r » r.
From the Δ OAC, exterior angle = sum of the interior opposite angles
i.e., i = α + θ ………(2)
Similarly, from Δ IAC,
α = r + β
r = α – β ………..(3)
Substituting the values of eq(2) and eq(3)in eqn.(1)
we get,
n1(α + θ) = n2(α – β)
n1α + n1θ = n2α – n2β
n1θ + n2β = n2α – n1α
n1θ + n2β = (n2 – n1)α ………..(4)
From OAP, we can write,

According to New Cartesian sign convection, we can write,
OP = -u, PI = +v and PC = R
Substituting these values, we get
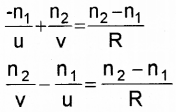
Question 19.
a) Draw a graph showing the variation of stopping potential with frequency of incident radiation. Mark the threshold frequency in the figure.
b) Using Einstein’s photoelectric equation, show that photoelectric emission is not possible if the frequency of incident radiation is less than the threshold frequency.
Answer:
a)
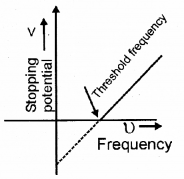
b) According to Einsten’s Equation
hν = hν0 + KE
if = ν < ν0, kinetic energy of electron becomes negative.
Question 20.
a) The energy levels of an atom are as shown in the figure.
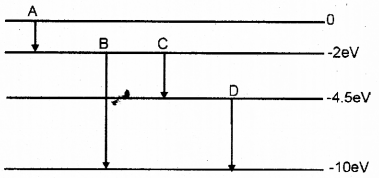
Which transition corresponds to emission of radiation of maximum wavelength?
b) Sketch the energy level diagram for hydrogen atom and mark the transitions corresponding to Balmer series.
Answer:
a) In between 0 to -2ev
b)

Question 21.
The decay rate of a radioactive ample is called its activity.
a) What is the SI unit of activity?
b) The half life of \({ }_{92}^{238} U\) against alpha decay is 1.5 × 10-17 s. Calculate the activity of a sample of \({ }_{92}^{238} U\) having 25 × 1020 atoms.
Answer:
a) becquerel
b) N = 25 × 1020, half life T1/2 = 1.5 × 1017s
activity, R = λN
R = \(\frac{0.693}{\mathrm{~T}_{1 / 2}} \times \mathrm{N}=\frac{0.693}{1.5 \times 10^{17}} \times 25 \times 10^{20}\)
R = 11550 Bq
Question 22.
a) Draw the circuit diagram where a zener diode is used as a direct voltage regulator.
b) In a zener regulated power supply a zener diode with zener voltage 4V is used for regulation. The load current is to be 4 m A and zener current is 20 mA. If the unregulated input is 10V, What should be the value of resistor that is to be connected in series with the diode?
Answer:
a)
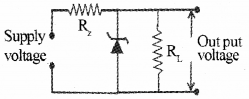
b) Zener voltage
V2 = 4V, IL = 4 × 10-3 A, I2= 20 × 10-3 A
Unregulated input = 10 v
Voltage across resister = 10 – 4 = 6v
Current through the resister = IL+ I2
= (4 + 20) mA
= 24 × 10-3 A
∴ resistance R = \(\frac{V}{I}\)
R = \(\frac{6}{24 \times 10^{-3}}\) = 250 Ω
Question Nos. 23 to 26 carry 4 scores each. Answer any 3 questions. (3 × 4 = 12)
Question 23.
Coulomb’s Law is a quantitative statement about the force between two point charges.
a) Write the mathematical expression of the above law.
b) Two ions carrying equal charges repel with a force of 1.48 × 10-8 N when they are separated by a distance of 5 × 10-10 m. How many electrons have been removed from each iron?
Answer:
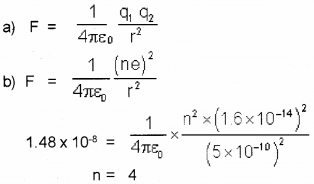
Question 24.
a) Potential energy of a system of charges is directly proportional to the product of charges and inversely to the distance between them.
a) Prove the above statement.
b) Two point charges 3 × 10-8 C and -2 × 10-8 C are separated by a distance of 15cm. At what point on the line joining the charges the potential is zero?
Answer:
a) Potential of a system is the work done to assemble the system,
∴ w = qV
= \(\mathrm{q}_{1} \times \frac{1}{4 \pi q_{0}} \frac{\mathrm{q}_{2}}{\mathrm{r}}\)
In the above equation it is dear that energy is di-rectly proportial to charges and inversely proportional to the distance between them.
b) q1 = 3 × 10-8
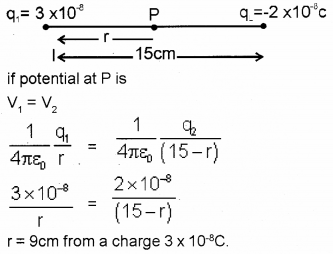
Question 25.
The circuit shown can be analysed using Kirchhoff’s rules.
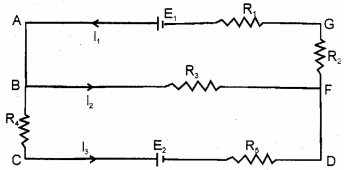
a) Apply Kirchhoffs first law to the point B.
b) State Kirchhoffs second law.
c) Apply Kirchhoffs second lawtothe mesh ABFGA.
Answer:
a) At the point B,
I1 = I2 = I3
b) In any closed circuit emf is eqaual to sum of potential drops.
c) -I2 R3 – I1 R2 – I1R1 + E1 = 0
Question 26.
Biot – Savart’s law relates current with the magnetic field produced by it.
a) Write the mathematical expression of the above law in vector form.
b) Using the law derive an expression for intensity of magnetic field at a point at distance x from the centre and on the axis of a circular current loop.
Answer:
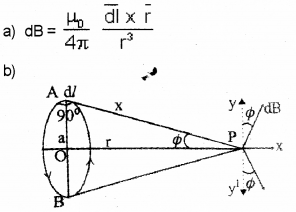
Consider a circular loop of radius ‘a’ and carrying current “I’. Let P be a point on the axis of the coil, at distance x from A and r from ‘O’. Consider a small length dl at A.
The magnetic field at ‘p’ due to this small element dI,
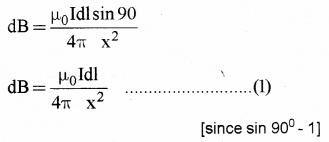
The dB can be resolved into dB cos Φ (along Py) and dBsinΦ (along Px).
Similarly consider a small element at B, which produces a magnetic field ‘dB’ at P. If we resolve this magnetic field we get.
dB sinΦ (along px) and dB cosΦ (along py1)
dBcosΦ components cancel each other, because they are in opposite direction. So only dB sinΦ components are found at P, so total filed at P is
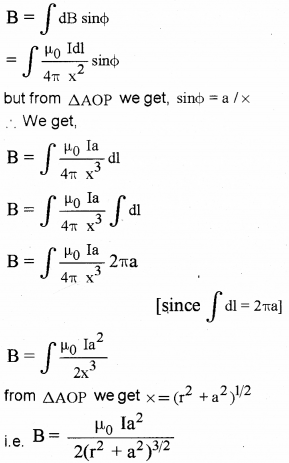
Let there be N turns in the loop then,
B = \(\frac{\mu_{0} \text { NIa }^{2}}{2\left(\mathrm{r}^{2}+\mathrm{a}^{2}\right)^{3 / 2}}\)
Question Nos. 27 to 29 carry 5 scores each. Answer any 2 questions. (2 × 5 = 10)
Question 27.
A series LCR circuit shows the phenomenon called resonance.
a) Write the condition for resonance and obtain an equation for resonant frequency.
b) Obtain the Q value of a series LCR circuit with L = 2.0 H, c = 32µ F and R = 10 Ω.
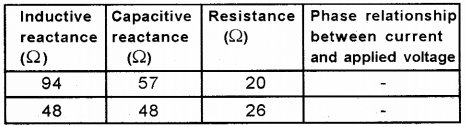
c) Complete the following table using the suitable words from the bracket for two series LCR circuits.
(Current and applied voltage are in the same phase, current leads the applied voltage, current lags the applied voltage)
Answer:
a) Condition for resonance XL = XC
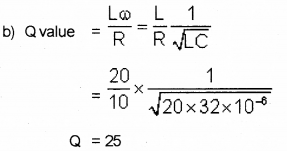
c) i) Cuurrent lags the applied voltage
ii) Current and applied voltage are in same phase.
Question 28.
Telscope is used to provide angular magnification of distant objects.
a) If f0 is the focal length of the objective and fe that of the eye piece, the length of the telescope tube is ………..
b) Draw the ray diagram of a refracting type telescope when it is in normal adjustment.
c) Write any two advantage of reflecting type telescope over refracting type telescopes.
Answer:
a) f0 + fe
b)
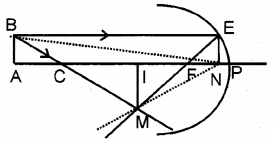
c) i) There is no chromastic aberration
ii) There is no spherical aberration
Question 29.
A wavefront is defined as a surface of constant phase.
a) The energy of the wave travels in a direction …….. to the wavefront.
b) Explain Huygen’s principle.
c) Using Huygen’s Principle, prove that angle of incidence is equal to angle of reflection.
Answer:
a) Perpendicular
b) 1) Every point in a wavefront acts as a source of secondary wavelets.
2) The secondary wavelets travel with the same velocity as the original value.
3) The envelope of all these secondary wavelets gives a new wavefront.
c)
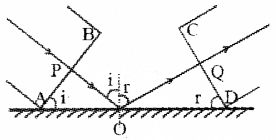
AB is the incident wavefront and CD is the reflected wavefront. T is the angle of incidence and Y is the angle of reflection. Let c, be the velocity of light in the medium. Let PO be the incident ray and OQ be the reflected ray.
The time taken for the ray to travel from P to Q is
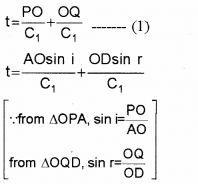
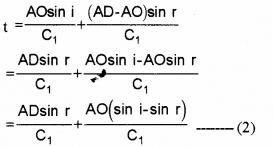
O is an arbitrary point. Hence AO is a variable. But the time to travel for a wave front from AB to CD is a constant. So eq.(2) should be independent of AO. i.e., the term containing AO in eq.(2) should be zero.
∴ \(\frac{A O}{C_{1}}\) (sin i – sin r) = 0
sin i – sin r = 0
sin i = sin r
i = r
This is the law of reflection.