Plus Two Physics Chapter Wise Previous Questions Chapter 4 Moving Charges and Magnetism

Plus Two Physics Chapter Wise Previous Questions Chapter 4 Moving Charges and Magnetism is part of Kerala Plus Two Physics Chapter Wise Previous Questions and Answers Kerala. Here we have given Plus Two Physics Chapter Wise Questions and Answers Chapter 4 Moving Charges and Magnetism.

Kerala Plus Two Physics Chapter Wise Previous Questions and Answers Chapter 4 Moving Charges and Magnetism

Question 1.
A particle of mass 1 x 10^-26 kg and charge 1.6 x 10^-19 C travelling with a velocity of 1.28 x 10⁶ m/s in the +X direction enters a region in which a uniform electric field § and a uniform magnetic field of induction B are present such that Ex = Ey = 0 and Ez = – 102.4 kV/m and Bx = Bz = 0, By = 8 x 10^-2 wb/m². The particle enters this region at the origin at time t = 0. (March – 2009)
a) Write the expression for the force experienced by the particle inside an electric field E
b) Find the force experienced by the particle in the electric field alone, in the above problem, (magnitude and direction)
c) Write the expression for the force experienced by the particle in a magnetic field.
d) Find the force experienced by the particle in the magnetic field alone, in the above problem, (magnitude and direction)
e) What is the resultant force on the particle in the above problem?
Answer:

e) The two forces acting on charge (force due to electric field and another force due to magnetic field) are of the same magnitude but opposite in direction.

Hence net force is zero.

Question 1.
Ampere’s circuital theorem is generally used to determine the magnetic field produced by a current-carrying element. (March – 2010)
a) State Ampere’s circuital theorem.
b) Obtain an expression for the magnetic field produced by an infinitely long straight conductor using Ampere’s circuital theorem.
c) A long straight conductor carries 35 ampere. Find the magnetic field produced due to this conductor at a point 20 cm away from the centre of the wire.
OR
A galvanometer is used to detect current in a circuit.
a) State the working principle of a moving coil galvanometer.
b) How will you convert a galvanometer into (i) an ammeter and (ii) a voltmeter?
c) A galvanometer coil has a resistance of 12 ohms. It shows a full-scale deflection for a current of 3 mA. How will you convert this into a voltmeter of range 0-18V?
Answer:
a) The line integral of the magnetic field around a closed loop is PO times, the current enclosed by the loop.
b) Long straight conductor: Consider a long straight conductor carrying T ampere current. To find the magnetic field at ‘P’, we construct a circle of radius r (passing through P).

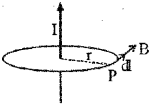
According to Ampere’s circuital law we can write

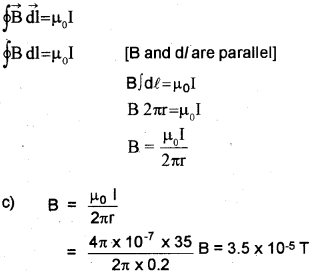
OR

a) A current-carrying loop when placed in a magnetic field experiences a torque.
b) A galvanometer can be converted in to ammeter by connecting a small resistance in parallel to it. A galvanometer can be converted into a voltameter by connected a high resistance in series with it.

c) l_g = 3 x 10^-3 A, G = 12Ω, V= 18 V
The resistance required to convert galvanometer in to voltmeter.

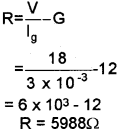
By connecting a resistance R = 5988 in series with a galvanometer, we can convert a galvanometer into a voltmeter.

Question 1.
A cyclotron is a device that accelerates charged particles for carrying out nuclear reactions. (Say – 2010)
a) With a suitable diagram, briefly explain its working principle and how charged particles get accelerated.
b) Find the energy of emergent protons (in MeV) coming from a cyclotron having dees of radius 2 metres, when a magnetic field of 0.8 T is applied. (Mass of proton = 1.67 x 10^-27 kg)
Answer:
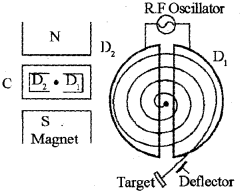
a) CYCLOTRON
Uses
It is a device used to accelerate particles to high energy.

Principles
Cyclotron is based on two facts

• An electric field can accelerate a charged particle.
• A perpendicular magnetic field gives the ion a circular path.

Working

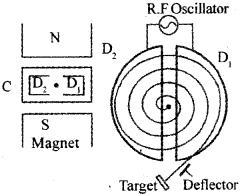
At certain instant, let D₁ be positive and D₂ be negative. Ion (+ve) will be accelerated towards D₂ and describes a semicircular path (inside it). When the particle reaches the gap, D₁, becomes negative and D₂ becomes positive. So ion is accelerated towards D₁ and undergoes a circular motion with larger radius. This process repeats again and again.

Thus ion comes near the edge of the dee with high K.E. This ion can be directed towards the target by a deflecting plate.

b) Maximum Kinetic energy

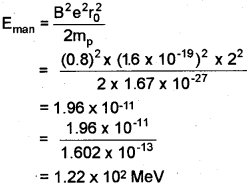
Question 1.
A moving charged particle of charge ‘q’ experiences a force both in electric field E and magnetic field B. (Say – 2011)
This force is called the ‘Lorentz force’.
a) Write down the relation for the Lorentz force.
b) A crossed electric and magnetic field is used as ………………..
c) ……………….. is a cyclic accelerator to accelerate charged particle or ions to high energies.
Answer:

b) Velocity selector
c) Cyclotron

Question 2
A current-carrying conductor placed in a magnetic field experiences a force. (Say – 2011)
a) Write down a relation for the force per unit length between two parallel conductors carrying current.
b) Use the above relation to define the unit of current. Given that m0 = 4p x 10^-7 H/m.
c) Calculate the force per unit length on a long straight wire carrying a current of 4A due to parallel wire carrying 6A current. The distance between the wires is 3 cm.
Answer:
a) \(F=\frac{\mu_{0} I_{1} l_{2}}{2 \pi r}\)
b) An ampere is defined as that constant current which if maintained in two straight parallel conductors of infinite lengths placed one meter apart in a vacuum will produœ between a force of 2 x 1O-7N per meter length.

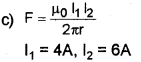
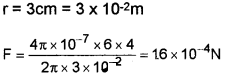
Question 1.
Oersted found that moving charges or currents produce a magnetic field in the surrounding space. (March – 2012)
a) An electric current is flowing due south along a power line. What is the direction of the magnetic field (i) above it and (ii) below it?
b) Draw a neat and labeled diagram of a cyclotron. State the underlying principle of its working.
c) A cyclotron’s oscillator frequency is 10 MH_z. What should be the operating magnetic field for accelerating protons? C = 1.6 x 10^-19 C, mass of proton np = 1.67 x 10^-27 kg.
Answer:
i) West
ii) East

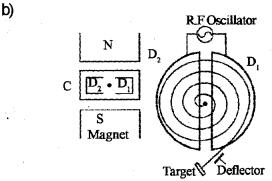
Cyclotron is based on two facts

• An electric field can accelerate a charged particle.
• A perpendicular magnetic field gives the ion a circular path.

c) Operating magnetic field

Question 1.
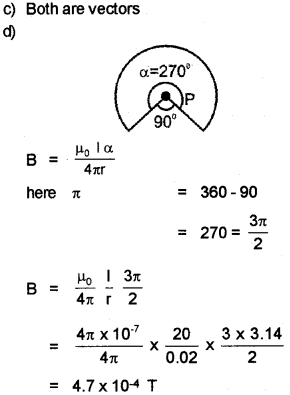
The direction of velocity of two charged particles in a magnetic field is shown below. (Say – 2012)

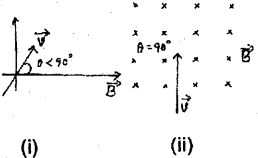
a) Sketch the path traced by the charged particle in each case.
b) “Magnetic force cannot do any work” Do you agree with this statement? Justify your answer.
c) According to Bohr atom model electrons are revolving in circular orbits around the nucleus. The movement of electrons can be regarded as a circular current flow. Then derive an expression for the magnetic dipole moment of an orbital electron.
Answer:

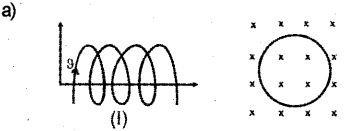
b) Yes. The direction of the magnetic force on a moving charge is always perpendicular to the direction of motion. Hence work done by the magnetic force on a moving charge is zero.

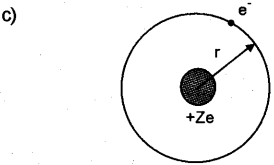
Consider an electron of charge -e. revolving around nucleus of charge +ze as shown in figure. If T Is the period of revolution

Question 1.
Force acting on a charged particle when it moves in a combined electric and magnetic field is known as Lorentz force. (March – 2013)
a) A charged particle is released from rest in a region of steady and uniform electric and magnetic fields; which are parallel to each other. What will be the nature of the path followed by the charged particle? Explain your answer.
b) A rectangular loop carrying a steady current is placed in a uniform magnetic field. Obtain the expression for the torque acting on the loop.
Answer:
a) Moves in straight line with acceleration. The directions magnetic field and electric field are in same direction. Electric field can produce acceleration on charged particle. Hence particle moves in the direction of electric field. The force due to magnetic field on the charged particles is zero. Hence effect of magnetic field is not considered in this case.

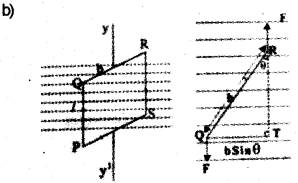
Considera rectangular coil PQRS of N turns, is suspended in a magnetic field, Let ‘I’ be the length (PQ) and ‘b’ be the bceadth (QR). When a current Iflows in the coil, each side produces a force. But the forces on PO and RS will produce a Torque.

Which can be written as

Question 1.
A Galvanometer is a device that can be used for measuring the value of current or voltage. (Say – 2013)
a) How will you convert a Galvanometer into an ammeter?
b) A Galvanometer with a coil resistance 12W shows full scale deflection fora current of 2.5mA. How will you convert it into an ammeter of range 0 – 7.5A?
Answer:
a) To convert a galvanometer in to ammeter a low resistance called shunt resistance is connected parallel to its terminals.

Question 2.
Particle accelerators are used to impart high energy to elementary particles. Cyclotron is such a device.
a) Explain what do you mean by magnetic Lorentz force.
b) A cyclotron oscillator frequency is 10 MHz. What should be the operating magnetic field for accel- erating protons?
[mass of proton mp = 1/67 x 10^-27 kg, e = 1.6 x 10^-19 C)
Answer:
a) The force acting on a moving charge in a magnetic field is called magnetic Lorentz force.
\(\bar{F}\) = q (\(\bar{u}\) x \(\bar{B}\))
Direction of force is perpendicular to both o and B. Hence the work done by magnetic force is zero.
b) Frequency u = 10 x 10⁶ Hz, mp = 1.6 x 10^-27 kg

Question 1.
The relation between magnetic field and current is given by Biot-Savart law. (March – 2014)
a) Illustrate Biot-Savart law with necessary figure.
b) Compare Biot-Savart law with Coloumb’s law for electrostatic field.
c) Give an expression for magnetic field on the axis of a circular current loop. (Expression only).
d) What is the value of B at the centre of the loop.
Answer:
a) The magnetic field at any point due to an element of the current-carrying conductor is

• Directty proportional to strength of current, I
• Directly proportional to length of element, dl
• Directly proportional to the sine of angle, 9 between the element and line joining midpoint of element to the point.
• Inversly proportional to square of the distance to the point from the element.
  

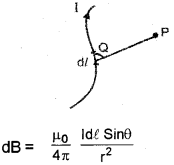
b) Similarities Coulomb’s law and Birt – Savart’s law

• The two laws are based on inverse square of distance & hence are long-range.
• Both electrostatic & magnetic fields obey the super-position principle.

Differences Coulomb’s law and Birt – Savart’s law
Coulomb’s law

• The source of electrostatic force is scalar (electric charge)
• The direction of electrostatic force is along dis-placement vector
• The electrostatic force is independent of angle.

Birt-Savart’s law

• The source of the magnetic field is vector. (Cur-rent element)
• The direction of magnetic field is the perpendicular-to plane containing displacement vector and current element.
• There is the dependence of angle in Biot-Savart law

Question 1.
Electric current can produce a magnetic field (Say – 2014)
a) Name the law which explains the relation between current and the magnetic field produced by the current.
b) Derive an equation showing the variation of this magnetic field with distance.
c) Can you suggest any similarity between the magnetic field produced by electric current and electric field produced by charges.

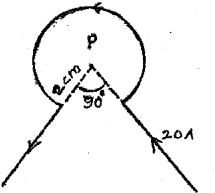
d) The wire shown in figure carries a current of 20A. Find the field at the point P.
Answer:
a) Biat Savart Law

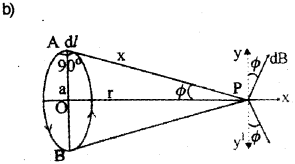
Consider a circular loop of radius ‘a’ and carrying current el’. Let P be a point on the axis of the coil, at distance x from A and r from ‘O’. Consider a small length dl at A.

The magnetic field at ‘p’ due to this small element dl,

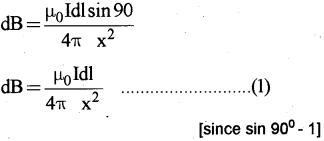
The dB can be resolved into dB cos4) (along Py) and dB sinΦ (along Px).
Similarly consider a small element at B, which produces a magnetic field dB’ at P. If we resolve this magnetic field we get.
dB sinΦ (along px) and dB cosΦ (along py1)
dB cosΦ components cancel each other, because they are in opposite direction. So only dB sinΦ components are found at P, so total filed at P is

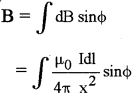
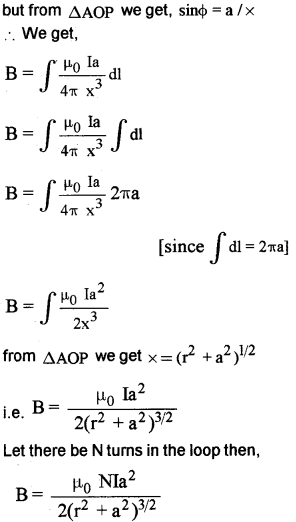
Question 2.
When a charged particle enters perpendicular to a magnetic field it experiences a force?
a) Nametheforce.
b) What is the effect of this force on the moving particle?
c) What ¡s the practical application of this effect?
d) Explain the working of a device which make use of this effect with the help of a neat diagram.
Answer:
a) Magnetic lorentz force
b) This force changes the direction of motion
c) This effect is used in cyclotron
d) Constructional Details

Cyclotron consists of two semicircular dees D₁ and D₂, enclosed in a chamber C. This chamber is placed in between two magnets. An alternating voltage is applied in between D₁ and D₂. Anion is kept in a vacuum chamber.

Working
At certain instant, let D₁ be positive and D₂ be negative. Ion (+ve) will be accelerated towards D₂ and describes a semicircular path (inside it). When the particle reaches the gap, D₁ becomes negative and D₂ becomes positive. So ion is accelerated towards D₁ and undergoes a circular motion with larger radius. This process repeats again and again.

Thus ion comes near the edge of the dee with high K.E. This ion can be directed towards the target by a deflecting plate.

Question 1.
THe S.l. unit of magnetic flux density is (March – 2015)
a) henry
b) tesla
c) Am²
d) A-m
Answer:
Tesla

Question 1.
A moving charge can produce a magnetic field. (March – 2016)
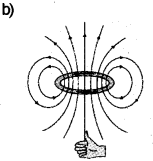
a) How does a current loop behave like a magnetic dipole?
b) Draw the magnetic field lines for a current loop to support your answer.
c) i) What is a cyclotron?
ii) Write down the expression for cyclotron frequency.
Answer:
a) A current-carrying loop has south pole at one end and north pole at another end. The magnetic field due to a circular current loop at a distance x from the centre of loop is given by

Comparing this equation with that of electric dipole, we can conclude that a current-carrying circular loop acts as a magnetic dipole.

c) i) The cyclotron is a device used to accelerate charged particle

Question 1.
A) A current-carrying conductor produces a magnetic field in the surrounding space. (Say – 2016)
a) Name the law which gives the relation between current and the magnitude of the field it produces.
OR
B) Depending on the requirement, a moving coil galvanometer can be used as a current detector, an ammeter or a voltmeter.
a) Write the principle of a moving coil galvanometer.
b) Using a suitable diagram arrive at an expres-sion for the current sensitivity of a moving coil galvanometer.
Answer:
A) a) Biot-Savarts law
OR
B) a) A current-carrying conductor experiences a torque in a magnetic field and it undergoes rotation.
b) Let I be the current flowing through the coil. When coil is placed in magnetic field B, it experiences torque τ = NAIB
where N is a number of turns and A is a cross-sectional area of coil.
This torque produces a restoring torque in the spring (kΦ, Φ is deflection) Under equilibrium
Torque on the coil = restoring torque on the spring

Φ/l is the current sensitivity. It is defined as the deflection produced by unit current.

Question 1.
a) An electric charge q is moving with a velocity v in the direction of a magnetic field B. The magnetic force acting on the charge is (March – 2017)
(i) qvB
(ii) zero
(iii) q/B
(iv) v/qB
OR
a) An ammeter is a current measuring device which is always connected in …………………. in an electric circuit.
Answer:
a) ii) zero
OR
a) Series

Question 1.
a) State and explain Ampere’s Circuital Theorem. (Say – 2017)
b) Derive an expression for the magnetic field intensity produced at a point lying along the axis of a circular coil carrying current.
OR
Explain the theory and working of a moving coil galvanometer.
Answer:
a) According to ampere’s law the line integral of the magnetic field along any closed path is equal to m₀ times the current passing through the surface.

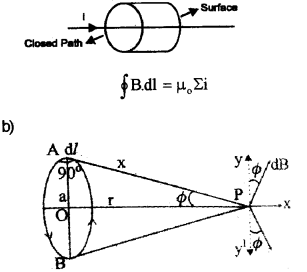
Consider a circular loop of radius ‘a’ and carrying current 9’. Let P be a point on the axis of the coil, at distance x from A and r from ‘Os. Consider a small length dl atA.

The magnetic field at ‘p’ due to this small element dl,

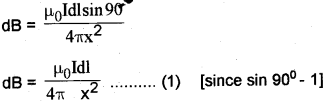
The dB can be resolved into dB coscΦ (along Py) and dB sinΦ (along Px).

Similarly consider a small element at B, which produces a magnetic field ‘dB’at P. If we resolve this magnetic field we get.

dB sincΦ (along px) and dB coscΦ (along py1) dB coscΦ components cancel each other, because they are in opposite direction. So only dB sincΦ components are found at P, so total filed at P is

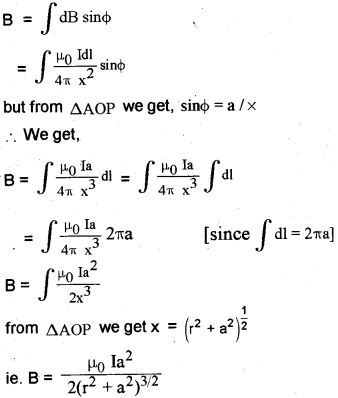
OR

It is an instrument used to measure small current.

Principe : A conductor carrying current when placed in a magnetic field experiences a force, (given by Fleming’s left-hand rule).

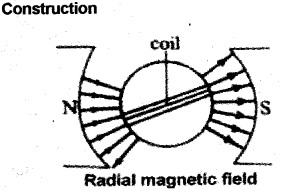
A moving coil galvanometer consists of rectangular coil of wire having area ‘A’ and number of turns ‘n’ which is wound on metallic frame and is placed between two magnets, The magnets are concave in shape, which produces radial field.

Working : Let ‘I’ be the current flowing the coil, Then the torque acting on the coil.

τ = NIAB Where A is the area of coil and B is the magnetic field.

This torque produces a rotation on coil, thus fiber is twisted and angIe (Φ). Due to this twisting a restoring torque (τ = KΦ) is produced ¡n spring.

Under equilibrium, we can write Torque on the coil = restoring torque on the spring

The quantity inside the bracket is constant for a galvanometer.
Φ α l
The above equation shows that the deflation depends on the current passing through the galvanometer.

We hope the Kerala Plus Two Chemistry Chapter Wise Questions and Answers Chapter 4 Moving Charges and Magnetism help you. If you have any query regarding Kerala Plus Two Chemistry Chapter Wise Questions and Answers Chapter 4 Moving Charges and Magnetism, drop a comment below and we will get back to you at the earliest.