Kerala Plus Two Maths Previous Year Question Paper March 2017 with Answers
| Board | SCERT |
| Class | Plus Two |
| Subject | Maths |
| Category | Plus Two Previous Year Question Papers |
Time: 2½ Hours
Cool off time : 15 Minutes
General Instructions to Candidates
- There is a ‘cool off time’ of 15 minutes in addition to the writing time of 2½ hrs.
- You are not allowed to write your answers nor to discuss anything with others during the ‘cool off time’.
- Use the ‘cool off time’ to get familiar with the questions and to plan your answers.
- Read questions carefully before you answering.
- All questions are compulsory and the only internal choice is allowed.
- When you select a question, all the sub-questions must be answered from the same question itself.
- Calculations, figures, and graphs should be shown in the answer sheet itself.
- Malayalam version of the questions is also provided.
- Give equations wherever necessary.
- Electronic devices except non-programmable calculators are not allowed in the Examination Hall.
Question 1.
a. Let R be a relation defined on A = {1,2, 3} by R = {(1,3), (3, 1), (2, 2)}.R is
a. Reflexive
b. Symmetric
c. Transitive
d. Reflexive but not transitive
b. Find fog and gof if f(x) = |x + 1| and g(x) = 2x – 1.
c. Let * be a binary operation defined on N x N by (a, b) * (c, d) = (a + c, b + d). Find the identity element for * if it exists.
Question 2.
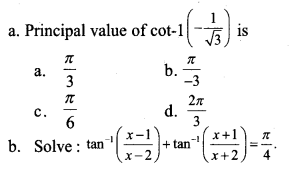
Question 3.

Question 4.
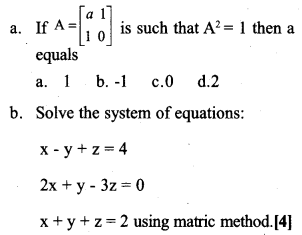
Question 5.

Question 6.
Slope of the normal to the curve y2 = 4x at (1, 2) is
a. 1
b. \(\frac { 1 }{ 2 } \)
c. 2
d.-1
b. Find the interval in which 2x3 + 9x2 + 12x – 1 is strictly increasing.
OR
a. The rate of change of volume of a sphere with respect to its radius when the radius is 1 unit
a. 4π
b. 2π
c. π
d. \(\frac { \pi }{ 2 } \)
b. Find two positive numbers whose sum is 16 and the sum of whose cubes are minimum.
Question 7.
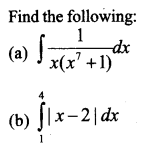
Question 8.
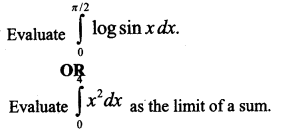
Question 9.
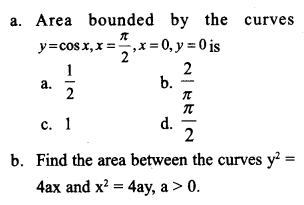
Question 10.
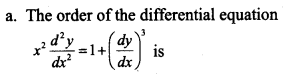

Question 11.

Question 12.
a. The angle between the vectors \(\widehat { i } \) + \(\widehat { j } \) and \(\widehat { j } \) + \(\widehat { k } \) is
(i) 60°
(ii) 30°
(iii) 45°
(iv) 90°
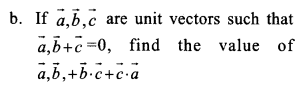
Question 13.
a. The line x – 1 = y = z is perpendicular to the line
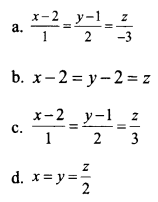
b. Find the shortest distance between the lines
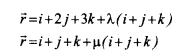
Question 14.

Question 15.
Consider the linear programming problem :
Maximize Z = 50x + 40y
Subject to the constraints
x + 2y > 10
3x + 4y < 24
x > 0, y > 0
a. Find the feasible region.
b. Find the comer points of the feasible region.
c. Find the maximum value of Z.
Maximize Z = 50x + 40y
Subject to the constraints
x + 2y > 10
3x + 4y < 24
x > 0, y > 0
Question 16.
If A and B are two events such that A ⊂ B and P(A) ≠ then P (A/B) is
a. \(\frac { P(A) }{ P(B) } \)
b. \(\frac { P(B) }{ P(A) } \)
c. \(\frac { 1 }{ P(A) } \)
d. \(\frac { 1 }{ P(B) } \)
b. There are two identical bags. Bag I contains 3 red and 4 black balls while Bag II contains 5 red and 4 black balls. One ball is drawn at random from one of the bags.
i. Find the probability that the ball is drawn is red.
ii. If the ball drawn is red what is the probability that it was drawn from the bag I?
OR
Consider the following probability distribution of a random variable X.
