Plus Two Maths Notes Chapter 7 Integrals is part of Plus Two Maths Notes. Here we have given Plus Two Maths Notes Chapter 7 Integrals.
| Board | SCERT, Kerala |
| Text Book | NCERT Based |
| Class | Plus Two |
| Subject | Maths Notes |
| Chapter | Chapter 7 |
| Chapter Name | Integrals |
| Category | Kerala Plus Two |
Kerala Plus Two Maths Notes Chapter 7 Integrals
Introduction
Integration is the reverse process of differentiation. The development of integral calculus is outcome of the efforts to solve the problems to find the function when its derivative is given and to find the area bounded by the graph of a function under certain conditions. In this chapter we study different method of find indefinite integral and definite integrals of certain functions and its properties.
A. Basic Concepts
I. Integration
Let \(\frac{d}{d x}\)F(x) = f(x). then we write ∫f(x)dx = F(x) + C.
These integrals are called indefinite integrals and C is the constant of integration.
- Indefinite integral is a collection of family of curves, each of which is obtained by translating one of the curves parallel to itself upward or downwards along the y-axis.
- ∫[f(x) ± g(x)]dx = ∫f(x)dx ± ∫g(x)dx
- For any real number k, ∫[kf(x)]dx = k∫f(x)dx
II. Some Standard Results
- ∫xn dx = \(\frac{x^{n+1}}{n+1}\) + C
- ∫\(\frac{1}{x}\)dx = log|x| + C
- ∫exdx = ex + C
- ∫axdx = \(\frac{a^{x}}{\log a}\) + C
- ∫sin x dx = -cosx + C
- ∫cos xdx = sin x + C
- ∫sec2xdx = tanx + C
- ∫cosecx cotx dx = -cosecx + C
- ∫secx tanx dx = secx + C
- ∫cosec2x dx = -cotx + C
- ∫tan x dx = log|sec x| + C
- ∫cot xdx = log|sin x| + C
- ∫sec xdx = log|sec x + tan x| + C
- ∫cosec x dx = log|cosec x – cot x| + C

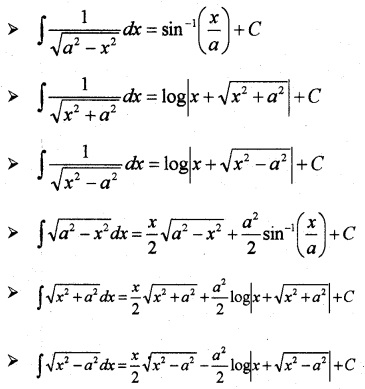
III. Some methods of Integration
1. If \(\frac{d}{d x}\) F(x) = f (x) and ∫f(x)dx = F(x) + C then ∫f(ax + b)dx = \(\frac{1}{a}\) F(ax + b) + C.
2. ∫[f(x)]n f'(x)dx = \(\frac{[f(x)]^{n+1}}{n+1}\) + C
\(\int \frac{f^{\prime}(x)}{f(x)} d x\) = log[f(x)| + C
3. ∫ex[f(x) + f'(x)]dx = exf(x) + C
4. Substitution Method:
The given integral I = ∫f(x)dx is transformed into another form by changing the independent variable x to t by substituting x = g(t). So that \(\frac{d x}{d t}\) = g'(t) ⇒ dx = g'(t)dt
∴ I = ∫f(x)dx = ∫f(g(t))g'(t)dt.
5.
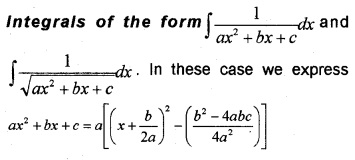
6.

7. Integration using partial fractions:
Consider Integrals of the form ∫\(\frac{P(x)}{Q(x)}\)dx, where P(x) and Q(x) are polynomials in x and Q(x) ≠ 0. If the degree of P(x) is less than Q(x), then the rational function is proper function otherwise improper function.
If \(\frac{P(x)}{Q(x)}\) is improper function, first it should be converted to proper by long division and now it takes the form \(\frac{P(x)}{Q(x)}\) = T(x) + \(\frac{P_{1}(x)}{Q(x)}\) Where T(x) is polynomial in x and \(\frac{P_{1}(x)}{Q(x)}\) is a proper function.
Now if \(\frac{P(x)}{Q(x)}\) is proper function we factorise the denominator Q(x) into simpler polynomials and decompose into simpler rational function. For this we use the following table.
8.

9. Integration by Parts:
∫f(x)g(x)dx = f(x)∫g(x)dx – ∫(f'(x) ∫g(x)dx)dx
Here the priority of taking first function and second function is more important, for this use order of the letters in words ILATE, where
- I- Inverse Trigonometric Function.
- L – Logarithmic Function.
- A – Algebraic Function.
- T -Trigonometric Function.
- E – Exponential Function.
IV. Definite Integral
A definite integral has a unique value. A definite integral is denoted by \(\int_{a}^{b}\)f(x)dx, where a is the upper limit and b is the lower limit of the integral. If \(\frac{d}{d x}\) F(x) = f(x) and ∫f(x)dx = F(x) + C , then
\(\int_{a}^{b}\)f(x)dx = F(b) – F(a).
1. Definite integral as the sum of a limit:
Let f(x) be continuous function defined on a closed interval [a, b]. Then \(\int_{a}^{b}\)f(x)dx is area bounded by the curve y = f(x), the ordinates x = a, x = b and the x-axis.
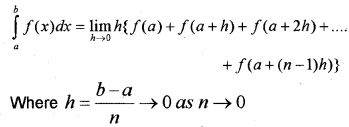
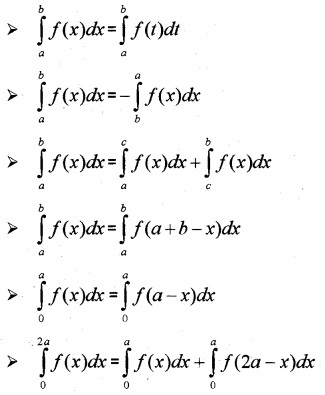
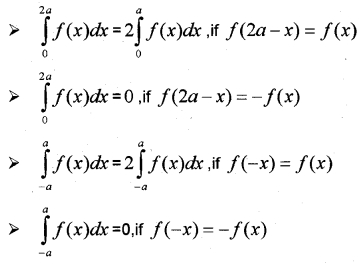
We hope the Kerala Plus Two Maths Notes Chapter 7 Integrals help you. If you have any query regarding Kerala Plus Two Maths Notes Chapter 7 Integrals, drop a comment below and we will get back to you at the earliest.