Plus Two Maths Notes Chapter 11 Three Dimensional Geometry is part of Plus Two Maths Notes. Here we have given Plus Two Maths Notes Chapter 11 Three Dimensional Geometry.
| Board | SCERT, Kerala |
| Text Book | NCERT Based |
| Class | Plus Two |
| Subject | Maths Notes |
| Chapter | Chapter 11 |
| Chapter Name | Three Dimensional Geometry |
| Category | Plus Two Kerala |
Kerala Plus Two Maths Notes Chapter 11 Three Dimensional Geometry
Introduction
To refer a point in space we require a third axis (say z-axis) which leads to the concept of three-dimensional geometry. In this chapter we study the concept of direction cosines, direction ratios, equation of a line and a plane, angle between two lines and two planes, angle between a line and a plane, shortest distance between two skew lines, distance of a point from a plane.
Basic concepts
I. Direction cosines and direction ratios
Consider a directed line passing through the origin makes angles α, β, and γ with the positive
direction x-axis, y-axis, and z-axis. Then α, β, and γ are called direction angles. The cosine of α, β, and γ are called direction cosines. Generally cos α = l, cos β = m and cos γ = n . Any scalar multiple of direction cosines are called direction ratios.
1. If (a, b, c) is the coordinate of a point P then a,b,c is a direction ratio of the directed line passing along P and origin. Direction cosines will be
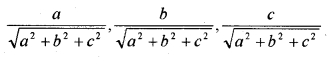
2. l2 + m2 + n2 = 1
3. Direction ratios of a line segment passing through two points(x1, y1, z1) and(x2, y2, z2) is
x2 – x1, y2 – y1, z1 – z2
4. The angle between two lines having direction ratios a1, b1, c1 and a2, b2, c2 is
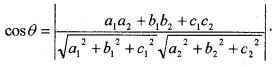
5. If direction ratios are proportional then the lines a, b, c, are parallel.ie; \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\).
6. If a1a2 + b1b2 + c1c2 = 0 then the two lines are perpendicular.
II. Line in Space
Equation of line when a point and parallel direction ratios are given:
1. Vector equation:
\(\bar{r}=\bar{a}+\lambda \bar{b}\), where \(\bar{a}\) is a point, \(\bar{b}\) is a parallel vector and λ is a parameter, for different values of λ we get parallel lines.
2. Cartesian equation:
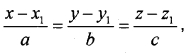
where (x1, y1, z1) is a point and a, b, c is a parallel direction ratios.
Equation of line when two points are given:
1. Vector equation:
\(\bar{r}=\bar{a}+\lambda(\bar{b}-\bar{a})\), where \(\bar{a}\) and \(\bar{b}\) are points and λ is a parameter, for different values of λ we get parallel lines.
2. Cartesianequation:

where(x1, y1, z1) and (x2, y2, z2) are two points.
Angle between two lines:
1. Vector form:
![]()
be two lines and θ be the angle between them, then cosθ =
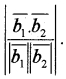
- If parallel \(\overline{b_{1}}=k \overline{b_{2}}\), k scalar.
- If perpendicular \(\overline{b_{1}} \overline{b_{2}}\) = 0.
2. Cartesian form:

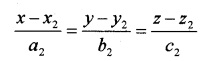
be two lines and θ be the angle between them, then
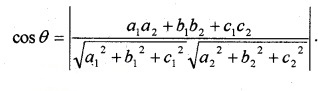
- If parallel \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
- If perpendicular a1a2 + b1b2 + c1c2 = 0.
Shortest distance between skew lines:
Lines which are neither interesting nor parallel are known as skew lines. Shortest distance between two skew lines is
1. Vector form:
![]()
be two skew lines, then d =
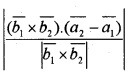
2. Cartesian form:
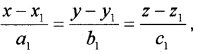
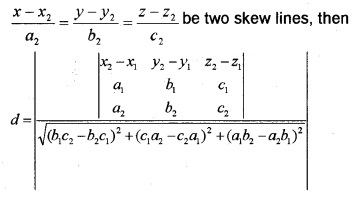
3. Distance between parallel lines,
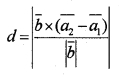
III. Plane in space
Normal Form:
1. Vector Equation:
\(\bar{r}\).\(\hat{n}\) = d, where \(\hat{n}\) is a unit vector perpendicular to the Plane, and d is the perpendicular distance of the Plane from the origin. The general vector equation of a Plane is \(\bar{r} \bar{m}=d\), where \(\bar{m}\) is any vector perpendicular to the plane and cfis a constant.
2. Cartesian equation:
lx + my + nz = d, where l, m, n are direction cosines perpendicular to the Plane and dis the perpendicular distance of the Plane from the origin. The general cartesian equation of a Plane is ax + by + cz = d, where a, b, c are direction ratios perpendicular to the plane, and d is a constant.
Equation of plane when a point and a perpendicular vector is given:
1. Vector Equation:
\((\bar{r}-\bar{a}) \bar{m}=d\), where \(\bar{m}\) is a vector perpendicular to the Plane and \(\bar{a}\) is a point on the plane.
2. Cartesianequation:
a(x – x1) + b(y – y1) + c(z – z1) = d, where a, b, c are direction ratios perpendicular to the plane and (x1, y1, z1) is a point on the plane.
Equation of a plane passing through three non-collinear points:
1. Vector Equation:
\((\bar{r}-\bar{a}) \cdot[(\bar{b}-\bar{a}) \times(\bar{c}-\bar{a})]=0\), where \(\bar{a}, \bar{b}, \bar{c}\) are points on the plane.
2. Cartesian equation:

Where, (x1, y1, z1), (x2, y2, z2) and (x3, y3, z3) are points on the plane.
3. Intercept form of the equation of a Plane:
Let a, b, c are the x-intercept, y-intercept and z- intercept made by a plane, then the equation of x y z such a Plane is \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\).
4. Angle between two Planes:
Angle between two planes is same as the angle between there perpendicular vectors.
5. Vector Form:
![]()
be two Planes and θ be the angle between them, then cos θ
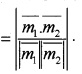
6.
(i) if parallel \(\overline{m_{1}}=k \overline{m_{2}}\), k scalar.
(ii) if perpendicular \(\bar{m}_{1} \overline{m_{2}}\) = 0
7. Cartesian form:
a1x + b1y + c1z = d1, a2x + b2y + c2z = d2 be two lines and θ be the angle between them, then
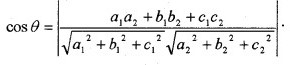
- If parallel \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
- If perpendicular a1a2 + b1b2 + c1c2 = 0
Angle between a line and a Plane:

Plane passing through the intersection of two given planes:
The equation of family of Planes passing through the intersection of the Planes a1x + b1y + c1z = d1 and a2x + b2y + c2z = d2 is a1x + b1y + c1z – d1 + λ(a2x + b2y + c2z – d) = 0.
Distance of a point from a Plane:
The perpendicular distance of the point (x1, y1, z1) from a Plane ax + by + cz = d is

The distance between parallel Planes ax + by + cz = d1 and ax + by + cz = d2 is
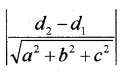
We hope the Kerala Plus Two Maths Notes Chapter 11 Three Dimensional Geometry help you. If you have any query regarding Kerala Plus Two Maths Notes Chapter 11 Three Dimensional Geometry, drop a comment below and we will get back to you at the earliest.